简单讲讲上下界网络流
无源汇可行流
无源汇网络流一般不讨论最大流,因为它的流都是环流,分布在各个位置,一是不好统计,二是一般也没有意义。所以一般建图只需要求是否有可行解(但我也没遇到过求输出YES和NO的可行流题目,网上的博客也都只当做有源汇的前置知识讲了)
废话不多说,直接上图。
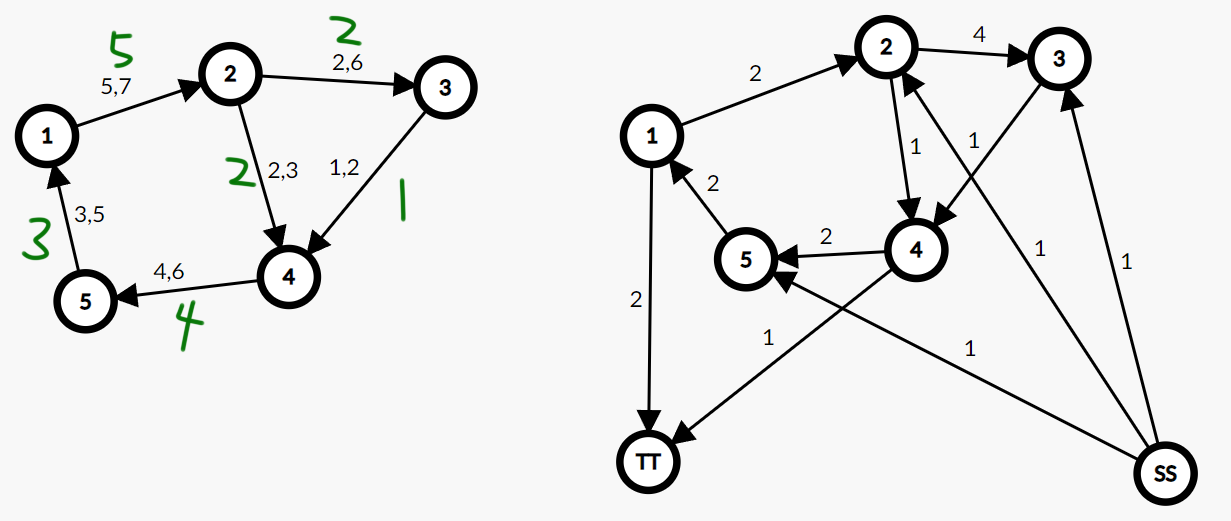
第一张图给出了无源汇模型每条边的上下界,绿色数值是每条边的下界值,即至少要流的流量。假设我们先满足下界,如果此时各个点绿色流量的流出和流入值相同,那么直接就是一个可行解,但是显然大部分情况是无法用下界来满足平衡的。我们把每条边上界减去下界的差值当做额外流量,这张图需要流一些额外流量,才能弥补之前的不平衡。
对于下界流出量大于流入量的点,之前其实没有足够的流量供它流出,所以它就需要从前面获得一些额外流量,呈现缺失态(上图点 1 和点 4);对于流入量大于流出量的点,它需要通过出边的额外流量来分掉它的流入量,呈现饱满态(上图点 2,3,5)。那么问题就变成了,能不能找到一条路线,饱满态的起点把流入它的多余流量通过这条路线转移出去,终点获得它之前缺失的流量,中间的点因为流入又流出,所以出入之差不变,这条路线的意义就是平衡了起点和终点。(路线这个概念很重要,是理解整个上下界网络流的关键,它是源汇点任意时的增广路)
我们要弥补所有点的不平衡,就要找到多条路线。具体的,先把原图两点间额外流量设成新图流量,再设置一对虚拟的源汇点,让源点向饱满态的点连一条多余流量(流入量 - 流出量)的边,让缺失态的点向汇点连一条需求流量(流出量-流入量)的边,跑从源点到汇点的最大流,如果最大流等于多余流量(或需求流量)之和,那么就是一组可行解。
初学时有一个疑问就是,饱满态的点流入量已经大于流出量了,为什么还要从源点向他连一条流入边。其实这条虚拟的流入边不是为了增加这个点的流量,而是将所有饱满态的点连在一起,方便同时找到多条增广路,新建的虚拟边流量在原图中是没有任何意义的。
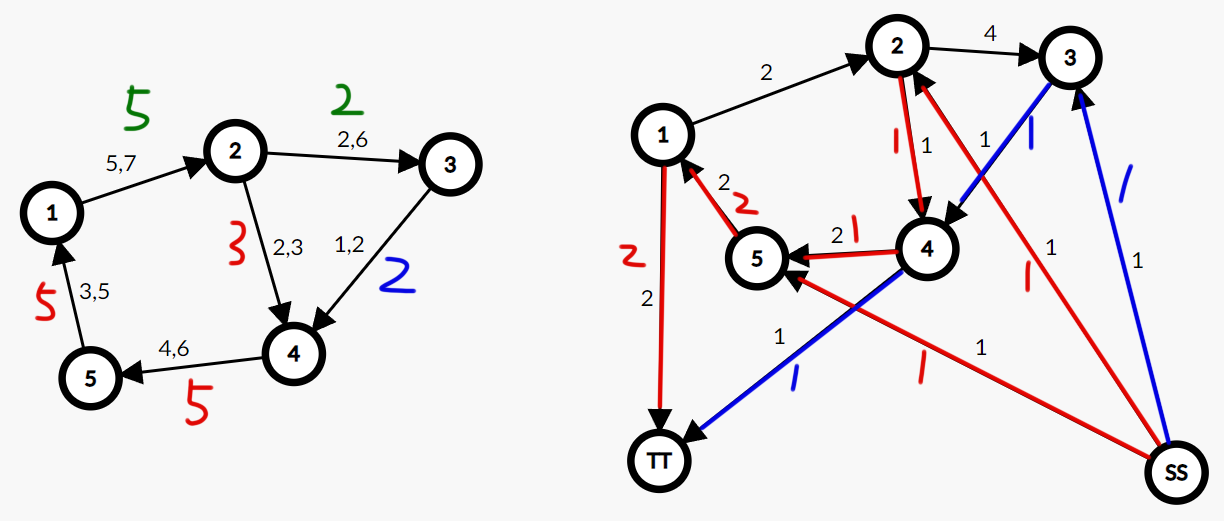
我们直接来看跑完最大流之后的情况,右图展示了新图流到汇点的两条路径,红色部分是找到了两条路线:2->4->5->1 和 5->1 各自流一个流量,蓝色部分找到了一条路线:3->4 流一个流量。在原图中的体现就是:点 2 通过原图中三条红色边的额外流量,把自己多出来的流量流回了点1 ;点 3 通过原图中蓝色边的额外流量,把自己多出来的流量流给了点 4。至此,原图的所有点流入量和流出量平衡,我们找到了一组可行流。想要输出方案也很简单,新图中每条边的流量是它原图的额外流量,加上下界,就是原图的真实流量。
有源汇上下界可行流
其实我们思考下本质,有源汇与无源汇最大的区别,除了长的样子不同,其实就是我们不再需要平衡源点和汇点的流量,虽然其他点要平衡,但源点可以是一个缺失点,只流出不流入;汇点是一个饱和点,只流入不流出。所以有源汇上下界的一个可行流,需要满足:除源点和汇点以外,其他点流入量等于流出量。
我们可以把它改造成无源汇,即从汇点向源点连一条下界为0,上界无穷的新边。不过很多博客讲有源汇上下界时没有具体讲这条边的作用,导致读者到后面理解最大流和最小流时非常困难。
在没有这条边时,我们通过找到的所有增广路,将除源汇点以外的所有点平衡流量,那么这个有源汇上下界模型就是可行的。此时只剩下流出大于流入的源点,流入大于流出的汇点。只要我们把新加的这条边,当做平衡源汇点的一条新路径,那么整张图就相当于无源汇的可行流。那么反过来,如果这张无源汇图我们知道有可行流,那么我们撤销掉新加的无穷大边的流量,原图就会变成一个除源点和汇点以外其他点流量平衡的图,即有源汇上下界可行流。
有源汇上下界最大流(最小流)
直接上图:
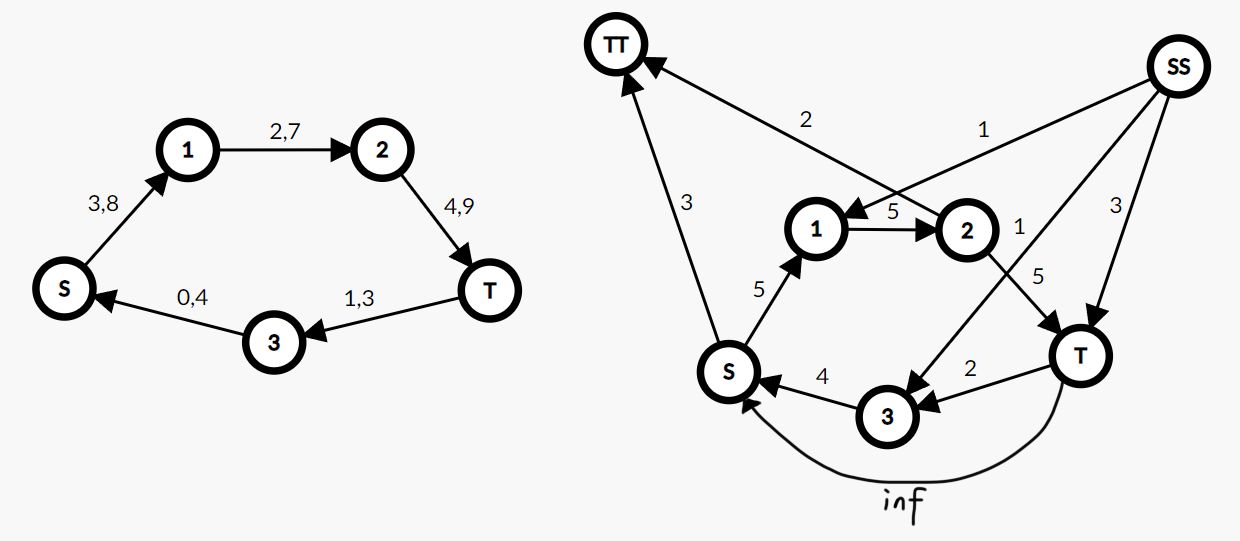
这是一个有源点和汇点的图,虽然看上去有个环,不过我们关注的还是只从源点流到汇点的最大最小流量。
求最大流的前提是,我们需要先让这张图成为可行流:发现点 3 是至少有一个流入量的,所以它一定还要向左流给源点,这一条流量会使得从源点到汇点的总体流量减一,不过没办法,因为这是成为可行流的必要流量。
在我们新建那条汇点到源点的无穷大边,并求解完一个可行流之后,我们冷静下来思考,有源汇最大流的本质是什么,其实就是在其他点流量平衡的前提下,最大化源点的缺失流量(或汇点的饱和流量)。我们还是撤销掉这条无穷大的边,那么这条边的流量,就成为了源点的缺失量,因为这条边本身的意义就是一条弥补源汇点流量差的路线(第一个标题所讲的路线)。
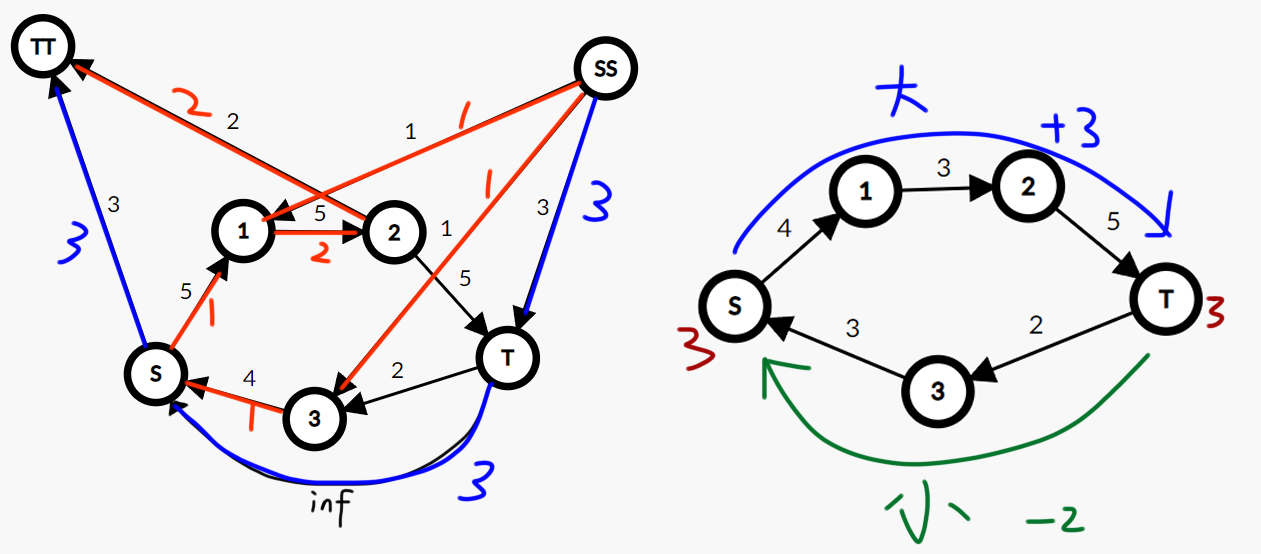
通过上图的流量,我们找到了一个可行流的解,在这个解中,无穷大的那条边流量是 2,流量平衡的过程改变了原图三条边的剩余流量。此时,如果我们撤销无穷大的边,那么源点的流入流出之差会变成 3,这其实就是一个可行流的流量。
那么聪明的你应该想到了,最大流该如何计算呢,就是在原图中,继续找到一些从源点流到汇点的路线,将源点的缺失量进一步扩大。即:s->1->2->t,流量为 3,此时源点流入流出之差为 6,为有源汇最大流。最小值则相反,找到一些从汇点到源点的路线,即:t->3->s,此时源点缺失量被弥补了一些,流入流出之差变成了 1,为有源汇最小流。
总结求解有源汇上下界最大最小流的步骤:
一、新图跑虚拟源点到虚拟汇点的最大流,判断是否有无源汇可行流。
二、将无穷大那条边的流量返还源汇点,得到有源汇可行流。
三、在原图中继续跑最大流,再加上可行流的流量(无穷大边的流量),得到答案(正着跑得到最大流,倒着跑得到最小流)。
模板:luogu东方文花帖
https://www.luogu.com.cn/problem/P5192
这题就是求个有源汇上下界最大流,很裸的模板,不过要先被传一波教才能读懂题意。
下面的代码中 a 数组存了原图的每一条边,包括上界和下界的信息。然后 solve 函数就是有源汇上下界最大流的全部过程了,包括建边,和上面总结的三个步骤。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const ll N=501010;
const ll inf=0x3f3f3f3f;
inline ll read() {
ll sum = 0, f = 1; char c = getchar();
while(c<'0' || c>'9') { if(c=='-') f = -1; c = getchar(); }
while(c>='0'&&c<='9') { sum = sum * 10 + c - '0'; c = getchar(); }
return sum * f;
}
ll n,m,s,t,ss,tt;
struct EE{ ll u,v,l,r; } a[N]; ll cnta;
ll du[N];
struct E{
ll to,nxt,cap;
}e[N];
ll cnt = 1;
ll head[N],cur[N];
ll dep[N],vis[N];
queue <ll> q;
inline void add(ll u,ll v,ll w) {
// cout<<u<<" -> "<<v<<" "<<w<<endl;
e[++cnt] = (E){ v,head[u],w }; head[u] = cnt;
e[++cnt] = (E){ u,head[v],0 }; head[v] = cnt;
}
inline bool SPFA(ll S,ll T) {
for(ll i=0;i<=tt;i++) dep[i] = inf, vis[i] = 0, cur[i] = head[i];
q.push(S); dep[S] = 0;
while(!q.empty()) {
ll u = q.front(); q.pop();
vis[u] = 0;
for(ll i=head[u]; i; i=e[i].nxt) {
ll v = e[i].to;
if(dep[v] > dep[u] + 1 && e[i].cap) {
dep[v] = dep[u] + 1;
if(vis[v]) continue;
q.push(v);
vis[v] = 1;
}
}
}
return dep[T]!=inf;
}
ll DFS(ll u,ll goal,ll flow) {
ll res = 0, f;
if(u==goal || !flow) return flow;
for(ll i=cur[u]; i; i=e[i].nxt) {
cur[u] = i;
ll v = e[i].to;
if(e[i].cap && (dep[v] == dep[u]+1)) {
f = DFS(v,goal,min(flow-res,e[i].cap));
if(f) {
res += f;
e[i].cap -= f;
e[i^1].cap += f;
if(res==flow) break;
}
}
}
return res;
}
ll solve() {
ll ans1 = 0, ans2 = 0, cha = 0;
for(ll i=1;i<=cnta;i++) {
ll u = a[i].u, v = a[i].v;
du[u] += a[i].l;
du[v] -= a[i].l;
add(u, v, a[i].r-a[i].l);
}
ll lim = cnt;
for(ll u=s;u<=t;u++) {
if(du[u]>0) add(u,tt,du[u]), cha += du[u];
if(du[u]<0) add(ss,u,-du[u]);
}
add(t,s,inf);
while(SPFA(ss,tt)) cha -= DFS(ss,tt,inf);
if(cha) return -1;
ans1 = e[cnt].cap;
for(ll i=lim+1;i<=cnt;i++) e[i].cap = 0;
while(SPFA(s,t)) ans2 += DFS(s,t,inf);
return ans1+ans2;
}
void chushihua() {
cnt = 1;
cnta = 0;
for(ll i=0;i<=tt;i++) head[i] = du[i] = 0;
}
int main() {
ll x,y,l,r;
while(scanf("%lld%lld",&n,&m)!=EOF) {
chushihua();
s = 0; t = n+m+1; ss = n+m+2; tt = n+m+3;
for(ll i=1;i<=m;i++) {
x = read();
a[++cnta] = { i+n,t,x,inf };
}
for(ll i=1;i<=n;i++) {
x = read();
y = read(); a[++cnta] = { s,i,0,y };
while(x--) {
y = read()+1; l = read(); r = read();
a[++cnta] = { i,y+n,l,r };
}
}
cout<<solve()<<"\n\n";
}
// n = 3; s = 0, t = 4; ss = 5; tt = 6;
// a[++cnta] = {s,1,2,4};
// a[++cnta] = {1,2,0,1};
// a[++cnta] = {1,3,3,5};
// a[++cnta] = {2,t,1,5};
// a[++cnta] = {3,t,1,3};
// cout<<solve()<<"\n";
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号