CF2013 D,E 题解
唉,CF的场次号马上要到2024了。
只做了 D E,两道题想明白的话,代码都相当之短。
D:
题意: 给你一个数列,你可以操作无数次,将左边数-1,右边数+1,请最小化极差。
Solution:
这题看完题发现和牛客多校那道签到题好像,不是好像,是一模一样。
所以知道做法了,不过那题是暴力风吹沙,这题 n 范围 1e5 还要用单调栈模拟,用单调栈模拟每个高度的数有几个,比较难写(相比于正解),还有些小细节:
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#define FOR() ll le=e[u].size();for(ll i=0;i<le;i++)
#define QWQ cout<<"QwQ\n";
#define ll long long
#include <vector>
#include <queue>
#include <map>
using namespace std;
const ll N=501010;
const ll qwq=303030;
const ll inf=0x3f3f3f3f3f3f3f3f;
ll T;
ll n,m;
ll ans,a[N];
ll q[N],num[N],R;
inline ll read() {
ll sum = 0, ff = 1; char c = getchar();
while(c<'0' || c>'9') { if(c=='-') ff = -1; c = getchar(); }
while(c>='0'&&c<='9') { sum = sum * 10 + c - '0'; c = getchar(); }
return sum * ff;
}
void chushihua() {
for(ll i=0;i<=n;i++) q[i] = num[i] = 0;
}
int main() {
T = read();
while(T--) {
chushihua();
n = read();
for(ll i=1;i<=n;i++) a[n+1-i] = read();
q[R=0] = inf; num[0] = 1;
for(ll i=1;i<=n;i++) {
ll now = a[i];
if(now<q[R]) {
q[++R] = now; num[R] = 1;
continue;
}
while(now>=q[R]) {
ll cha = q[R-1]-q[R];
if(R-1!=0 && (now-q[R-1] > cha*num[R])) {
now -= cha*num[R];
num[R-1] += num[R];
R--;
}
else {
ll zong = q[R] * num[R] + now;
ll ji = zong / (num[R]+1);
ll duo = zong % (num[R]+1);
ll sheng = num[R]+1 - duo;
if(!duo) {
q[R] = ji;
num[R]++;
}
else {
q[R] = ji+1;
num[R] = duo;
q[++R] = ji;
num[R] = sheng;
}
now = 0;
}
}
}
cout<<q[1]-q[R]<<"\n";
}
return 0;
}
正解代码相当之短,我们根本不用模拟风吹沙的过程。
我们最大值和最小值单独算。假设向右吹沙不是以整数为单位的,而是可以有小数。枚举可能成为最低的位置 i ,如果有多个最低位置取最右,那么这个最低的位置就是前 i 个数字的平均数(要么前 i 个位置可以平齐,要么前面有更低的位置),将所有位置取最小值。
最大值和最小值是正好相反的,你可以把数组高度全部取负数,那么风吹沙的方向从向右变成了向左。具体的,若位置 i 是最高位置,那么这个高度就是 i 后缀这些数字的平均值(或者后面有更高的位置)。
要注意我们要把小数转化为整数,求最小值时,直接除以 i 自然下取整即可,求最大值时,只要有余数答案就加一,可以让总数先加 n-i+1。
具体看代码:
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#define FOR() ll le=e[u].size();for(ll i=0;i<le;i++)
#define QWQ cout<<"QwQ\n";
#define ll long long
#include <vector>
#include <queue>
#include <map>
using namespace std;
const ll N=501010;
const ll qwq=303030;
const ll inf=0x3f3f3f3f3f3f3f3f;
ll T;
ll n,m;
ll ans,a[N],sum[N];
inline ll read() {
ll sum = 0, ff = 1; char c = getchar();
while(c<'0' || c>'9') { if(c=='-') ff = -1; c = getchar(); }
while(c>='0'&&c<='9') { sum = sum * 10 + c - '0'; c = getchar(); }
return sum * ff;
}
int main() {
T = read();
while(T--) {
n = read();
for(ll i=1;i<=n;i++) a[i] = read(), sum[i] = sum[i-1] + a[i];
ll ma = 0, mi = inf;
for(ll i=1;i<=n;i++) {
ma = max(ma,(sum[n]-sum[i-1]+n-i)/(n-i+1));
mi = min(mi,sum[i]/i);
}
cout<<ma-mi<<"\n";
}
return 0;
}
E:
题意:给你数组a,你可以随意排序,最小化 \(\sum\limits_{i=1}^n gcd(a_1,a_2,...,a_i)\)。
Solution:
本以为是一道神仙题,结果竟然是个结论题。
结论就是,让 a1 等于最小值,然后每次找一个与前面 gcd 最小的数放在后面,当 gcd 取到最小的时候后面所有位置 gcd 都不变了。
由于在 gcd 取到最小值之前每次向后添加一个数字会让最小值至少除以2,因此只需要找 log 次,每次暴力枚举复杂度也没问题。
怎么证明这就是最优解呢?要靠一个不等式:当 \(b>a\) 时, \(a+gcd(a,b)\le b\)。
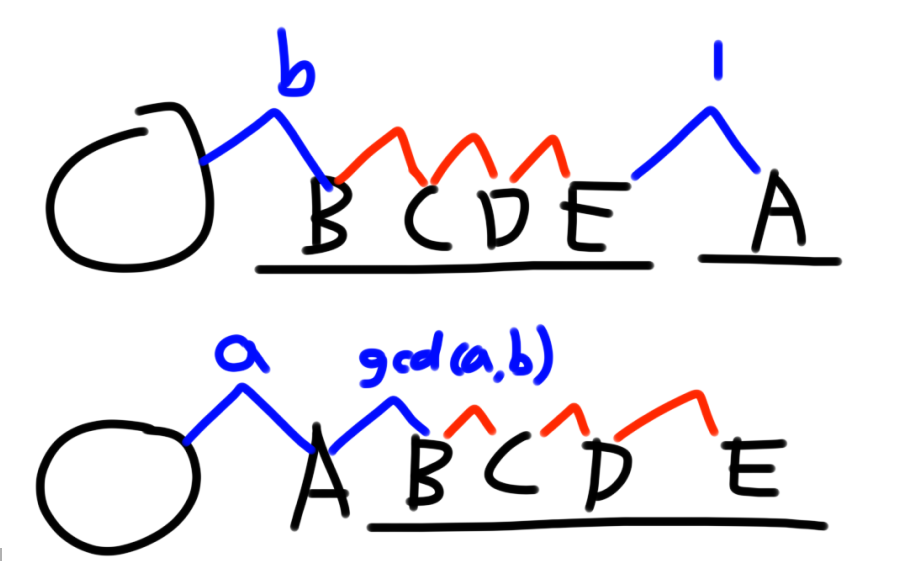
如上图,如果 A 与前面圆圈的 gcd 是 a,B 与圆圈的 gcd 是 b,若 a<b ,我们把 A 移动到 BCDE 的前面,证明下面这些位置的和小于上面。
首先红色部分下面要靠后,因此下面不超过上面;蓝色部分上方有一个 b,和最后位置,下面有一个 a,和 $gcd(pre,A,B)=gcd(a,b) $,即使上面最后一个位置是1,b 一个数字就足以让上面大于等于下面。
所以把A放前面会使整体答案变小,如果能找到更小的,继续再放 A 前面即可。贪心的策略就是这么证明的。
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#define FOR() ll le=e[u].size();for(ll i=0;i<le;i++)
#define QWQ cout<<"QwQ\n";
#define ll long long
#include <vector>
#include <queue>
#include <map>
using namespace std;
const ll N=501010;
const ll qwq=303030;
const ll inf=0x3f3f3f3f3f3f3f3f;
ll T;
ll n,m;
ll ans,a[N];
inline ll read() {
ll sum = 0, ff = 1; char c = getchar();
while(c<'0' || c>'9') { if(c=='-') ff = -1; c = getchar(); }
while(c>='0'&&c<='9') { sum = sum * 10 + c - '0'; c = getchar(); }
return sum * ff;
}
void chushihua() {
}
int main() {
T = read();
while(T--) {
chushihua();
n = read();
for(ll i=1;i<=n;i++) a[i] = read();
sort(a+1,a+n+1);
if(n==1) {
cout<<a[1]<<"\n";
continue;
}
ll gc = a[1];
for(ll i=2;i<=n;i++) gc = __gcd(gc,a[i]);
ans = gc * n;
ans += a[1] - gc;
ll now = a[1];
while(1) {
ll mi = inf;
for(ll i=1;i<=n;i++) mi = min(mi,__gcd(now,a[i]));
now = mi;
ans += now-gc;
if(mi==gc) break;
}
cout<<ans<<"\n";
}
return 0;
}
CF1614D:
这是一个和 E 题很像的题,唯一的区别就是求最小值变成了求最大值,这题就不能再用贪心结论了。
这题可以设计一个调和复杂度的 dp,还挺妙的。
设 \(cnt[i]\) 表示数组里有几个 i 的倍数,\(dp[i]\) 表示 gcd 为 i 的子序列答案最大值。\(dp[i] = MAX(dp[j]+(cnt[i]-cnt[j])*i)\) ,其中 j 是 i 的倍数。初值 \(dp[i]=cnt[i]*i\)。
easy version不需要线性筛,只要枚举倍数就能做,hard version再加些小技巧。
D1代码:
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#define FOR() ll le=e[u].size();for(ll i=0;i<le;i++)
#define QWQ cout<<"QwQ\n";
#define ll long long
#include <vector>
#include <queue>
#include <map>
using namespace std;
const ll N=5001010;
const ll qwq=303030;
const ll inf=0x3f3f3f3f;
ll n,da;
ll b[N];
ll cnt[N],dp[N];
inline ll read() {
ll sum = 0, ff = 1; char c = getchar();
while(c<'0' || c>'9') { if(c=='-') ff = -1; c = getchar(); }
while(c>='0'&&c<='9') { sum = sum * 10 + c - '0'; c = getchar(); }
return sum * ff;
}
int main() {
ll x;
n = read();
for(ll i=1;i<=n;i++) {
x = read();
b[x]++;
da = max(da,x);
}
cnt[da] = b[da];
dp[da] = da*cnt[da];
for(ll i=da-1;i>=1;i--) {
for(ll j=i;j<=da;j+=i) {
cnt[i] += b[j];
}
dp[i] = i*cnt[i];
for(ll j=2*i;j<=da;j+=i) {
dp[i] = max(dp[i],dp[j]+(cnt[i]-cnt[j])*i);
}
}
cout<<dp[1]<<"\n";
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号