二分图与网络流,ACMer需要掌握的一些模型
写在前面
前些日子的四川省赛,我们队伍拿到了网络流C题的一血。看完题目和队友讨论了下,大概两三分钟就把题目正确做法讨论出来了,但是写代码过程还是比较笨拙的,建完图后一度蒙圈甚至不知道自己建的是什么意思,后来冷静下来才把图改对。
作为23年学校图论专题的负责人,我觉得自己的网络流水平还是需要锻炼下。最近也是24暑假前集训收官了,把今年的图论专题网络流题目和以前做过的题目一起总结下。
我一直觉得,网络流题一是靠经验,二是靠一些熟悉的模型,如果模型套对了,就可以享受快速过题甚至拿一血的乐趣。
这篇随笔大概会涉及以下内容:二分图匹配、最小点覆盖、最大独立集;最小割残余网络的处理、方案的输出、切糕模型;最大权闭合子图;方阵上的一些网络流模型;DAG转二分图的模型;
讲述比较随意,可能以后还会更新。
二分图相关
二分图匹配:
点数较少的时候可以使用 \(O(nm)\) 的匈牙利算法,比较好写。
其余情况可以无脑网络流,dinic 算法跑二分图的复杂度约为 \(O(m\sqrt n)\),详见 ICPC2023济南E。
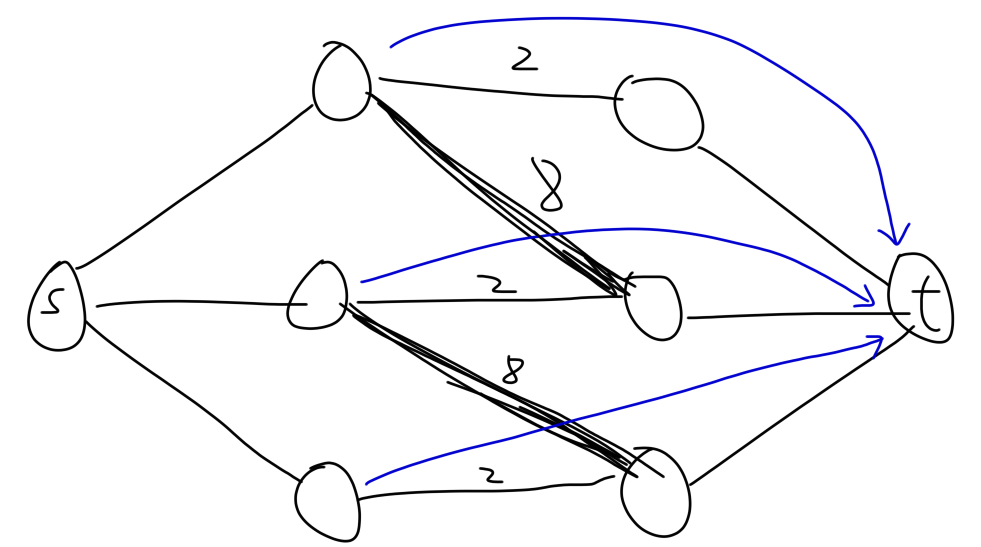
二分图最大权值匹配可以费用流,其中分为最大权匹配和最大权完美匹配,最大权完美匹配需要保证是最大流,那么直接跑最大费用最大流即可。如果没有最大匹配数的限制,最大费用最大流就不一定是最大费用流(如下图),为了让其强制最大流,可以从每个左部结点向汇点连一条费用为 0,流量为 1 的边。这个补流的思想还是比较有用的,下面会涉及到。
最小点覆盖
最小点覆盖的含义:选出图中的一些点,满足图中所有边的两端至少有一个点被选中,最小的点集即为最小点覆盖。
在二分图中,最大匹配的数量和最小点覆盖的点数是相同的。如果你将某题的题意转化为了求二分图的最小点覆盖,那么直接跑最大流就是答案。
在一般图中,最大匹配的数量和最小点覆盖的点数不一定相同,比如最简单的一个三角形图,最大匹配为1,最小点覆盖却是2。
一般图最大匹配有多项式复杂度的带花树,而一般图最小点覆盖是npc。
我们知道最大匹配的方案很好输出,匈牙利算法自动匹配好了,最大流只需要看看残余网络的情况。但最小点覆盖的方案就要稍微难找一些,Matrix67大佬的博客里有König定理的证明以及求出一组方案的过程,我们可以利用这个定理进行方案查找:二分图最大匹配的König定理及其证明
下面是匈牙利算法求最小点覆盖的代码:
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1010;
inline int read() {
int sum = 0, ff = 1; char c = getchar();
while(c<'0' || c>'9') { if(c=='-') ff = -1; c = getchar(); }
while(c>='0'&&c<='9') { sum = sum * 10 + c - '0'; c = getchar(); }
return sum * ff;
}
int n1,n2,m;
vector <int> e[N];
int vis[N],belong[N]; // index is the right_part of G(V,E)
bool tagx[N],tagy[N];
int DFS(int u) {
for(int v : e[u]) {
if(vis[v]) continue;
vis[v] = 1;
if(!belong[v] || DFS(belong[v])) { belong[v] = u; return 1; }
}
return 0;
}
void mark(int u) {
if(tagx[u]) return ;
tagx[u] = 1;
for(int v : e[u]) {
if(!tagy[v] && belong[v]) {
tagy[v] = 1;
mark(belong[v]);
}
}
}
int main() {
int x,y;
n1 = read(); n2 = read(); m = read();
while(m--) {
x = read(); y = read();
e[x].push_back(y);
}
int ans = 0;
for(int i=1;i<=n1;i++) {
memset(vis, 0, sizeof(vis));
ans += DFS(i);
}
cout<<"ans = "<<ans<<endl;
memset(vis, 0, sizeof(vis));
for(int i=1;i<=n2;i++) vis[ belong[i] ] = 1;
for(int i=1;i<=n1;i++) if(!vis[i]) mark(i);
for(int i=1;i<=n1;i++) if(!tagx[i]) cout<<i<<" ";
cout<<endl;
for(int i=1;i<=n2;i++) if(tagy[i]) cout<<i<<" ";
cout<<endl;
return 0;
}
/*
4 4 7
1 1
2 2
1 3
2 3
2 4
3 2
4 2
*/
其实除了König定理,直接在网络流的残余网络里进行DFS也可以求出最小点覆盖的方案,其过程与König定理的原理相似。
这个会在下一个大标题里讲。
最大独立集
最大独立集的含义是:选出图中的一些点,满足图中不存在两个端点都被选中的边,最大的点集即为最大独立集。
无论是在二分图还是一般图当中,最大独立集和最小点覆盖永远是互补的关系,两者相加即为总点数。证明非常简单,思考个四五秒就懂了。
也就是说,二分图的最大独立集 = 总点数 - 最小点覆盖 = 总点数 - 最大匹配。想要求二分图最大独立集点数,只需让总点数(两边点数和)减去最大流。
若要求出一组方案,那和求最小点覆盖的方法是完全相同的,因为它就是最小点覆盖的补集。
如果你可以将题目按照以下步骤转化:
1、转化为二分图,将点分成两边阵营。
2、两边阵营某些关系存在冲突(两者只能选其一),给两个点连一条边。
3、要求最大可以保留的点数。
那就是最大独立集的模型了,答案是总点数减去最小割。
二分图最小权点覆盖、二分图最大权独立集
将上面的两个对称的问题加上点权,那么最小权覆盖就是将源汇点连向中间点的边设上权值,跑最大流即为最小点权覆盖,最大权独立集可以用下面的式子算出来:
最大权独立集 = 总点权-最小点权覆盖 = 总点权-最大流
最小割的残余网络
输出最小割方案
首先总所周知,残余网络上流量为0的边,并不代表它被割掉了。因为流一次,同一条路上可能会有很多边的流量变为0,但我们只需要割一条边。
如果题目需要我们给出一组最小割的方案(例如2021 ECfinal H),我们到底应该割掉哪些边呢?
其实这是一个与最小割定义相关的问题。
最小割的定义是,将所有点划分为 S 和 T 两个集合,满足源点在 S 中,汇点在 T 中,且所有从 S 到 T 的边流量之和最小。那么,从 S 到 T 的所有边,就是我们要割掉的边。
我们跑完最大流后,为什么找不到新的增广路了,就是因为 S 到 T 的所有边都被割掉了。
如果我们从源点进行DFS,每次只沿着流量不为0的边走,我们走到的所有点的集合其实就是点集 S 的一种方案。
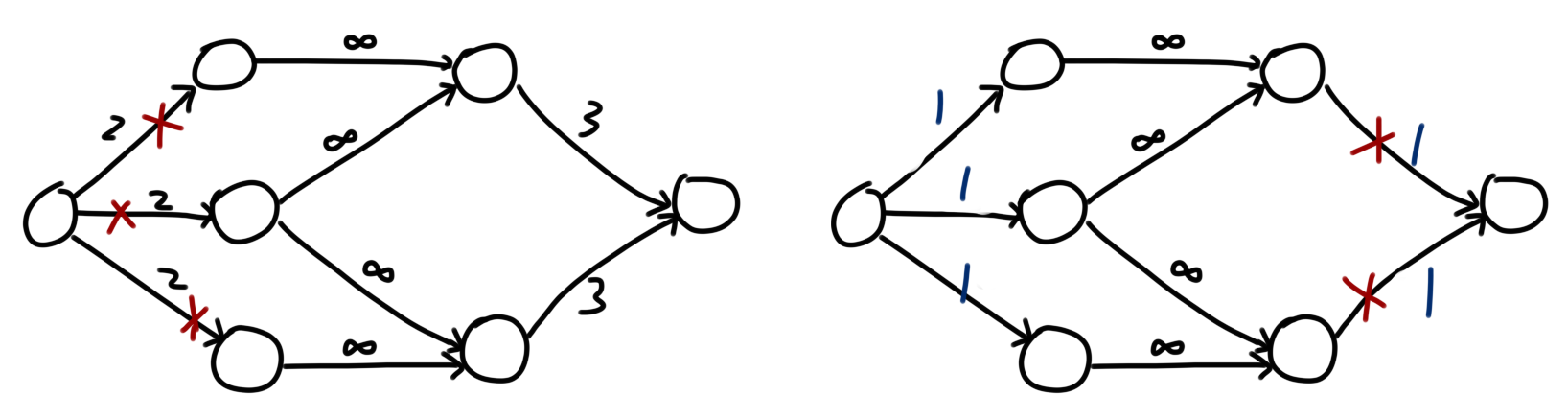
下图图一,浅蓝色边为增广路,红色为最小割的方案,虽然源点到第一个点的边流量也变成了0,但是它不能是最小割的边。
下图图二,深蓝色边是跑完最大流后的残余网络,我们从源点开始DFS,绿色点即为 S 中的点,其余点为 T 中的点。
左部点中未被绿色标记的点,是边被割去的点,右部点中被绿色标记的点,是边被割去的点。由此可以根据题意来输出一组最小割方案。
事实上,你会发现从源点开始 DFS 的过程,与 König 定理中标记点的过程非常相似。沿着未满流的原图边走,就是沿着二分图中的非匹配边走;沿着残余网络中的反向边走,就是沿着二分图中的匹配边走。图三中,红色点是最小点覆盖点集,蓝色点为最大独立集,可以发现最小点覆盖和最小割是完全一致的。也就是说,想要求最小点覆盖,实际上就是求一种最小割的方案。因此网络流图建好以后,不需要上面代码中的 mark 函数,而是直接 DFS 求出 S 点集即可。

回过来看2021 ECfinal 的 H,是让你求最多能有多少组WB交叉的2x2方块,可以根据奇偶性翻转颜色,将题意变为多少组纯白或纯黑的方块。
经过这个转化后,我们就可以套用上面提到的最大独立集的三个步骤:
纯白和纯黑的方块是两个阵营,阵营内互不影响,可以划分成一个二分图;如果两个方块有相交部分,那就不能同时满足一黑一白,因此将其左右连边;最后求出最大独立集就是最多可以留多少纯色方块。
换个方式,用最小割来理解,就是把所有冲突的路径,通过割掉左边点或者割掉右边点,使其无法形成增广路。
可以看出,最大独立集和最小割的思想是同源的。
另外从OIwiki搬来一点关于最小割方案的补充:
如果需要在最小割的前提下最小化割边数量,那么先求出最小割,把没有满流的边容量改成无穷大,满流的边容量改成1,重新跑一遍最小割就可求出最小割边数量;如果没有最小割的前提,直接把所有边的容量设成1,求一遍最小割就好了。
下面左图为原图上最小割的方案,右图为所有满流边容量改为1后的最小割方案:
切糕模型
一个比较经典的省选题,这题最小割的建图方式还是比较妙的,不过我们也可以从中提炼出一个模型来。
为什么要把切糕这题放在这里讲,因为提炼出的模型和上面的最小割方案有很大的关联。
先回顾下这题的建图方式:如果相邻两条路所切的点距离超过d,那么我们认为不满足题意,因此从一条路的下游点,向相邻路距离为d的上游点连一条边权为 inf 的边,这样如果这两条路选点距离超过d,还会存在一条额外的增广路来进行修正。(没图不好理解,具体看原题题解)
这个做法比较难想到,会让人觉得难以理解,我们换个角度进行题意转化:
相邻两条路选的两个点距离不超过d,如果我们把所有上游点向距离为d的下游点连一条新边(如下图所示),那么原题的要求就变成了:任意一条从源点到汇点的路径上,只能割一条边,求最小割。(由于源点和汇点相邻的边不会被割掉,所以每条路最上游和最下游的点不需要连新边)
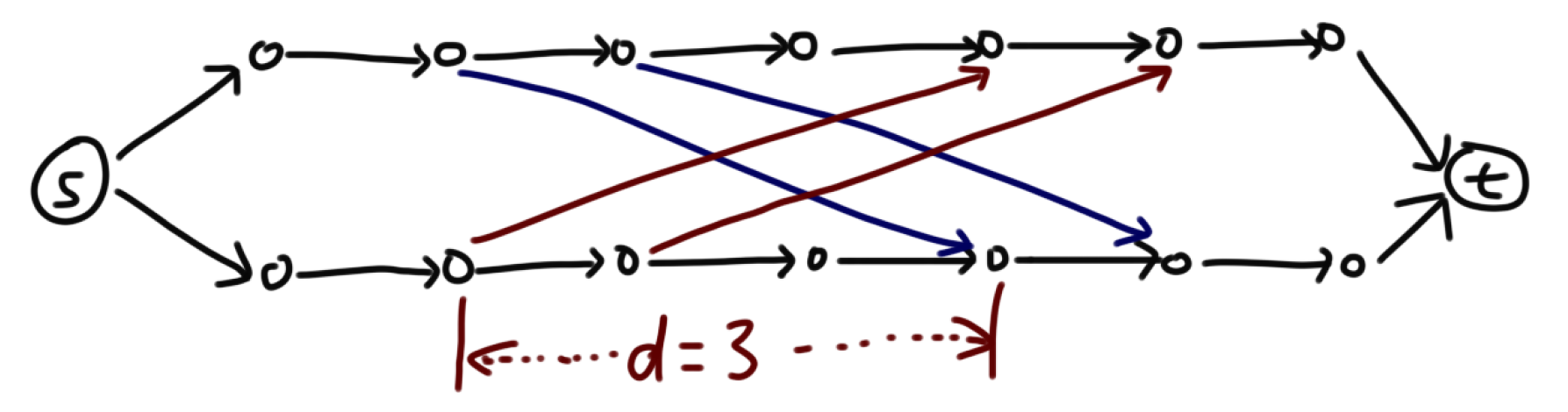
为了方便描述,我就把这个任意一条路径只割一条边的模型叫做切糕模型了。
而这个模型的解决思路也很简单:所有的边,复制一条流量为 inf 的反向边,再跑最小割就行了,求方案也是从源点DFS即可。(注意这个前提是所有的点都在源点到汇点的路径上,如果不是,去除那些无用点,再复制反向边)
关于证明,需要好几张图,我懒得画了。同校同学可以看下23年暑假前集训图论专题 Z 题的ppt题解。
简单来讲,可以考虑什么时候会出现跑完最大流后一条路上被割两条边,那一定不可能是只有一条路。在被割掉的两条边中间,一定会有一条从源点过来的路,以及一条通往汇点的路,如果中间建立了流量无穷大的反向边,就可以使源点过来的路和通往汇点的路再产生新的增广路,换一条割掉的边,使原来路径上的两条边不会同时被割掉。
其他的细节可以自行思考下。
平面图最小割
参考经典的bzoj第一题狼抓兔子。如果题目给的是一张平面图,要求出最小割,那么会有一个比较有趣的性质,就是 S 和 T 两个集合可以被一条线划分到平面的两边。
S到T的每一条边,合起来在对偶图中可以形成一条完整的路径,我们只需求出对偶图中的最短路径,就可以求出原图中最小割的方案。
另外还有一道和网络流不相干的题目:CF325D,题目大意是实时判断一个圆柱面是否被割开成上下两部分。
虽然不是网络流题目,但是也用到了 平面图最小割 转 对偶图最短路 的思想。
虽然这题是圆柱,但是可以用化环为链的思想,把圆柱展开成平面并复制一份,将上下两部分割裂开,其实就是求一条完整的路径,从左边某一个点出发,到达右边复制平面的同一个点。
ICPC2023济南E
这道题目我们需要统计新增一条边后产生增广路的情况数。
也是在残余网络上进行方案统计,不过和最小割方案不同,新增加的边不能只满足 “起点在 S 集合,终点在 T 集合”,还要满足这条边的终点能够从残余网络中到达汇点。
所以这题需要两遍DFS,一遍从源点出发走正向边,一遍从汇点出发走反向边,求出两个点集。新增加的边起点和终点在这两个点集内才算合法。
最大权闭合子图
最大权闭合子图是这样一类问题:
给出一个类似于2-sat的逻辑图,一条边 u 到 v 的含义为选了 u 这个结点,就一定要选 v 这个点。每个点有一个正权值或负权值,如何选点使得总权值和最大。(在这种逻辑图当中,选出的子图一定是闭合子图)
一般图的最大权闭合子图
这类问题并不一定是二分图,一般图的最大权闭合子图是同样的做法。
首先把点分为两个点集,正权的点放在左侧,由源点连一条流量为权值的边;负权的点放在右侧,连向汇点一条流量为负权绝对值的边;其他边正常连接,流量为无穷大。
答案为所有正权的和 - 最大流。证明略
如何输出方案呢?
其实和求最小割方案很相似,甚至更简单。
直接说结论:从源点出发沿着流量不为0的边DFS,走到的点集 S 就是答案的子图。
如果说和求最大独立集的区别,那就是最大权闭合子图不一定是二分图。
2024四川省赛C
这题要求我们使立方体满足,左下角都是黑色,右上角都是白色。
一开始我想的是切一个面,还以为是切糕模型之类的,但是贡献不是来自切断邻边,而是翻转颜色。
队友马上想到了关键的转化:如果一个点是白色,那么这个点上,右,前个方向的点都应该是白色。
我们先将所有点变成黑色点,需要一个初始的代价cost。然后如果一个点被选择,代表将这个点染白,这个点指向的所有点,也需要染白。如果一个点最初是黑色,那么将它染白需要花钱,如果一个点最初是白色,那么由黑变白其实是反悔操作,可以赚钱。赚钱的点就是最大权闭合子图中的正权点,花钱的就是负权点。一共能赚到正权和-最大流,所以最后的总花费就是cost-(正权和-最大流)。
我寻思了一下,发现cost就是正权和啊,所以最后答案直接就是最大流了。
这题还有个要求,左下角必须黑,右上角必须白,那就把这两个点单独算花费,不要连入网络流建图中。
方阵上的一些网络流模型
有很多网络流的题目是建立在方阵上的。
比如网络流24题里就有棋盘类的题目,国际象棋中,相永远走不到另一种颜色的位置上,而马每次必定会走到另一种颜色的位置上。这种天然的奇偶颜色关系,就可以建立起二分图模型。
方阵中经常会出现只有上下左右连线,没有斜边连线的情况,因此不存在奇数环,很容易让人联想到二分图的模型。
有时并不是方阵中原本的点进行建图,而是原方阵中的边,或者整体的某个块儿,视作一个点,也很容易变成网络流的模型。
这里举例说明方阵转网络流的一些模型。
2021 ECfinal H
2021 ECfinal H,还是上面那道题。
首先这个WB相间就非常迷惑人,如果想不到按照奇偶性进行颜色翻转,就很容易想偏。
在方阵平面上,相邻位置的互斥关系可以转化为网络流二分图的中间边,比如这题中,相邻的2x2方块不可能是一黑一白,存在着互斥关系。
不过这题不是单纯的将所有块儿分到二分图的两侧,因为有些方块是四个问号,既可以是白色块,也可以是黑色块。因此每个位置需要拆成两个点,左侧点表示将这个位置涂成全白,右侧点表示将这个位置涂成全黑,因此同一个位置的左右两个点也是互斥的,需要连一条边。再将其他八个方向有重叠部分的互斥关系连边。跑一个最大独立集。
CF1404E
用长条铺满方阵中要求的位置,题意就非常的网络流。
因为长条是不允许拐弯的,因此我们不允许有L型的几个位置合在一起的情况。我们把两个位置合一起的操作,看做是选择两个位置中间的点,那么不允许L型的合并,也就是不允许一个位置同时选择相邻的两个点。
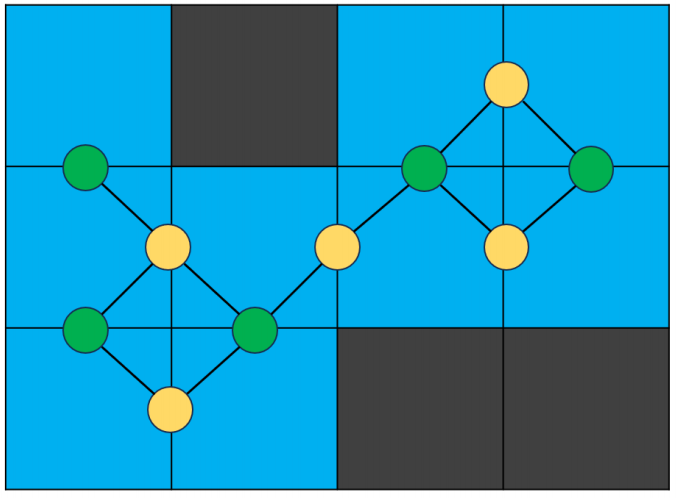
将这些有冲突的点进行连边,我们会发现由于平面的性质,它也是一张二分图,跑一个最大独立集,就是最多能进行几次合并。
每一次合并可以减低一点费用,将 '#' 的数量减去合并的最大数量为最终答案。
另外再讲一个和这题题意很像的,但正解不是网络流:江苏省赛J
题意是用一些1*k的骨牌覆盖方阵,骨牌不能重叠或者有相邻边,求最大能覆盖的权值。
骨牌没有相邻边意味着选择的所有点不能出现L型的三个点,而不能出现L型的三个点,就是任意2x2的小方块内最多选两个点。
本来以为可以建成二分图,左边点表示2x2的小方块,右边点表示每一个位置,左边点连汇点流量是2来控制方块内点数。结果发现不行,这条流量为2的边,并不能限制方块内的点数,因为这些位置也可以从其他相邻的方块找流量流进来。
目前还没想到网络流做法,估计是没法做。数据范围很小,正解是状压,不在这里讲了。
DAG转二分图
售货员问题?
先来讲一个很像售货员问题的题目:
n 个点 m 条边的 DAG,你可以花费 \(a_i\) 传送到 \(i\) ,求每个点恰好经过一次走完所有点的最小花费。
有个上下界的模型可以解决这个问题,不过没有必要,可以用按照出度入度拆点的方式将DAG转成二分图来解决。
具体的,每个点拆成左右侧两个点;由于每个点恰好经过一次,视作入度为1,每个右侧点向汇点连一条流量为1的边;每个点可以走到其他点一次,视为出度为1,从源点向左侧点连一条流量为1的边;原图中的边,从左侧点连接到右侧点,流量为1,费用为原图边权。
这时跑费用流。中间的某条边满流,说明路径中选择了这个点;连向汇点的边满流,说明这个点被到达。
现在的图最大流不是n,这是因为在没有传送时,一些点是可能无法到达的。比如这题没说一开始在DAG中的起点,而是通过传送来到DAG中,我们考虑将传送的路线加入二分图中。
通过原图中的边从 u 走到点 v ,也就是二分图左侧点 u 连向右侧点 v 的这条路;直接传送到点 v ,就是不需要花费左侧点的出度(每个点的出度只能用一次),而是直接从源点连一条到右侧点 v ,费用为 \(a_v\) 的边。
将这两种移动方式的边都连上,图就算建完了,跑费用流就是每个点经过一次的答案。
可以发现,这题中从源点连向右侧点这一个补流的操作,和上面讲到的二分图最大权匹配时的补流思想是很相似的。
最小生成树?
再讲一个很像最小生成树的问题:CF277E
平面上有一些点,每个点只能向高度小于它的点连边,且最多连出两条边,边权为两点欧几里得距离,求连接所有点的最小边权。也就是,求出一棵最小生成二叉树。
与上一个例题思路一致,我们将每个点拆成二分图左右两点,左边点代表出度,右边点代表入度。
每个点最多连出两条边,因此从源点向左边点连一条流量为2的边;每个点只有一个入度,因此右侧点向汇点连一条流量为1的边;而中间所有可以连接的边,都连一条流量为1,费用为欧几里得距离的边。
跑费用流,答案就是最小生成二叉树。
这题没有指定起点,但是默认从最高的点出发,最高的点入度为0,它不需要向汇点连边。如果最高的点不止一个,那么输出无解。如果右侧点连向汇点的边不能满流,说明也是无解,含义就是它们无法获得足够多的入边。
为什么两题都需要保证是DAG?
我们都知道售货员问题是npc的,因为这种建图的前提是DAG。
我们再来思考下两道题的路线方案:
第一题中,我们可以使用传送,传送完之后可以从落点走一条链,所有的链不重不漏覆盖所有的点。
第二题中,二叉树的第二条出边也相当于传送到了该点,并从该点开始走一条链,只不过这条链的起点挂在了以前经过的点上。
这样一来,我们的链在DAG中都是有始有终的,一个出边对应另一个点的入边。
如果DAG改成了一般图,就打破了这个平衡,我们甚至可以不使用传送,而是在二分图中跑出一个 1->2, 2->3, 3->1 的环作为费用,这样同样是满足了每个点访问一次,但是却无法找到一条进入环的路线,无论是从其他点还是传送。
第二题也不能是DAG,因为我们的建图只能保证:每个点出边上限为2,入边必须为1,但无法保证图的联通性问题。因为这两个限制在一般图中可能会以基环树森林的形式出现,即某个点出边连向了自己的祖先,从而认为祖先结点不需要从更高的祖先连边,造成图不连通。而在DAG中,只要规定了入边为1,那么一定是生成的子图一定是一棵树。
写在后面
感觉,也没什么需要写在后面的了。
就是不定期会更新吧,如果以后看到类似的模型也会丢到这篇随笔里来。
上下界可能也会做些总结,不过就不往这里丢了,这篇已经够长了。
真能看完的读者希望能有点收获吧,哪怕只是几道例题的指路也好。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号