“线段树分治+可撤销并查集”详解

参考博客：Schucking-Sattin

记录一下这个小科技。

板子题：CF1814F

题意： n个点m条边的无向图，但每个点有一个出现时间段，求哪些点满足存在某一个时刻与 1 相连。

Solution:

这个科技关注的主要是每一条边出现的时间段。但其实每个点有一个时间段，就可以推出每一条边出现的时间段，这个比较简单。

最暴力的做法就是每个时间点都做一次加边操作，加完边之后把 1 所属的连通块所有点打上标记，这是n^2。

浪费时间的有两个点：一是加边，二是给连通块的点打标记。

对于加边：我们发现一条边在某一个时刻加上了，下一个时刻可能还在，我们每次都加入这个边会很浪费时间，能不能留着它，只把那些时间结束的边删掉。

对于打标记：DFS这个连通块显然是愚蠢的，我们选择使用并查集在根部进行打标记操作。

目测就是一个可撤销并查集。

但仅仅选用可撤销并查集还不行。可撤销并查集并不是能撤销任意一条边，而是只能像栈一样撤销上一次的操作，也就是撤销最近加入的边。

如果我们每条边的时间是树状嵌套的还行，有交叉的话就变成了撤销任意一条边。

如下图，先加蓝边再加红边，那么在蓝边撤回时不满足可撤销并查集的条件，撤销的信息是无法维护的。

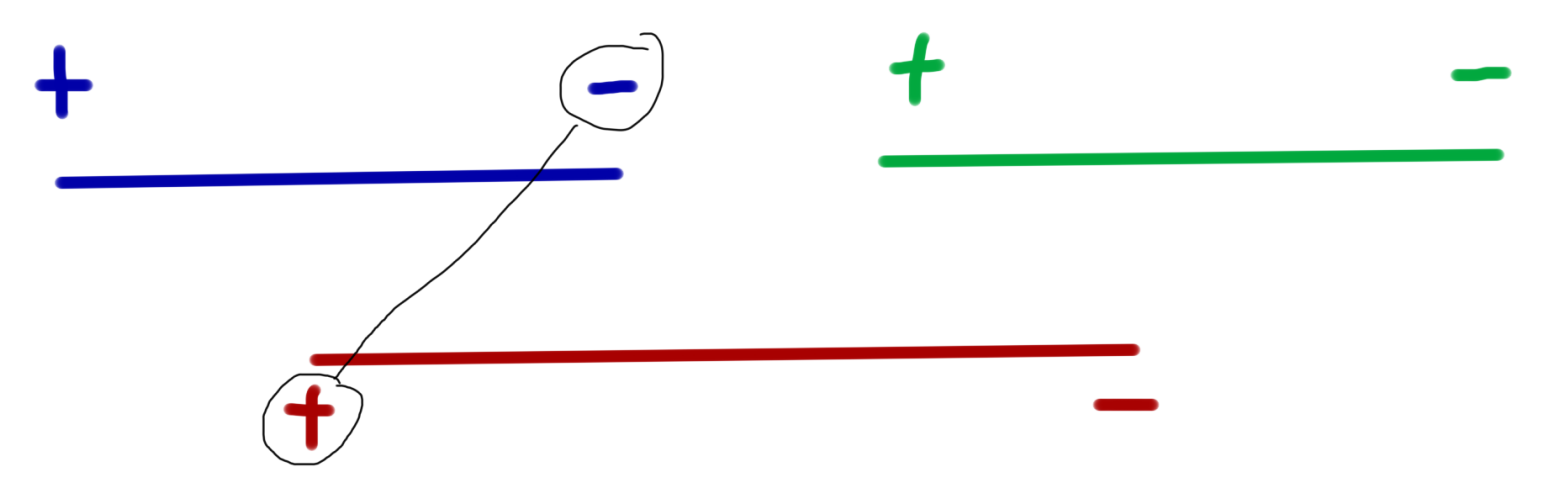
那只要我们消除时间段的交叉就可以进行撤销操作了，我们考虑把每条边的时间段切成一小段一小段，比如在每个开始或结束的地方都分段，就会变成下图情况：

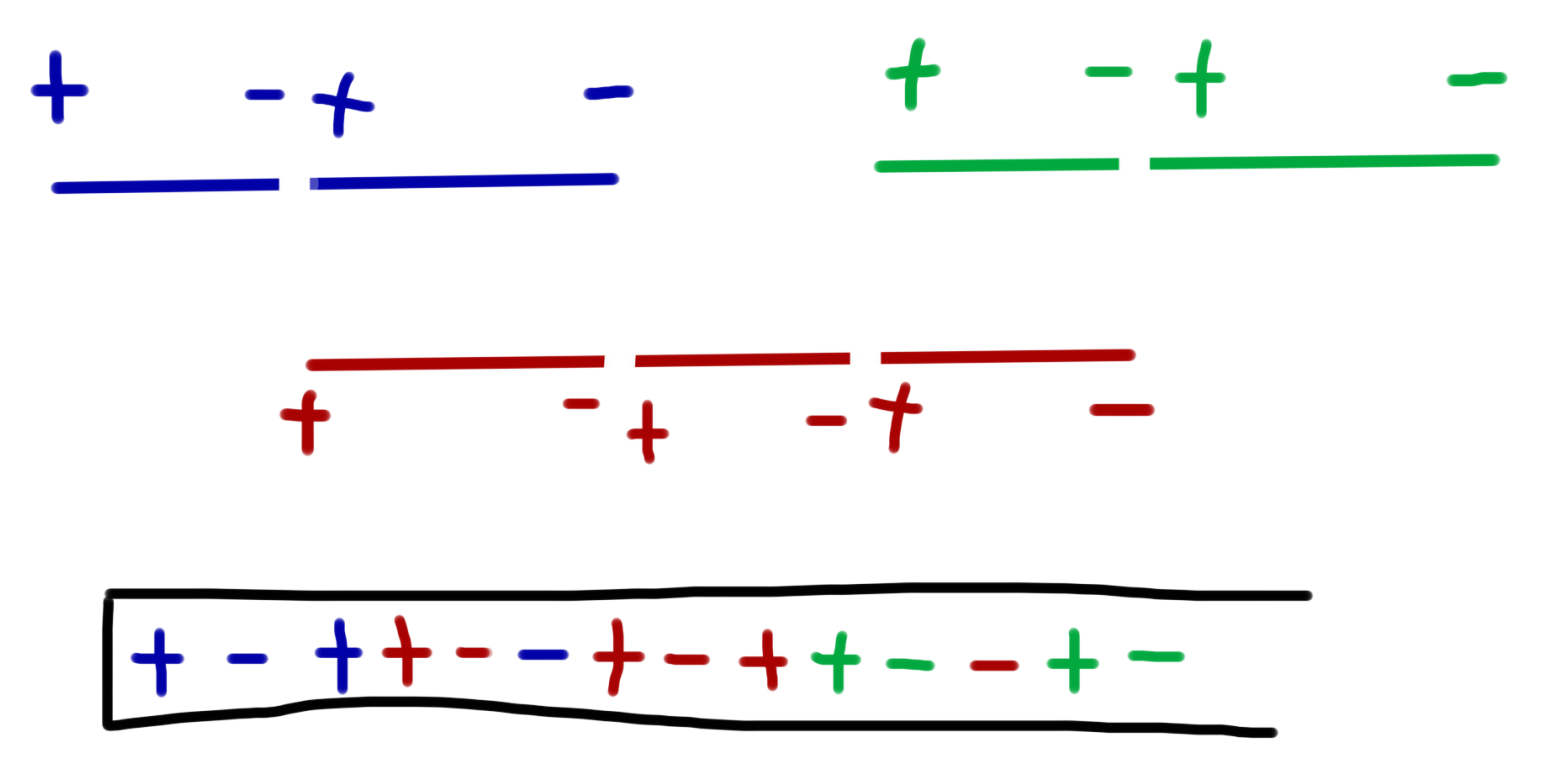
现在黑色栈里的加边和撤销操作就可以匹配上了。

但这个做法有个致命的问题就是分段太多了，最多会分 n^2 个段，可不可以少分一些。我们发现可以用线段树来减少分段量。

将每条边的时间线段用线段树来分开，每条线段只会分成log个，并且可以保证分完后的所有线段不相交。

那么回到这题的做法：

我们以时间为轴，记录线段树上每个时间区间覆盖的边，然后对线段树进行 DFS，进入一个区间就在并查集里加入这个区间的所有边，离开时再撤销这些边。

线段树分治的重点在于叶子结点，当 DFS 到叶子结点时，就是到了某个具体的时间点，我们可以对在这个时间点下的答案进行计算或者维护，我们的 DFS 可以搜索到所有的时间点。

如何用并查集维护答案，我们不能把连通块的每一个点都打上标记，我们只能对连通块的根打懒标记，而对于连通块里的其他点，我们在某条边被删除的时候，把父亲的标记下放给儿子（也就是分裂后另一个连通块的根），在所有边都分裂完之后，就能保证原来的整个连通块都打上标记。

打标记时要注意一个情况：比如我们对当前时间 1 所在的连通块根 root 打上标记，然后下一个时间 root 和 1 分离了，我们又把另一个结点 x 跟 root 连边，当 x 和 root 的边撤销时，root 会把它的标记下放给 x ，但其实 x 并没有和 1 相连。这就需要我们把每个时间点的标记分开，一个简单的做法是当 x 连向 root 时，我们先让 $tag[x] -= tag[root]$ ，以后再下放回 x 时也不会使它被打上标记。

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#define FOR() int le=e[u].size();for(int i=0;i<le;i++)
#define QWQ cout<<"QwQ\n";
#define ll long long
#include <vector>
#include <queue>
#include <map>
#define ls now<<1
#define rs now<<1|1

using namespace std;
const int N=501010;
const int qwq=303030;
const int inf=0x3f3f3f3f;

inline int read() {
    int sum = 0, ff = 1; char c = getchar();
    while(c<'0' || c>'9') { if(c=='-') ff = -1; c = getchar(); }
    while(c>='0'&&c<='9') { sum = sum * 10 + c - '0'; c = getchar(); }
    return sum * ff;
}

int T;
int n,m;
int da;
int L[N],R[N];
vector < pair<int,int> > t[N<<2];
struct CZ{
    int x,y,depy,tim;
}st[N];
int fa[N],tag[N],dep[N];
int cnt;

int find(int x) { return x==fa[x] ? x : find(fa[x]); }

void insert(int now,int l,int r,int x,int y,pair<int,int>pa) {
    if(x<=l && r<=y) { t[now].push_back(pa); return ; }
    int mid = l+r >> 1;
    if(x<=mid) insert(ls, l, mid, x, y, pa);
    if(y>mid)  insert(rs, mid+1, r, x, y, pa);
}

void merge(int x,int y,int tim) {
    int xx = find(x), yy = find(y);
    if(xx==yy) return ;
    if(dep[xx] > dep[yy]) swap(xx,yy);   //  xx -> yy
    st[++cnt] = {xx, yy, dep[yy], tim};
    fa[xx] = yy;
    if(dep[xx]==dep[yy]) dep[yy]++;
    tag[xx] -= tag[yy];
}

void DFS(int now,int l,int r) {
    for(auto v : t[now]) {
        merge(v.first, v.second, now);
    }
    if(l==r) tag[find(1)]++;
    else {
        int mid = l+r >> 1;
        DFS(ls, l, mid);
        DFS(rs, mid+1, r);
    }
    while(st[cnt].tim==now) {
        CZ cz = st[cnt--];
        tag[cz.x] += tag[cz.y];
        fa[cz.x] = cz.x;
        dep[cz.y] = cz.depy;
    }
}

int main() {
    int x,y;
    n = read(); m = read();
    for(int i=1;i<=n;i++) L[i] = read(), R[i] = read(), da = max(da,R[i]);
    for(int i=1;i<=m;i++) {
        x = read(); y = read();
        int le = max(L[x], L[y]);
        int re = min(R[x], R[y]);
        if(le<=re) insert(1, 1, da, le, re, pair<int,int>{x,y});
    }
    for(int i=1;i<=n;i++) fa[i] = i;
    DFS(1, 1, da);
    for(int i=1;i<=n;i++) if(tag[i]) cout<<i<<" ";
    return 0;
}

例题 CF1681F：

题意： 给一颗树，每条边有颜色，求 $\sum\limits_{x=1}^n\sum\limits_{y=x+1}^nf(x,y)$ ， $f(x,y)$ 表示 x 到 y 之间的路径中只出现一次的颜色数量。

Solution：

暴力很好想，如何统计每个颜色对答案的贡献，只需把树上这个颜色的边全删掉，然后累加相邻连通块大小的乘积。（顺带一提，如果题目改为 $f(x,y)$ 表示 x 到 y 之间不同颜色数量，也可以这么来统计，只需让所有点对减去路径上不包含这个颜色边的点对）

这个题的情况就和模板很相似，如果每次重新加边复杂度就是n^2，如果用可撤销并查集，需要保证每次撤销是最近的操作，而我们的做法撤销的边并不是最近加入的边。

所以我们直接套模板，颜色为 c 的边出现的时间为 $[1,c-1]$ 和 $[c+1,n]$ ，把这两个时间段拆分到线段树上。

我们线段树 DFS 到叶子结点时表示时间为 c 的状态，也就是这个颜色的边全删掉的状态。

可撤销并查集维护连通块大小，实时更新答案。

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#define FOR() ll le=e[u].size();for(ll i=0;i<le;i++)
#define QWQ cout<<"QwQ\n";
#define ll long long
#include <vector>
#include <queue>
#include <map>
#define ls now<<1
#define rs now<<1|1

using namespace std;
const ll N=501010;
const ll qwq=303030;
const ll inf=0x3f3f3f3f;

inline ll read() {
    ll sum = 0, ff = 1; char c = getchar();
    while(c<'0' || c>'9') { if(c=='-') ff = -1; c = getchar(); }
    while(c>='0'&&c<='9') { sum = sum * 10 + c - '0'; c = getchar(); }
    return sum * ff;
}

ll T;
ll n,m,da;
vector < pair<ll,ll> > t[N<<2];
vector < pair<ll,ll> > e[N];
struct CZ{
    ll x,y,depy,tim;
}st[N];
ll cnt;
ll fa[N],dep[N],siz[N];
ll ans;

ll find(ll x) { return x==fa[x] ? x : find(fa[x]); }

void insert(ll now,ll l,ll r,ll x,ll y,pair<ll,ll>pa) {
    if(x<=l && r<=y) { t[now].push_back(pa); return ; }
    ll mid = l+r >> 1;
    if(x<=mid) insert(ls, l, mid, x, y, pa);
    if(y>mid)  insert(rs, mid+1, r, x, y, pa);
}

void merge(ll x,ll y,ll tim) {
    ll xx = find(x), yy = find(y);
    if(xx==yy) return ;
    if(dep[xx] > dep[yy]) swap(xx,yy);   //  xx -> yy
    st[++cnt] = { xx, yy, dep[yy], tim };
    siz[yy] += siz[xx];
    dep[yy] += (dep[yy]==dep[xx]);
    fa[xx] = yy;
}

void DFS(ll now,ll l,ll r) {
    for(auto v : t[now]) {
        merge(v.first, v.second, now);
    }
    if(l==r) {
        for(auto v : e[l]) {
            ans += siz[find(v.first)] * siz[find(v.second)];
            // cout<<"l = "<<l<<" siz["<<v.first<<"] = "<<siz[find(v.first)]<<" siz["<<v.second<<"] = "<<siz[find(v.second)]<<"\n";
        }
    }
    else {
        ll mid = l+r >> 1;
        DFS(ls, l, mid);
        DFS(rs, mid+1, r);
    }
    while(st[cnt].tim==now) {
        CZ cz = st[cnt--];
        dep[cz.y] = cz.depy;
        siz[cz.y] -= siz[cz.x];
        fa[cz.x] = cz.x;
    }
}

int main() {
    ll x,y,z;
    n = read(); da = n;
    for(ll i=1;i<n;i++) {
        x = read(); y = read(); z = read();
        if(z!=1)  insert(1, 1, da, 1, z-1, pair<ll,ll>{x,y});
        if(z!=da) insert(1, 1, da, z+1, da, pair<ll,ll>{x,y});
        e[z].push_back( pair<ll,ll>{x,y} );
    }
    for(ll i=1;i<=n;i++) fa[i] = i, siz[i] = 1;
    DFS(1, 1, da);
    cout<<ans;
    return 0;
}

例题：P5631 最小mex生成树

题意：给一张带边权的无向连通图，求一棵生成树，其边权的mex值最小。

Solution：

其实思路和上题很像，我们把图中所有边权为 x 的边删掉，若图仍然连通，则可以构造一个生成树满足 $mex\le x$ ，因此我们找到最小的 x 即可。

并查集维护连通块大小， $size=n$ 说明全图连通。

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#define FOR() int le=e[u].size();for(int i=0;i<le;i++)
#define QWQ cout<<"QwQ\n";
#define ll long long
#include <vector>
#include <queue>
#include <map>
#define ls now<<1
#define rs now<<1|1

using namespace std;
const int N=1201010;
const int qwq=303030;
const int inf=0x3f3f3f3f;

inline int read() {
    int sum = 0, ff = 1; char c = getchar();
    while(c<'0' || c>'9') { if(c=='-') ff = -1; c = getchar(); }
    while(c>='0'&&c<='9') { sum = sum * 10 + c - '0'; c = getchar(); }
    return sum * ff;
}

int T;
int n,m,da;
vector < pair<int,int> > t[qwq<<2];
struct CZ{
    int x,y,depy,tim;
}st[N];
int cnt;
int fa[N],dep[N],siz[N];

int find(int x) { return x==fa[x] ? x : find(fa[x]); }

void insert(int now,int l,int r,int x,int y,pair<int,int>pa) {
    if(x<=l && r<=y) { t[now].push_back(pa); return ; }
    int mid = l+r >> 1;
    if(x<=mid) insert(ls, l, mid, x, y, pa);
    if(y>mid)  insert(rs, mid+1, r, x, y, pa);
}

void merge(int x,int y,int tim) {
    int xx = find(x), yy = find(y);
    if(xx==yy) return ;
    if(dep[xx] > dep[yy]) swap(xx,yy);   //  xx -> yy
    st[++cnt] = { xx, yy, dep[yy], tim };
    siz[yy] += siz[xx];
    dep[yy] += (dep[yy]==dep[xx]);
    fa[xx] = yy;
}

void DFS(int now,int l,int r) {
    for(auto v : t[now]) {
        merge(v.first, v.second, now);
    }
    if(l==r) {
        if(siz[find(1)]==n) { cout<<l-1; exit(0); }
    }
    else {
        int mid = l+r >> 1;
        DFS(ls, l, mid);
        DFS(rs, mid+1, r);
    }
    while(st[cnt].tim==now) {
        CZ cz = st[cnt--];
        dep[cz.y] = cz.depy;
        siz[cz.y] -= siz[cz.x];
        fa[cz.x] = cz.x;
    }
}

int main() {
    int x,y,z;
    n = read(); m = read(); da = 100005;
    for(int i=1;i<=m;i++) {
        x = read(); y = read(); z = read()+1;
        if(z!=1)  insert(1, 1, da, 1, z-1, pair<int,int>{x,y});
        if(z!=da) insert(1, 1, da, z+1, da, pair<int,int>{x,y});
    }
    for(int i=1;i<=n;i++) fa[i] = i, siz[i] = 1;
    DFS(1, 1, da);
    return 0;
}