CF730K:Roads Orientation Problem
网上好像没题解的样子,官方tutorial是个俄语油管视频。
题意:
给你一张无向连通图,请你给每条边定一个方向,使得 \(s\) 成为唯一源点,\(t\) 成为唯一汇点,且图中无环。
这样的话图是有一个性质的,就是从 \(s\) 出发无论怎么走都不会走环,然后最后都能到达 \(t\)。
乱搞的方式有很多,但是要么是在树上处理的时候没有搞清楚祖先和自己的关系导致产生了环,要么就是一味地消环导致有一些点孤立处理是图中源点数量不唯一。
我们考虑一个确定正确的做法:
我们随意选一条到从 \(s\) 到 \(t\) 的一条路径,将路径上的边定向,并放入“已定向”集合 (后面证明路径选取的先后顺序是不影响答案的)。
每次我们可以再寻找一条集合外的路径,这条路径满足从“已定向”集合连接的某个点出发,回到集合中的另一个点,起点和终点不能是同一个点否则会产生环。这样类似于河道分流之后再汇聚,由于集合中边的方向是已知的,所以这条路径的方向是确定的。我们每次拓展一条新的路径,然后给这条路径定向并加入集合,最后的结论就是,拓展完所有满足的路径之后,如果还有未被定向的边则无解。
那些未被定向的连通块,只有一种可能,就是与“已定向”集合只有一个交点,我们把这个连通块称为孤立的连通块。要么是一条线伸出去回不来,要么是回来了但是起点终点重合,这种路径只要一条边出一条边进就会产生环。原图也是只要存在这么一个孤立的连通块就无解,和割点还不太一样,因为我们是先把s和t连起来之后再去检查孤立的连通块。
那么现在证明路径选取顺序与答案无关:如果原图有解,说明没有孤立的连通块,那么一定可以通过不断地扩展路径,使得每一条边被定向。如果原图无解,说明至少有一个孤立连通块,但我们的路径从开始到最后也一直无法选到那些连通块,不存在误判有解的情况。
给张图吧:(除了s和t两个点用圆圈画出来了,其他的圈都表示环,绿色是可扩展的路径,红色是孤立连通块)
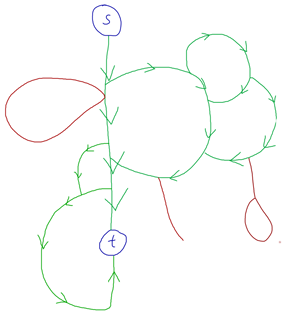
接下来是如何实现:
先从 \(s\) 出发建出来DFS树,虽然我们对DFS树习以为常,但这个树和随便生成的树不一样的地方在于:它只有树边和返祖边,没有横穿的边。
我们让t跳父亲跳到根,这条路径可以被定向了,然后我们考虑去拓展其他路径,因为所有的路径起点和终点必须在我们已定向的区域,我们发现一个性质:新拓展的路径一定是一条返祖边加上一段树上的边,画画图就看出来了。那我们就从集合中的点出发沿着返祖边下去,再爬树边到集合中另一个点,只需要记录爬树的时候定向是向下还是向上。
那么有一个小问题就是那些起点终点一样的孤立环,也是返祖边下去再树边爬上来, 我们不能去定向这些孤立环,那我们就得保证爬上来遇到的集合点和我们沿返祖边下去的出发点不是同一个点。一开始我是想通过枚举并加上倍增来判断的,后来发现不合法的情况可能会被枚举好多遍TLE掉,就参考了网上的代码,改成了一个很妙的写法:每条边记录父亲连接的返祖边(还要满足这个返祖边下面的点属于这条边的子树),只要这条边到了集合中,我们就可以从父亲出发访问那些返祖边,每条边只被访问一次,复杂度正确。
代码奉上,底下附赠两个debug样例:
#include <bits/stdc++.h>
#define QWQ cout<<"QwQ"<<endl;
#define ll long long
using namespace std;
const int N=501010;
const int qwq=2003030;
const int inf=0x3f3f3f3f;
inline int read() {
int sum = 0, ff = 1; char c = getchar();
while(c<'0' || c>'9') { if(c=='-') ff = -1; c = getchar(); }
while(c>='0'&&c<='9') { sum = sum * 10 + c - '0'; c = getchar(); }
return sum * ff;
}
int T;
int n,m,s,t;
int head[N], nxt[qwq], to[qwq], cnt=1;
bool cho[N];
int vis[N];
int fa[N],dep[N],lnk[N],son[N];
vector <int> g[N];
//lnk (edge on tree) down
//g (edge not on tree) up
void chushihua() {
for(int i=1;i<=n;i++) vis[i] = head[i] = dep[i] = fa[i] = lnk[i] = 0, g[i].clear();
for(int i=1;i<=cnt;i++) nxt[i] = to[i] = cho[i] = 0;
cnt = 1;
}
void add(int u,int v) {
nxt[++cnt] = head[u]; head[u] = cnt; to[cnt] = v;
nxt[++cnt] = head[v]; head[v] = cnt; to[cnt] = u;
}
void DFS(int u,int f) { fa[u] = f; dep[u] = dep[f] + 1;
for(int i=head[u];i;i=nxt[i]) {
int v = to[i];
if(v==f) continue;
if(dep[v] && dep[v]<dep[u]) g[son[v]].push_back(i);
else if(!dep[v]) lnk[v] = i, son[u] = v, DFS(v,u);
}
}
void search(int u,int cl) {
int now = u;
while(!vis[u]) {
if(cl) cho[lnk[u]^1] = 1;
else cho[ lnk[u] ] = 1;
vis[u] = 1;
u = fa[u];
}
while(now!=u) {
for(int i=0;i<g[now].size();i++) {
int e = g[now][i];
if(cl) cho[ e ] = 1;
else cho[e^1] = 1;
search(to[e^1],cl^1);
}
now = fa[now];
}
}
int main() {
int x,y;
T = read();
while(T--) {
chushihua();
n = read(); m = read(); s = read(); t = read();
for(int i=1;i<=m;i++) {
x = read(); y = read();
add(x,y);
}
DFS(s,0);
vis[s] = 1;
search(t,0);
bool flag = 1;
for(int i=1;i<=m;i++) {
if(!cho[i*2] && !cho[i*2+1]) { flag = 0; break; }
}
if(!flag) cout<<"No\n";
else {
cout<<"Yes\n";
for(int i=1;i<=m;i++) {
if(cho[i*2]) cout<<to[i*2+1]<<" "<<to[i*2]<<"\n";
else cout<<to[i*2]<<" "<<to[i*2+1]<<"\n";
}
}
}
return 0;
}
/*
2
5 5 1 5
1 2
2 3
3 4
4 2
2 5
9 11 1 3
2 8
4 6
5 9
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
no
yes
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号