第四次作业-树

1.学习总结

1.1树的思维导图

 

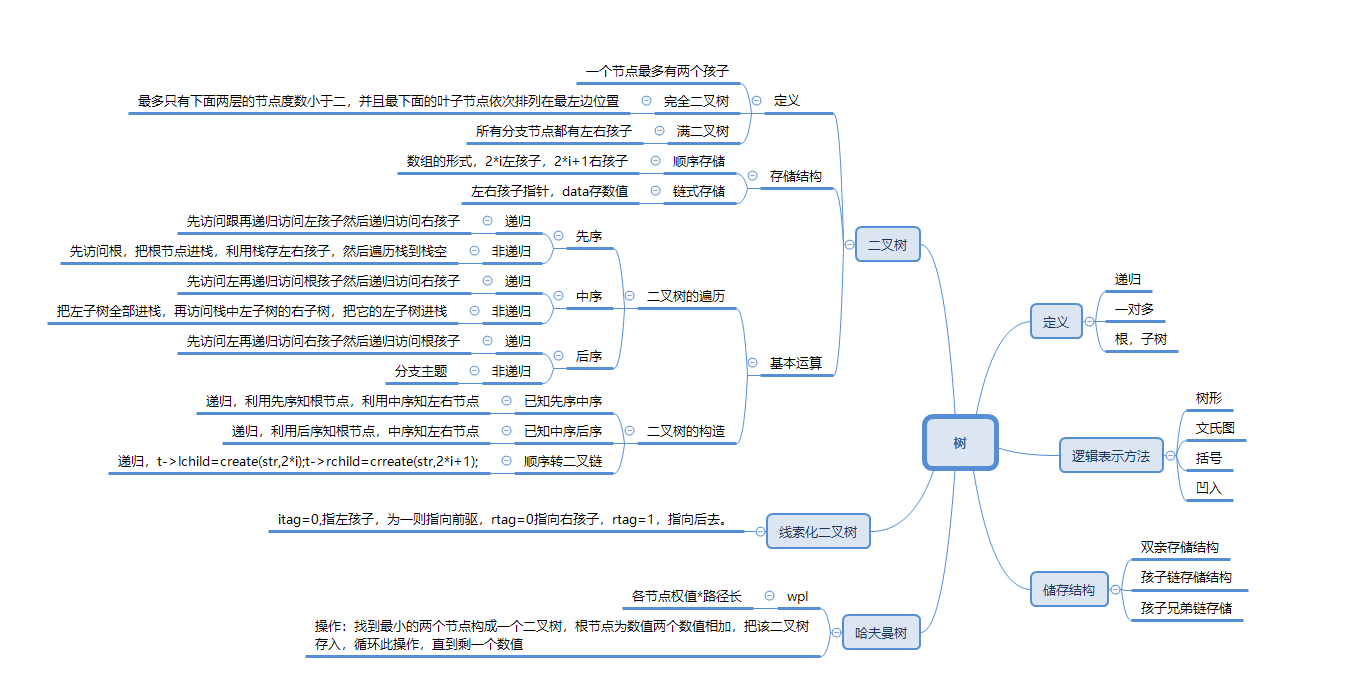
1.2 树结构学习体会

结点：存储数据元素和指向子树的链接，由数据元素和构造数据元素之间关系的引用组成。 
孩子结点：树中一个结点的子树的根结点称为这个结点的孩子结点。 
双亲结点：树中某个结点有孩子结点(即该结点的度不为0)，该结点称为它孩子结点的双亲结点，也叫前驱结点。 
兄弟结点：具有相同双亲结点(即同一个前驱)的结点称为兄弟结点。 
结点的度：结点所有子树的个数称为该结点的度。 
树的度：树中所有结点的度的最大值称为树的度。 
叶子结点：度为0的结点称为叶子结点，也叫终端结点。 
分支结点：度不为0的结点称为分支结点，也叫非终端结点

树的深度：树中结点的最大层次数，图中树的深度为4

2.PTA实验作业

Ⅰ.题目6-1 jmu-ds-二叉树操作集

2.1.1 设计思路（伪代码或流程图）

创建树
{
    定义树T
    定义i=0用来计数
    定义队列Q用来存放树的节点  
    当str[i]!=0
    {
        BT申请空间
        将str[i]赋予BT->data
        初始化左右孩子
        BT节点入队
    }
    否则 重新进入函数
    BT=NULL
    while队列Q不为空
    {
        将队头元素赋给树T
        元素出队
        如果str[i]=='#'||str[i]=='0'
            令左孩子为空
        否则
        {
            给T的左子树申请空间
            将str[i]赋给左孩子
            初始化左子树的左右孩子
            T的左孩子入队 
        }
        i++;
        如果str[i]=='#'||str[i]=='0'
            T的左孩子初始化
        否则
        {
            给T的右子树申请空间
            将str[i]赋给右孩子
            初始化右子树的左右孩子
            T的右孩子入队 
        }
        i++; 
    }
}

2.1.2 代码截图

 

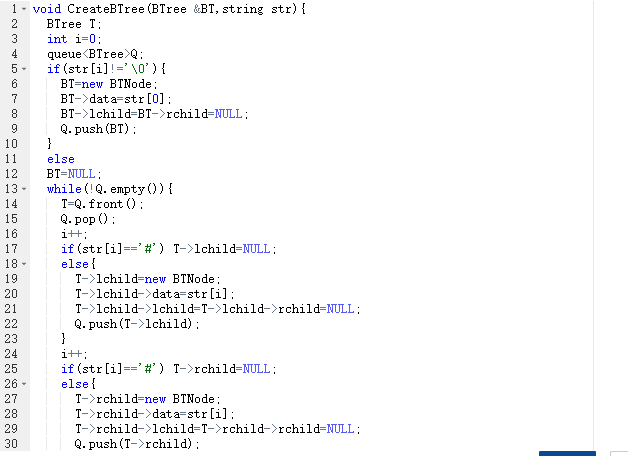
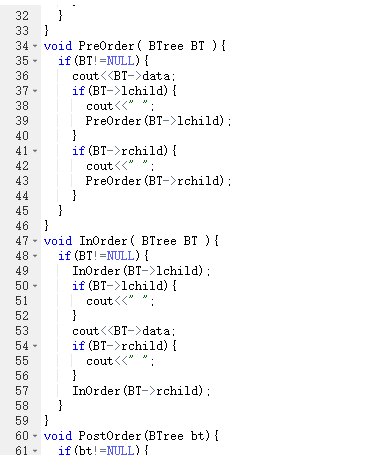
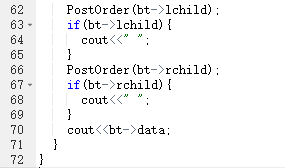
2.1.3 PTA提交列表说明。

 

说明：在同学的指导下一遍通过。

Ⅱ.题目6-4 jmu-ds-表达式树

2.2.1 设计思路（伪代码或流程图）

函数：建表达式的二叉树
定义栈s BTree
栈 char op
# 入栈op
定义i=0
while(str[i]不为‘/0’){
    当str[i]不是运算符{
        给树的节点T申请空间
     值为str[i++]
     令T的左右子树为空
     T入栈S
     }
    否则{
        switch(比较op.top(),str[i]的优先级){
       当返回 '<':
             入栈(str[i])->op;
             i++;
             break;
       当返回 '=':
             取栈顶
             i++;
             break;
       当返回 '>':
             T=new BTNode;
             T->data=op栈顶元素
             T->rchild=s栈顶元素
             s出栈
             T->lchild=s栈顶元素
             s出栈
             T入栈S
             op出栈
             break;
     }
    }
}
while(op栈顶元素不为#)
    {
        T=new BTNode;
        T->data=op栈顶元素
        T->rchild=S栈顶元素
        S出栈
        if(S不为空)
        {
            T左孩子等于s栈顶元素
            s出栈
        }
        T入栈S
        op出栈
    }
    T为s栈顶元素
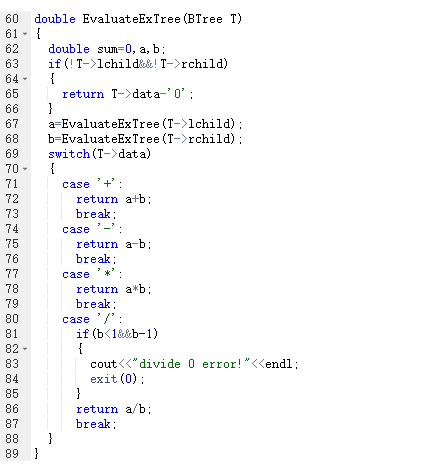
函数:计算表达式树
定义 sum=0,a,b
当T的左右子树都不为空时{
返回 T->data-'0'
}
a=递归计算左子树
b=递归计算右子树
switch(T->data)
{
   + return a+b break
   - return a-b break
   * return a*b break
   / 
   当b<1且b-1不为0{
      输出  "divide 0 error!"

   }
      return a/b
      break
}

2.2.2 代码截图

 

2.2.3 P

 

TA提交列表说明。

说明：前面少打了一个括号，一直没有发现。后面多打了一个空格，改正后正确。

Ⅲ.题目7-7 修理牧场

2.3.1 设计思路（伪代码或流程图）

定义顺序为由小到大的优先队列L

定义整形变量 n,a,i
    cin n
    for ( i=0 i<n  i++){
        cin a
        a入队
    }
    定义 sum为0;
    while(l的长度不为1){
        定义x 将队头元素值赋给x
        出队
        定义y 将队头元素值赋给y
        出队
        sum+=x+y;
        x+y入队
    }
    输出sum
    return 0;

2.3.2 代码截图

 

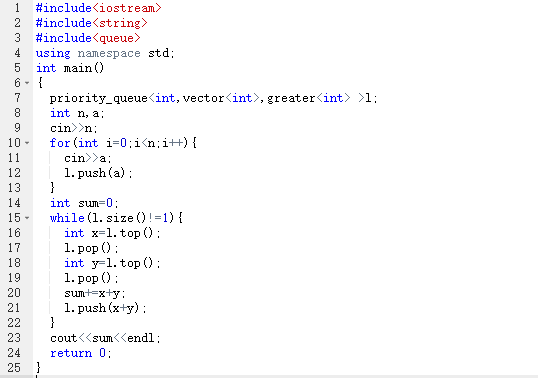
2.3.3 PTA提交列表说明。

 

说明:第一次没有改成c++，后面函数出现错误，在同学帮助下改正，后面少打了一个endl错误，改正正确。

3.截图本周题目集的PTA最后排名

PTA排名截图：

我的总分：2.5分

4. 阅读代码:

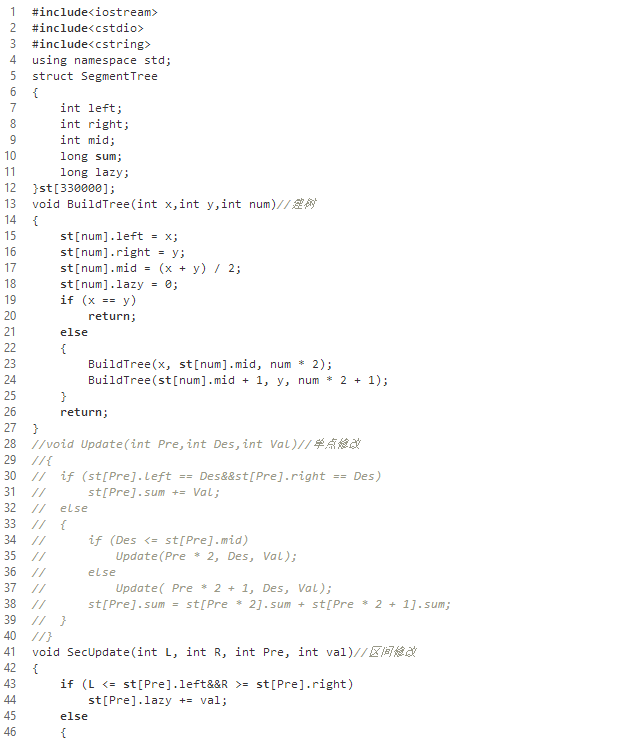
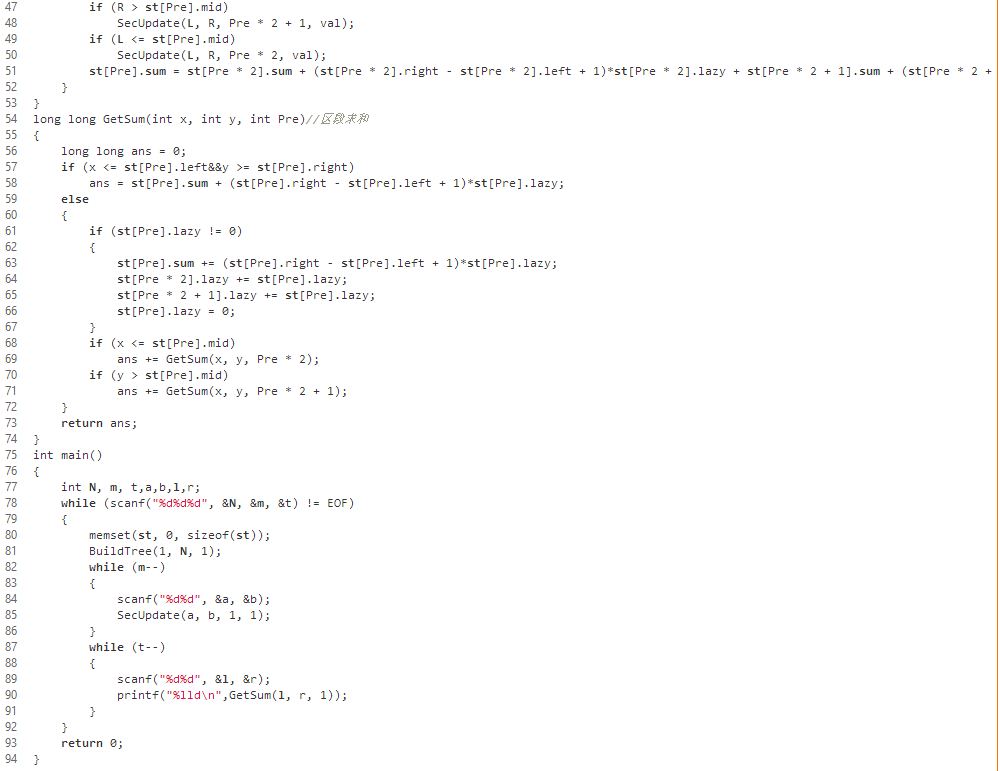
说明：这是一个线段树的代码

地址：https://gitee.com/penguinszhang/codes/th4nqorydmx9l2fjv1sc834

5. 代码Git提交记录截图