<学习笔记> 数论
-
筛法
- 欧拉函数
- 逆元
- gcd、lcm、exgcd
- 快速幂
- 矩阵乘法
- 排列组合
- 分解质因数
1.筛法：
埃式筛 O( nloglogn )
1 void Shaifa() 2 { 3 for(int i=2;i<=N;++i) 4 { 5 if(!pim[i]) 6 { 7 q[++cnt]=i; 8 for(int j=i*i;j<=N;j+=i) 9 pim[j]=1; 10 } 11 } 12 }
欧拉筛（线性筛） O ( n )
1 void Shaifa() 2 { 3 for(int i=2;i<=N;++i) 4 { 5 if(!pim[i]) q[++cnt]=i; 6 for(int j=1;j<=cnt&&(i*q[j])<=N;++j) 7 { 8 pim[i*q[j]]=1; 9 if(i%q[j]==0) 10 break; 11 } 12 } 13 }
2.欧拉函数：
φ（n）表示n的欧拉函数，对任意正整数n，欧拉函数是小于或等于n的正整数中与n互质的数的个数。（1也算）（注意φ(1)=1）。（互质：公约数只有1）
欧拉函数的简介：
其中的每种质因数只算一个，如 Φ（12）=12*（1-1/2）*（1-1/3）。
，因为除了p的倍数外，其他数都跟n互质。（p的倍数一共有 p^（k-1）个，1*p ,2*p...p^（k-1）*p）;
。特殊性质：当n为奇数时，
, 证明与上述类似。
。
公式证明：
1.容斥定理
设p1,p2,p3...pm为n的质因子，则n的欧拉函数为n减去包含p1的不超过n的数的个数，减去包含p2的不超过n的数的个数，再加上包含p1和p2的质因子的个数。
得到公式：
化简得到
变形
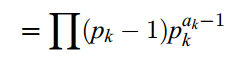
2.中国剩余定理（摘自百度百科）
根据欧拉函数的性质，我们可以在线性的时间内筛出1~n中的每个数的欧拉函数值。
线性筛欧拉函数值：
前提：
我们知道当n为质数p的k次幂(k>1)时，有Φ( n )= Φ(p^k)= p^k-p^(k-1) = (p-1)*p^(k-1),则 Φ(p^(k-1)) 即为 (p-1)*p^(k-2)。所以 Φ(p^k)=Φ(p^(k-1))*p; 我们知道对于一个任意的数都能表示为一个p^k*a的形式（p^k 与 a 互质），根据欧拉函数的积性，Φ((p^(k-1)*a)*p)=Φ(p^k*a)=Φ(p^k)*Φ(a)=Φ(p^(k-1))*Φ(a)*p=Φ( p^(k-1)*a)*p;
令 p^(k-1)*a为x，则 Φ（x*p）=Φ(x)*p;
所以对于一个质数p和正整数x，若p为x的约数，则 Φ（x*p）= Φ(x)* p;
若p不为x的约数，根据积性,有 Φ(x*p)= Φ(x)*Φ(p)=Φ(x)*(p-1);
令 phi[n]表示n的欧拉函数，可以得到代码：
1 int cnt,N; 2 int phi[100010],pim[100010],can[100010]; 3 4 void Done() 5 { 6 phi[1]=1; 7 for(int i=2;i<=N;++i) 8 { 9 if(!can[i]) pim[++cnt]=i,phi[i]=i-1; 10 for(int j=1;j<=cnt&&(i*pim[j])<=N;++j) 11 { 12 can[i*pim[j]]=1; 13 if(i%pim[j]==0) 14 { 15 phi[i*pim[j]]=phi[i]*pim[j]; 16 break; 17 } 18 else phi[i*pim[j]]=phi[i]*(pim[j]-1); 19 } 20 } 21 }
3.逆元（乘法逆元）
若 ax≡1(mod p)，则a和x互为模p意义下的逆元。
一般应用，除法取模时把 a/b(mod p)转化为 a*(1/b)(mod p).
（1）费马小定理
可知 a*a^(p-2)≡1(mod p) , a^(p-2)≡ 1/a (mod p)。
（2）欧拉定理
若 a，p都为正整数，且a,p互质，则
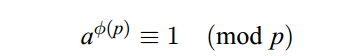
（3）exgcd
ax≡1(mod p)可转化为 ax+py=1，再求x，条件：a，p互质
（4）公式
a/b(mod p)= a(mod)(pm)/b 。
证明：
(a/b）mod m = ans ；
a/b = ans + k * m ；
a = ans * b + k * m * b ；
a mod ( bm ) = ans * b ；
a mod ( bm ) / b = ans ；
得证。
4.gcd、lcm、exgcd
（未完待续qwq。。。）
