<学习笔记> 查分约束系统
定义:如果一个系统由n个变量和m个约束条件组成,形成m个形如 ai - aj ≤ k 的不等式(i,j∈[1,n],k为常数),则称其为差分约束系统(system of difference constraints)。亦即,差分约束系统是求解关于一组变量的特殊不等式组的方法。
栗子:给出这样的一组不等式
A-B < = 3
B-C < = 6
C-D < = 5
E-C < = 2
B-E < = 3
求A-D的最大值。
经过一番脑跑之后,得出答案13。但是我们不能总是脑跑啊。。。费脑子QAQ,所以有什么科学的求法吗??
我们对A-B < = 3进行移项,改为 A < = B + 3 ,发现类似于最短路中的不等式 de[t] < = de[f] + d ,可以看做是从B到A连了一条权值为3的边。我们把上面的不等式画成图。
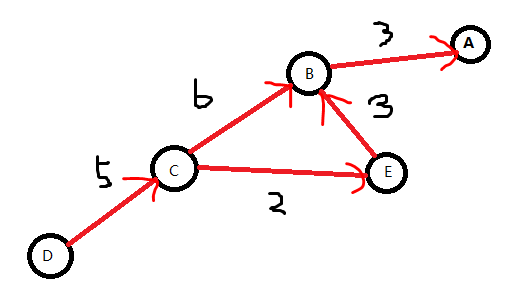
发现答案即为D到A的最短路。
为什么呢??
把图单个剥离出来看
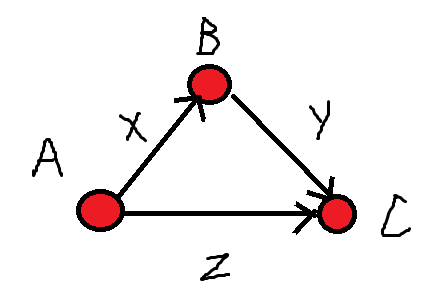
已知 (1) B-A < = x ;(2) C - B < = Y ;(3) C - A < = z .
则 C-A 的最大值 即为 1+2 和 3 比较 ,也就是 C-A<=x+y 与 C-A <=z 答案即为 min(x+y,z) (小小取更小),即为从A到C的最短路。
字面理解为B比A最大大x,C比B最大大y,C就比A最大大x+y,C又比A最大大z,所以我们要求一个x+y和z的最小值。
把它扩展为n个点,m条边的图,每一条边都是一个可传递的大小关系。S到T的路径可以看做许多S与T之间的大小关系(T-S < = ... ),我们要求的T-S的最大值就是最小的限制,也就是A到C最短路。
同理 B-A > = x , C-B > = y , C-A > = z ,也可以抽象为 de[t] > = de[f] + d ,这就转变为了最长路问题 ,这是求 C-A 的最小值 , 与上面思想相同。
也就是最大求最短,最小求最长。
关于Dist[]的初始化1.如果将源点到各点的距离初始化为0,最终求出的最短路满足它们之间相互最接近了2.如果将源点到各点的距离初始化为INF(无穷大),其中之1为0,最终求出的最短路满足 它们与该点之间相互差值最大。(from baidubaike)
但是题目里给出的不等式不一定大于小于号的方向相同,如 求最大值时却给出了 D-E > = q , 只需要转化成 E-D < = -q 就可以了。(D到E连了一条边权为-q的边)。
那么问题又来了,不等式一定有解吗??
不一定。
数学上,多个不等式的解集分为 空集 , 有限集,无限集(暂且这么叫qwq)。
发现,若是S无法到T,即为无限多解(没有限制)。若S到T的路径上有环(最短路的负环,最长路的正环),无法取到最大值或最小值。
emmm。。。百度百科上的有关知识
引理:设x=(x1,x2,…,xn)是差分约束系统Ax≤b的一个解,d为任意常数。则x+d=(x1+d,x2+d,…,xn+d)也是该系统Ax≤b的一个解。
定理:将如上差分约束系统
转换成图后,以
为源点得到的最短路径序列为
(如果有解),则
满足
且若
为
任意解,则有
。
栗子 : codevs 2404 糖果
代码 qwq
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #include<cmath> 6 #include<deque> 7 using namespace std; 8 9 int N,K,X,A,B,cnt,f; 10 int first[100010],next[400010],rd[100010]; 11 long long de[100010],ans; 12 bool used[100010]; 13 14 struct maple{ 15 int f,t,d; 16 }Rode[400010]; 17 deque<int> q; 18 19 void Build(int f,int t,int d) 20 { 21 Rode[++cnt]=(maple){f,t,d}; 22 next[cnt]=first[f]; 23 first[f]=cnt; 24 } 25 void SPFA() // 跑最长路 26 { 27 used[0]=1; 28 de[0]=1; // 保证每个人都分到糖果 29 q.push_back(0); 30 while(!q.empty()) 31 { 32 int a=q.front(); 33 q.pop_front(); 34 used[a]=0; 35 for(int i=first[a];i;i=next[i]) 36 if(de[Rode[i].t]<de[a]+Rode[i].d) 37 { 38 de[Rode[i].t]=de[a]+Rode[i].d; 39 if(!used[Rode[i].t]) 40 { 41 used[Rode[i].t]=1; 42 if(!q.empty()&&de[Rode[i].t]>=de[q.front()]) q.push_front(Rode[i].t); 43 else q.push_back(Rode[i].t); 44 ++rd[Rode[i].t]; 45 if(rd[Rode[i].t]>=N) // 判断是否有解 46 { 47 f=1; 48 break; 49 } 50 } 51 } 52 if(f) break; 53 } 54 } 55 int main() 56 { 57 scanf("%d%d",&N,&K); 58 for(int i=1;i<=K;++i) 59 { 60 scanf("%d%d%d",&X,&A,&B); 61 if(X==1) Build(A,B,0),Build(B,A,0); // A = B 62 if(X==2) Build(A,B,1); // B - A > = 1 63 if(X==3) Build(B,A,0); // A - B > = 0 64 if(X==4) Build(B,A,1); // A - B > = 1 65 if(X==5) Build(A,B,0); // B - A > = 0 66 } 67 for(int i=1;i<=N;++i) Build(0,i,0); // i - 0 > = 0 68 SPFA(); 69 if(f) cout<<-1; 70 else{ 71 for(int i=1;i<=N;++i) 72 ans+=de[i]; 73 printf("%lld",ans); 74 } 75 return 0; 76 }
(部分内容参考自各神犇博客,侵删 qwq)


