<学习笔记> tarjan 求强连通分量

时间复杂度 O（n+m）

dfs 求解。

定义 dfn[n]为n当前的时间戳，low[n]为n最早能追溯到的时间戳,可知

 for(int i=first[n];i;i=next[i])
 {
     if(!dfn[Rode[i].t])
     {
          Tarjan(Rode[i].t);
          low[n]=min(low[n],low[Rode[i].t]);
      }
      else
           if(Instack[Rode[i].t])  low[n]=min(low[n],dfn[Rode[i].t]);
    }

 

若回溯时 dfn[n]==low[n]，即找到了一个强连通分量。如图

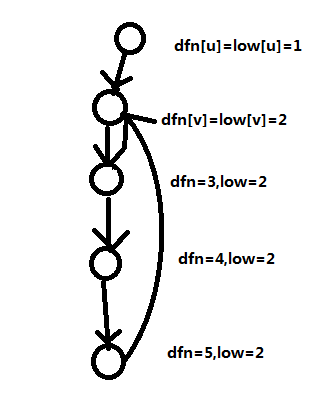
注意一个点也会被看做强连通分量。

若有环套环的情况，tarjan求的是最大的那个。

另外判断Instack是为了避免这样的情况。

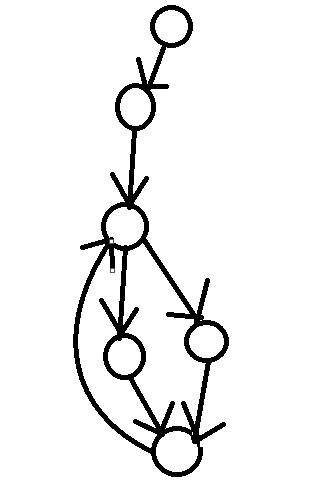
防止不是环中元素的点被计入环。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<vector>
using namespace std;

int N,M,a,b,c,cnt,top,index,scc_cnt;
int first[100010],next[200010];
int dfn[100010],low[100010],Instack[100010],Stack[100010];
int belong_scc[100010];
vector<int> scc[100010];

struct maple{
    int f,t,d;
}Rode[200010];

void Build(int f,int t,int d)
{
    Rode[++cnt]=(maple){f,t,d};
    next[cnt]=first[f];
    first[f]=cnt;
}

void Tarjan(int n)
{
    dfn[n]=low[n]=++index;
    Instack[n]=1;
    Stack[++top]=n;
    for(int i=first[n];i;i=next[i])
    {
        if(!dfn[Rode[i].t]) // 之前没有走过
        {
            Tarjan(Rode[i].t);
            low[n]=min(low[n],low[Rode[i].t]);
        }
        else
              if(Instack[Rode[i].t])  low[n]=min(low[n],dfn[Rode[i].t]);
    }
    if(dfn[n]==low[n]) // 是一个环
    {
        int j;
        ++scc_cnt;
        do{
              j=Stack[top--];
              Instack[j]=0;
              belong_scc[j]=scc_cnt;
              scc[scc_cnt].push_back(j);
        }while(j!=n);
    }
}

int main()
{
    scanf("%d%d",&N,&M);
    for(int i=1;i<=M;++i)
    {
        scanf("%d%d%d",&a,&b,&c);
        Build(a,b,c); 
    }
    Tarjan(1);
    return 0;
}