「算法笔记」线段树优化建图

一、引入

先来看一道题：CF786B Legacy。

题目大意：有 $n$ 个点、$q$ 次操作。每一种操作为以下三种类型中的一种：

• 操作一：连一条 $u\to v$ 的有向边，权值为 $w$。

• 操作二：对于所有 $i\in [l,r]$ 连一条 $u\to i$ 的有向边，权值为 $w$。

• 操作三：对于所有 $i\in [l,r]$ 连一条 $i\to u$ 的有向边，权值为 $w$。

求从点 $s$ 到其他点的最短路。$1\leq n,q\leq 10^5,1\leq w\leq 10^9$。

考虑暴力建图。显然不能通过此题。

这时候就需要用线段树优化建图了。线段树优化建图就是利用线段树，减少连边数量，从而降低复杂度。

二、基本思想

先建一棵线段树。假如现在我们要从 $8$ 号点向区间 $[3,7]$ 的所有点连一条权值为 $w$ 有向边。

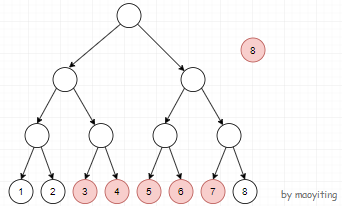
那么怎么连边？把区间 $[3,7]$ 拆成 $[3,4]$、$[5,6]$ 和 $[7,7]$ 然后分别连边。

就这样：（如下图所示。其中黑色普通边的边权为 $0$，粉色边的边权为 $w$。）

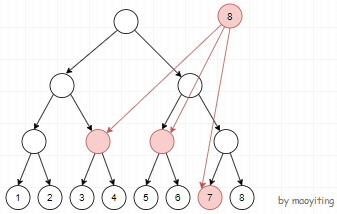
原来我们要连 $5$ 条边，现在只需要连 $3$ 条边，也就是 $\lceil \log_2 7\rceil$ 条边。

于是 $O(n)$ 的边数就优化成了 $O(\log n)$。

那么操作三用和操作二类似的方法连边。从区间 $[3,7]$ 的所有点向 $8$ 号点连一条权值为 $w$ 有向边：（其实就是边反了个方向）

以上是操作二与操作三分开来考虑的情形，那么操作二与操作三相结合该怎么办呢？

考虑建两棵线段树，第一棵只连自上而下的边，第二棵只连自下而上的边。方便起见，我们把第一棵树称作“出树”，第二棵树称作“入树”。

初始时自上而下或自下而上地在每个节点与它的父亲之间连边。由于两棵线段树的叶子节点实际上是同一个点，因此要在它们互相之间连边权为 $0$ 的边。初始时是这样的：

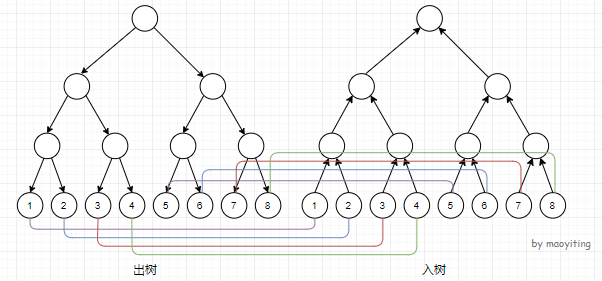
建树部分的代码：（代码中的 $K$ 是一个常数，根据数据范围而定。建出树和入树也可以分别用两个函数实现，这样就用不到 $K$ 了。）

void build(int p,int l,int r){
    if(l==r){a[l]=p;return ;}    //a: 记录叶子节点的编号 
    add(p,p<<1,0),add(p,p<<1|1,0);    //出树（从 p 向 p 的左右儿子连一条边权为 0 的边） 
    add((p<<1)+K,p+K,0),add((p<<1|1)+K,p+K,0);    //入树（从 p 的左右儿子向 p 连一条边权为 0 的边） 
    build(p<<1,l,mid);
    build(p<<1|1,mid+1,r); 
}
//主函数中： 
for(int i=1;i<=n;i++)
    add(a[i],a[i]+K,0),add(a[i]+K,a[i],0);     //两棵线段树的叶子节点之间连边 

接下来：

• 对于操作一，就从入树的叶子节点向出树的叶子节点连边。

• 对于操作二，就从入树的叶子节点向出树中的对应区间连边。

• 对于操作三，就从入树中的对应区间向出树中的叶子节点连边。

举个栗子。比如现在我们要从 $8$ 号点向区间 $[3,7]$ 的所有点连一条权值为 $w$ 有向边。那么就如图所示连边：（为了让图更清楚，图中把入树和出树叶子节点之间相连的边省略了。）

连边部分的代码：

void modify(int p,int l,int r,int lx,int rx,int v,int w){
    if(l>=lx&&r<=rx){    //如果当前区间被涵盖
        if(opt==2) add(v+K,p,w);    //对于操作二，就从入树的叶子节点向出树中的对应区间连边。
        else add(p+K,v,w);    //对于操作三，就从入树中的对应区间向出树中的叶子节点连边。
        return;
    }
    int mid=(l+r)/2;
    if(lx<=mid) modify(p<<1,l,mid,lx,rx,v,w);
    if(rx>mid) modify(p<<1|1,mid+1,r,lx,rx,v,w);
} 
//主函数中：
for(int i=1;i<=m;i++){
    scanf("%lld",&opt);
    if(opt==1) scanf("%lld%lld%lld",&x,&y,&z),add(a[x]+K,a[y],z);    //对于操作一，就从入树的叶子节点向出树的叶子节点连边。
    else{
        scanf("%lld%lld%lld%lld",&x,&l,&r,&w);
        modify(1,1,n,l,r,a[x],w);
    }
}

三、代码实现

CF786B Legacy 无注释完整代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=3e6+5,K=5e5;
int n,m,s,opt,x,y,z,l,r,w,a[N],cnt,hd[N],to[N],nxt[N],val[N],d[N];
bool v[N];
priority_queue<pair<int,int> >q;
void add(int x,int y,int z){
    to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt,val[cnt]=z;
}
void build(int p,int l,int r){
    if(l==r){a[l]=p;return ;}
    int mid=(l+r)/2;
    add(p,p<<1,0),add(p,p<<1|1,0);
    add((p<<1)+K,p+K,0),add((p<<1|1)+K,p+K,0);
    build(p<<1,l,mid);
    build(p<<1|1,mid+1,r); 
}
void modify(int p,int l,int r,int lx,int rx,int v,int w){
    if(l>=lx&&r<=rx){
        if(opt==2) add(v+K,p,w);
        else add(p+K,v,w);
        return;
    }
    int mid=(l+r)/2;
    if(lx<=mid) modify(p<<1,l,mid,lx,rx,v,w);
    if(rx>mid) modify(p<<1|1,mid+1,r,lx,rx,v,w);
} 
void dij(int s){
    memset(d,0x3f,sizeof(d)),d[s]=0;
    q.push(make_pair(0,s));
    while(q.size()){
        int x=q.top().second;q.pop();
        if(v[x]) continue;
        v[x]=1;
        for(int i=hd[x];i;i=nxt[i]){
            int y=to[i],z=val[i];
            if(d[y]>d[x]+z) d[y]=d[x]+z,q.push(make_pair(-d[y],y));
        }
    }
}
signed main(){
    scanf("%lld%lld%lld",&n,&m,&s),build(1,1,n);
    for(int i=1;i<=n;i++)
        add(a[i],a[i]+K,0),add(a[i]+K,a[i],0);
    for(int i=1;i<=m;i++){
        scanf("%lld",&opt);
        if(opt==1) scanf("%lld%lld%lld",&x,&y,&z),add(a[x]+K,a[y],z);
        else{
            scanf("%lld%lld%lld%lld",&x,&l,&r,&w);
            modify(1,1,n,l,r,a[x],w);
        }
    }
    dij(a[s]+K);
    for(int i=1;i<=n;i++)
        printf("%lld%c",d[a[i]]!=0x3f3f3f3f3f3f3f3fll?d[a[i]]:-1,i==n?'\n':' ');
    return 0;
}