「算法笔记」博弈论入门

一、公平组合游戏 ICG

1. 公平组合游戏的定义

若一个游戏满足：

1. 游戏有两个人参与，二者轮流做出决策。
2. 在游戏进程的任意时刻，可以执行的合法行动与轮到哪名玩家无关。
3. 不能行动的玩家判负。

则称该游戏为一个 公平组合游戏。

2. 一些说明

我们把游戏过程中面临的状态称为 局面，整局游戏第一个行动的为 先手，第二个行动的为 后手。我们讨论的博弈问题一般只考虑理想情况，即两人均无失误，都采取 最优策略 行动时游戏的结果。

定义 必胜态 为先手必胜的状态 ，必败态 为先手必败的状态 。注意，在一般确定操作状态的组合游戏中，只会存在这两种状态，如果先手和后手都足够聪明，不会出现介于必胜态和必败态之间的状态。

一个重要的性质：一个状态是必败态当且仅当它的所有后继都是必胜态。一个状态是必胜态当且仅当它至少有一个后继是必败态。特别地，没有后继状态的状态是必败态（因为无法操作则负）。

二、Nim 博弈

\(\text{Nim}\) 游戏是一个公平组合游戏。大概是这样的：

现在有 \(n\) 堆石子，第 \(i\) 堆有 \(a_i\) 个。两人轮流操作，每人每次可以从任选一堆中取走任意多个石子，但是不能不取。取走最后一个石子的人获胜（即无法再取的人就输了）。

结论：\(\text{Nim}\) 博弈先手必胜，当且仅当 \(a_1\oplus a_2\oplus \cdots \oplus a_n\neq 0\)。

证明：为了证明这个结论，我们需要证明：

• 1. 所有石子都被取走是一个必败局面。

• 2. 对于任意一个局面，若 \(a_1\oplus a_2\oplus \cdots \oplus a_n\neq 0\)，一定 能 得到一个 \(a_1\oplus a_2\oplus \cdots \oplus a_n=0\) 的局面。

• 3. 对于任意一个局面，若 \(a_1\oplus a_2\oplus \cdots \oplus a_n=0\)，一定 不能 得到一个 \(a_1\oplus a_2\oplus \cdots \oplus a_n=0\) 的局面。

首先，所有石子都被取走是一个必败局面（对手取走最后一个石子，已经获得胜利），此时显然有  \(a_1\oplus a_2\oplus \cdots \oplus a_n=0\)。

其次，若 \(a_1\oplus a_2\oplus \cdots \oplus a_n=x\neq 0\)，设 \(x\) 的二进制表示下最高位的 \(1\) 在第 \(k\) 位，那么至少存在一堆石子 \(a_i\) 的第 \(k\) 位是 \(1\)。显然 \(a_i\oplus x<a_i\)，于是就可以从第 \(i\) 堆取走若干个石子，使得第 \(i\) 堆的石子数量变为 \(a_i\oplus x\)，就得到了一个 \(a_1\oplus a_2\oplus \cdots \oplus a_n=0\) 的局面。

若 \(a_1\oplus a_2\oplus \cdots \oplus a_n=0\)，假设可以得到一个 \(a_1\oplus a_2\oplus \cdots \oplus a_n=0\) 的局面，其中第 \(i\) 堆的 \(a_i\) 个石子被取成了 \(a_i'\)。由异或的运算可得 \(a_i'=a_i\)，与“不能不取石子”矛盾。所以一定不能得到一个 \(a_1\oplus a_2\oplus \cdots \oplus a_n=0\) 的局面。

综上所述，\(a_1\oplus a_2\oplus \cdots \oplus a_n\neq 0\) 是一个必胜局面，反之必败。

//Luogu P2197
#include<bits/stdc++.h>
#define int long long
using namespace std;
int t,n,x,ans;
signed main(){
    scanf("%lld",&t);
    while(t--){
        scanf("%lld",&n),ans=0;
        for(int i=1;i<=n;i++)
            scanf("%lld",&x),ans^=x;
        puts(ans?"Yes":"No");    //各堆石子数异或起来不等于 0 则必胜，否则必败 
    }
    return 0;
} 

三、有向图游戏

给定一个有向无环图，图中有一个唯一的起点，在起点上放有一枚棋子。两人交替地移动棋子（将棋子从一个点沿有向边移动到另一个点，每次移动一步），无法移动者输。

该游戏被称为 有向图游戏。

事实上，任何一个公平组合游戏都可以转化为有向图游戏。具体方法是，把局面看成图中一个节点，并且从每个局面向沿着合法行动能够到达的下一个局面连有向边。

四、SG 函数

设 \(S\) 表示一个非负整数集合。定义 \(\text{mex}(S)\) 为求出不属于集合 \(S\) 的最小非负整数的运算，即：

\(\text{mex}(S)=\min\limits_{x\in \mathbb{N},x\notin S}\{x\}\)

\(\text{SG}\) 函数的定义如下：最终状态（不可操作状态）的 \(\text{SG}\) 函数为 \(0\)，其余状态的 \(\text{SG}\) 函数为它的后继状态的 \(\text{SG}\) 函数值构成的集合再执行 \(\text{mex}\) 运算的结果。

换一种说法，在有向图游戏中，对于每个节点 \(x\)，设从 \(x\) 出发共有 \(k\) 条有向边，分别到达节点 \(y_1,y_2,\cdots,y_k\)，则：

\(\text{SG}(x)=\text{mex}(\{\text{SG}(y_1),\text{SG}(y_2),\cdots,\text{SG}(y_k)\})\)

举两个栗子，一个状态有 \(2\) 个后继状态，它们的 \(\text{SG}\) 函数分别为 \(2\) 和 \(3\)，则当前状态的 \(\text{SG}\) 函数为 \(0\)；\(2\) 个后继状态的 \(\text{SG}\) 函数分别为 \(0\) 和 \(2\)，则当前状态的 \(\text{SG}\) 函数为 \(1\)。

\(\text{SG}\) 函数判断状态是否必胜的规则是，如果当前状态的 \(\text{SG}\) 函数为 \(0\)，则当前状态必败，否则当前状态必胜。

五、有向图游戏的和

有 \(m\) 个有向图游戏，分别为 \(G_1,G_2,\cdots,G_m\)。定义有向图游戏 \(G\)，它的行动规则是任选某个有向图游戏 \(G_i\)，并在 \(G_i\) 上行动一步。\(G\) 被称为有向图游戏 \(G_1,G_2,\cdots ,G_m\) 的和。

有向图游戏的和的 \(\text{SG}\) 函数值等于它包含的各个子游戏 \(\text{SG}\) 函数值的异或和，即：

\(\text{SG}(G)=\text{SG}(G_1)\oplus \text{SG}(G_2)\oplus \cdots \oplus \text{SG}(G_m)\)

其证明方法与 \(\text{Nim}\) 博弈类似。此处略。

定理：有向图游戏的某个局面必胜，当且仅当该局面对应节点的 \(\text{SG}\) 函数值大于 \(0\)。有向图游戏某个局面必败，当且仅当该局面对应节点的 \(\text{SG}\) 函数值等于 \(0\)。

可以这样理解：

• 在一个没有出边的节点上，棋子不能移动，它的 \(\text{SG}\) 值为 \(0\)，对应必败局面。

• 若一个节点的某个后继节点 \(\text{SG}\) 值为 \(0\)，在 \(\text{mex}\) 运算后，该节点的 \(\text{SG}\) 值大于 \(0\)。这等价于，若一个局面的后继局面中存在必败局面，则当前局面为必胜局面。

• 若一个节点的后继节点 \(\text{SG}\) 值均不为 \(0\)，在 \(\text{mex}\) 运算后，该节点的 \(\text{SG}\) 值为 \(0\)。这等价于，若一个局面的后继局面全部为必胜局面，则当前局面为必败局面。

六、Nim 博弈的变种

1. 阶梯 Nim

顾名思义，就是在阶梯上进行博弈。每层有若干个石子（地面表示第 \(0\) 层），每次可以从任意层的石子中取若干个移动到该层的下一层。

换一种说法：有 \(n\) 堆石子。两人轮流操作，每人每次可以从第 \(i\) 堆的石子中取若干个石子放到第 \(i-1\) 堆里（\(1<i\leq n\)），或者从第 \(1\) 堆的石子中取若干个，无法操作者负。

阶梯 \(\text{Nim}\) 经过转换可以变为 \(\text{Nim}\)。

把石子从奇数堆移动到偶数堆可以理解为拿走石子。那么，如果两人都只移动奇数堆的石子，那么等价于两人在玩 \(\text{Nim}\) 游戏。

考虑有人移动偶数堆的石子到奇数堆怎么处理。先假设 \(\text{Nim}\) 游戏先手必胜，那么先手肯定优先玩 \(\text{Nim}\) 游戏。

若后者试图破坏局面，移动第 \(x\) 堆（\(x\) 为偶数）的若干个石子到 \(x-1\) 堆，那么先手就可以紧接着把他动的那些石子从第 \(x-1\) 堆继续移到第 \(x-2\) 堆上，所以第 \(x-1\) 堆（\(x-1\) 为奇数）的石子数不会有变化，且先后手关系不变，对局面没有影响。

所以阶梯 \(\text{Nim}\) 等价于是奇数堆的 \(\text{Nim}\) 博弈。因此只需考虑奇数堆的石子数异或和是否为 \(0\)（为 \(0\) 则先手必败，否则必胜）。

POJ 1704 Georgia and Bob

题目大意：有 \(n\) 个格子，在某些格子上有一个石子。每个格子最多只能包含一个石子。两人轮流操作，每人每次可以选择一个石子向左移动若干格，但不能越过其他石子或越过左边边缘。不能操作者负。

Solution：

把相邻两个石子之间的距离看作一堆石子中的石子个数，向左移动石子就等价于把第 \(i\) 堆石子移动到第 \(i+1\) 堆里。反一下，就转化为了阶梯 \(\text{Nim}\)。只需考虑奇数堆的石子数异或和是否为 \(0\)（为 \(0\) 则先手必败，否则必胜）。

#include<cstdio>
#include<algorithm>
#define int long long
using namespace std;
const int N=1e3+5;
int t,n,a[N],b[N],ans;
signed main(){
    scanf("%lld",&t);
    while(t--){
        scanf("%lld",&n),ans=0;
        for(int i=1;i<=n;i++)
            scanf("%lld",&a[i]);
        sort(a+1,a+1+n);
        for(int i=1;i<=n;i++)
            b[i]=a[i]-a[i-1]-1;    //把相邻两个石子之间的距离看作一堆石子中的石子个数 
        reverse(b+1,b+1+n);    //反一下转化为阶梯 Nim 
        for(int i=1;i<=n;i+=2) 
            ans^=b[i];    //计算奇数堆石子数的异或和 
        if(ans) puts("Georgia will win");    //先手必胜 
        else puts("Bob will win");    //先手必败 
    }
    return 0;
}

2. 反 Nim 博弈

同样地，反 \(\text{Nim}\) 博弈也是 \(\text{Nim}\) 博弈的一个变种。\(\text{Nim}\) 博弈是取到最后一个石子者胜，那么反 \(\text{Nim}\) 博弈就是取到最后一个石子负。其余条件不变。

即：现在有 \(n\) 堆石子，第 \(i\) 堆有 \(a_i\) 个。两人轮流操作，每人每次可以从任选一堆中取走任意多个石子，但是不能不取。取走最后一个石子的人输。

可以分为两种情况分别讨论：

• \(n\) 堆石子的石子数均为 \(1\)。

• 至少有一堆石子数大于 \(1\)。

对于第一种情况，显然：当 \(n\) 为偶数时，先手必胜，否则必败。

对于第二种情况：

• 当 \(a_1\oplus a_2\oplus \cdots \oplus a_n\neq 0\) 时：

  • 若至少有两堆的石子数大于 \(1\)，此时一定存在一种方式转化为至少有两堆的石子数大于 \(1\) 且各堆石子异或和为 \(0\) 的状态。于是变成了下一种情况（各堆石子异或和为 \(0\) 的情况），相当于是把下一种情况的局面交给后手。此时先手必胜。（见下文）

  • 若只有一堆的石子数大于 \(1\) 时：假设石子数为 \(1\) 的有 \(m\) 堆。若 \(m\) 是奇数，先手就可以将唯一的石子数大于 \(1\) 的那一堆全部取走；反之，就将这堆取到只剩下一个石子。于是就转化为了石子数均为 \(1\) 并且石子堆数为奇数的情况。算上先手的这一次操作，总操作数为偶数。所以先手必胜。

  • 因此，在这种情况下，先手必胜。

• 当 \(a_1\oplus a_2\oplus \cdots \oplus a_n=0\) 时：这样的话至少有两堆的石子数大于 \(1\)。那么先手决策完之后，必定能得到一个 \(a_1\oplus a_2\oplus \cdots \oplus a_n\neq 0\) 的局面，这样便到了先手必胜局（上一个情况）。由于是先手决策完后到了先手必胜局，相当于是把先手必胜局交给了后手。所以当 \(\text{SG}\) 为 \(0\) 时，先手必败。

//LightOJ 1253 Misere Nim
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=110;
int t,n,a[N],k,cnt,ans;
signed main(){
    scanf("%lld",&t);
    while(t--){
        scanf("%lld",&n),ans=cnt=0;
        for(int i=1;i<=n;i++){ 
            scanf("%lld",&a[i]),ans^=a[i];
            if(a[i]>1) cnt++;
        } 
        printf("Case %lld: ",++k);
        if(!cnt) puts(n%2==0?"Alice":"Bob");    //n 堆石子的石子数均为 1 
        else puts(ans?"Alice":"Bob");    //至少有一堆石子数大于 1 
    }
    return 0;
} 

3. Nim-K 游戏

有 \(n\) 堆石子，两人轮流操作，每人每次可以从不超过 \(k\) 堆中取走任意多个石子，但是不能不取。无法再取的人败。

结论：把 \(n\) 堆石子的石子数用二进制表示，统计每一个二进制位上 \(1\) 的个数。若每一位上 \(1\) 的个数对 \(k+1\) 取模全为 \(0\)，则先手必败，否则先手必胜。

\(\text{Nim}\) 游戏可以看做是 \(k=1\) 的 \(\text{Nim}-K\) 游戏，因为异或就相当于把每一位 \(1\) 的个数加起来对 \(2\) 取模。

七、其他

1. 斐波那契博弈

有一堆石子（石子数 \(\geq 2\)），两人轮流操作，先手第一次可以取走任意多个石子（不能不取，也不能全部取完）；接下来每个人取的石子数都不能超过上个人的两倍，但不能不取。无法操作者输。

结论：先手必败，当且仅当石子数为斐波那契数。

2. 无向图删边游戏

无向图删边游戏

八、SG 函数博弈

1. 小练习

Exercise 1

题目大意：有一堆石子，共有 \(n\) 个。两人轮流操作，每人每次可以从这堆石子里面取 \(l\sim r\) 个石子，不能操作者负。

Solution：打表找规律。打表代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
int n,l,r,sg[N];
bool vis[N];
signed main(){
    scanf("%lld%lld%lld",&n,&l,&r);
    for(int i=1;i<=n;i++){
        memset(vis,0,sizeof(vis));
        for(int j=l;j<=r;j++)    //每次可以取 l~r 个 
            if(i>j) vis[sg[i-j]]=1;    //标记后继状态
        for(int j=0;j<=n;j++)
            if(!vis[j]){sg[i]=j;break;}     //mex 运算 
    }
    for(int i=1;i<=n;i++)
        printf("%lld%c",sg[i],i==n?'\n':' ');
    return 0;
} 
/*
Input: 30 3 7
Output: 0 0 0 1 1 1 2 2 2 3 0 0 0 1 1 1 2 2 2 3 0 0 0 1 1 1 2 2 2 3
*/

容易发现 \(\text{SG}(i)=\lfloor \frac{i\bmod (l+r)}{l}\rfloor\)。

Exercise 2

题目大意：现在有 \(n\) 堆石子，第 \(i\) 堆有 \(a_i\) 个，两人轮流操作，每人每次可以从一堆石子中取任意多个，也可以把一堆石子分成两堆。不能操作者负。

Solution：

一堆石子变成两堆，相当于是变成了两个独立的游戏。那么这个游戏的 \(\text{SG}\) 值就是其子游戏的异或值。

所以 \(\text{SG}(i)=\text{mex}(\text{SG}(i-j),\text{SG}(i-j)\oplus \text{SG}(j))\)。

\(\text{SG}(i-j)\) 是从石子中选 \(j\) 个，\(\text{SG}(i-j)\oplus \text{SG}(j)\) 是将石子分为两堆，分别有 \(i-j\) 个和 \(j\) 个石子。

然后呢？打表找规律！

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
int n,sg[N];
bool vis[N];
signed main(){
    scanf("%lld",&n);
    for(int i=1;i<=n;i++){
        memset(vis,0,sizeof(vis));
        for(int j=1;j<=i;j++) 
            vis[sg[i-j]]=1;
        for(int j=1;j<i;j++)
            vis[sg[j]^sg[i-j]]=1;    //sg[j] 和 sg[i-j] 肯定已经算出来了 
        for(int j=0;j<=n;j++)
            if(!vis[j]){sg[i]=j;break;} 
    }
    for(int i=1;i<=n;i++)
        printf("%lld%c",sg[i],i==n?'\n':' ');
    return 0;
} 
/*
Input: 30
Output: 1 2 4 3 5 6 8 7 9 10 12 11 13 14 16 15 17 18 20 19 21 22 24 23 25 26 28 27 29 30
*/

容易发现，mod 4 一个周期。

Exercise 3

题目大意：有一堆石子，共有 \(n\) 个。两人轮流操作，每人每次可以从取当前个数的因数个石子（不能是本身），不能操作者（剩下一个）负。

Solution：

\(\text{SG}(i)=\text{mex}(\text{SG}(i-j))\)，其中 \(j\mid i\)。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
int n,sg[N];
bool vis[N];
signed main(){
    scanf("%lld",&n);
    for(int i=1;i<=n;i++){
        memset(vis,0,sizeof(vis));
        for(int j=1;j<i;j++) 
            if(i%j==0) vis[sg[i-j]]=1;
        for(int j=0;j<=n;j++)
            if(!vis[j]){sg[i]=j;break;} 
    }
    for(int i=1;i<=n;i++)
        printf("%lld%c",sg[i],i==n?'\n':' ');
    return 0;
} 
/*
Input: 20
Output: 0 1 0 2 0 1 0 3 0 1 0 2 0 1 0 4 0 1 0 2
*/

发现 \(\text{SG}(i)\) 是 \(i\) 在二进制下末尾 \(0\) 的个数。

Exercise 4

题目大意：有一堆石子，共有 \(n\) 个。两人轮流操作，每人每次可以取与当前个数互质的数字个石子，不能操作者负。

Solution：

\(\text{SG}(i)=\text{mex}(\text{SG}(i-j))\)，其中 \(\text{gcd}(i,j)=1\)。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
int n,sg[N];
bool vis[N];
int gcd(int x,int y){
    if(!y) return x;
    return gcd(y,x%y);
}
signed main(){
    scanf("%lld",&n);
    for(int i=1;i<=n;i++){
        memset(vis,0,sizeof(vis));
        for(int j=1;j<=i;j++) 
            if(gcd(i,j)==1) vis[sg[i-j]]=1;
        for(int j=0;j<=n;j++)
            if(!vis[j]){sg[i]=j;break;} 
    }
    for(int i=1;i<=n;i++)
        printf("%lld%c",sg[i],i==n?'\n':' ');
    return 0;
} 
/*
Input: 30
Output: 1 0 2 0 3 0 4 0 2 0 5 0 6 0 2 0 7 0 8 0 2 0 9 0 3 0 2 0 10 0
*/

发现偶数的 \(\text{SG}\) 值为 \(0\)，奇数的 \(\text{SG}\) 值为它的最小质因子在质数表中的编号。特别地，\(\text{SG}(1)=1\)。

Exercise 5

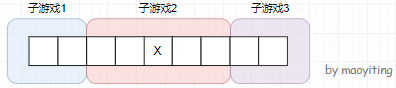
题目大意：有⼀张 \(1\times n\) 的纸条，两人轮流在格子里画 \(\text{X}\) ，画了连续的三个 \(\text{X}\) 者获胜。

Solution：

放了一个后，左右各延伸的两格都不能放，那么左右两边的纸条就是独立的游戏，于是 \(\text{SG}\) 值异或一下就行了（中间的是一个必胜局面，也要作为一个游戏，也就是说一共有 \(3\) 个子游戏）。

2. LOJ 10243 移棋子游戏

题目大意：给定一个 \(n\) 个节点的有向无环图，图中某些节点上有棋子。两人交替地移动棋子（将棋子从一个点沿有向边移动到另一个点，每次移动一步），无法移动者负。问先手是否必胜。

Solution：

\(\text{DFS}\) 出每个节点的 \(\text{SG}\) 值，最后整个游戏的 \(\text{SG}\) 函数值就是每一个棋子的 \(\text{SG}\) 值的异或和。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e3+5,M=6e3+5;
int n,m,k,x,y,cnt,hd[N],to[M],nxt[M],sg[N],ans;
bool v[N];
void add(int x,int y){
    to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt;
}
int solve(int x){
    if(v[x]) return sg[x];
    bool vis[N];
    v[x]=1,memset(vis,0,sizeof(vis));
    for(int i=hd[x];i;i=nxt[i]){
        int y=to[i];
        vis[solve(y)]=1;
    }
    for(int i=0;i<=n;i++)
        if(!vis[i]) return sg[x]=i;    //mex 运算 
}
signed main(){
    scanf("%lld%lld%lld",&n,&m,&k);
    for(int i=1;i<=m;i++)
        scanf("%lld%lld",&x,&y),add(x,y);
    for(int i=1;i<=n;i++) sg[i]=solve(i);    //计算每个节点的 SG 值 
    for(int i=1;i<=k;i++)
        scanf("%lld",&x),ans^=sg[x];    //最后整个游戏的 SG 函数值就是每一个棋子的 SG 值的异或和
    puts(ans?"win":"lose");
    return 0;
}

3. PE306 Paper-strip Game

题目大意：\(n\) 个白色方块，两人轮流操作，每人每次可以选择两个连续的白色方块并将其涂成黑色。不能操作者负。问对于所有的 \(n\) 满足 \(1\leq n\leq 10^6\)，有多少个值可以使得先手必胜。

Solution：

选择两个连续的白色方块并将其涂成黑色相当于把 \(i\) 个白色方块分为了两部分（不算中间 \(2\) 个黑色方块的部分），分别有 \(j\) 个和 \(i-j-2\) 个白色方块。相当于是变成了两个独立的游戏。

所以 \(\text{SG}(i)=\text{mex}(\text{SG}(j)\oplus \text{SG}(i-j-2))\)。特别地，\(\text{SG}(1)=0,\text{SG}(2)=1\)。

然后就可以打表找规律了。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
int n,sg[N];
bool vis[N];
signed main(){
    scanf("%lld",&n),sg[1]=0,sg[2]=1;
    for(int i=3;i<=n;i++){
        memset(vis,0,sizeof(vis));
        for(int j=1;j<=i-2;j++)
            vis[sg[j]^sg[i-j-2]]=1;
        for(int j=0;j<=n;j++)
            if(!vis[j]){sg[i]=j;break;} 
    }
    for(int i=1;i<=n;i++)
        printf("%lld%c",sg[i],i==n?'\n':' ');
    return 0;
} 
//Input: 1000 

拖动窗口找循环节。前两行会有问题，后面的就是循环节。循环节有 \(34\) 位。放个图（每行有 \(34\) 个数）：

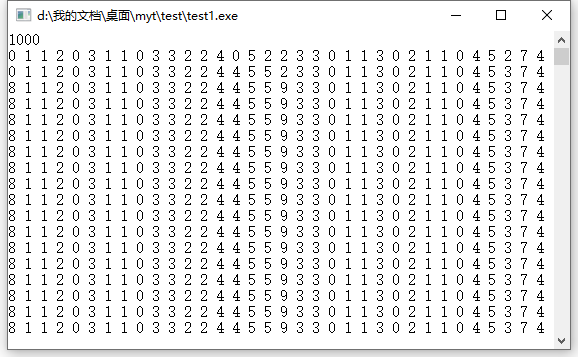
前两行共 \(34\times 2=68\) 个数中，\(\text{SG}\) 值大于 \(0\) 的共有 \(55\) 个。后面的每一行，即每 \(34\) 个数中，\(\text{SG}\) 值大于 \(0\) 的共有 \(29\) 个。\((1000000-68)\bmod 34=26\)，循环节的前 \(26\) 个数中，\(\text{SG}\) 值大于 \(0\) 的共有 \(22\) 个，所以答案为 \(55+\lfloor\frac{1000000-68}{34}\rfloor \times 29+22=852938\)。

4. POJ2311 Cutting Game

题目大意：给定 \(n\times m\) 的矩阵网格纸。两人轮流操作，每人每次可以任选一张矩阵网格纸（游戏开始时，只有一张 \(n\times m\) 的矩阵网格纸，在游戏的过程中，可能会有若干张大小不同的矩形网格纸），沿着某一行或者某一列的格线，把它剪成两部分。首先剪出 \(1\times 1\) 的玩家获胜。问先手是否必胜。

Solution：

在此题中，不能行动的局面，即 \(1\times 1\) 的纸张，是一个必胜局面。而 \(\text{ICG}\) 是以必败局面收尾的。因此，我们需要作出一些转化。

思考哪些局面是必败局面。

首先，对于任何一人，都不会剪出 \(1\times x\) 或 \(x\times 1\) 的纸张，否则必败（因为对手就可以剪出 \(1\times 1\) 从而获胜）。其次，能够剪出 \(1\times 1\) 的方法必定要经过 \(2\times 2\)，\(2\times 3\) 和 \(3\times 2\) 三种局面之一。而在这三种局面下，先手无论如何行动，都会剪出 \(1\times x\) 或 \(x\times 1\) 的形状。所以 \(2\times 2\)，\(2\times 3\) 和 \(3\times 2\) 是必败局面。那么我们就可以把这三者作为终止局面判负。

把这张纸剪成了两部分，相当于是变成了两个独立的游戏。与之前一样类似计算即可。

\(\text{SG}(n,m)=\text{mex}(\text{SG}(i,m) \oplus \text{SG}(n-i,m),\text{SG}(n,i)\oplus \text{SG}(n,m-i))\)

其中 \(\text{SG}(i,m) \oplus \text{SG}(n-i,m)\) 为沿着第 \(i\) 行下边的格线剪开，\(\text{SG}(n,i)\oplus \text{SG}(n,m-i)\) 为沿着第 \(i\) 列右边的格线剪开。

#include<cstdio>
#include<cstring>
#define int long long
using namespace std;
const int N=210;
int n,m,sg[N][N];
bool v[N][N],vis[N];
int solve(int x,int y){
    if(v[x][y]) return sg[x][y];
    bool vis[N];
    v[x][y]=1,memset(vis,0,sizeof(vis));
    for(int i=2;i<=x-i;i++)
        vis[solve(i,y)^solve(x-i,y)]=1;
    for(int i=2;i<=y-i;i++)
        vis[solve(x,i)^solve(x,y-i)]=1;
    for(int i=0;i<=200;i++)
        if(!vis[i]) return sg[x][y]=i;
}
signed main(){
    sg[2][2]=sg[2][3]=sg[3][2]=0,v[2][2]=v[2][3]=v[3][2]=1;    //2*2,2*3,3*2 的局面已确定为是必败局面 
    while(~scanf("%lld%lld",&n,&m)) puts(solve(n,m)?"WIN":"LOSE");
    return 0;
}

5. Luogu P1290 欧几里德的游戏

题目大意：给定两个正整数 \(m\) 和 \(n\)，两人轮流操作，每人每次可以选择其中较大的数，减去较小数的正整数倍，要求得到的数不能小于 \(0\)。得到了 \(0\) 者胜。

Solution：

暴力 \(\text{SG}\)：\(\text{SG}(m,n)=\text{mex}(\text{SG}(m,n-m),\text{SG}(m,n-2m),\cdots,\text{SG}(m,n\bmod m))\)。特别地，\(\text{SG}(m,0)=0\)

想办法简化计算过程。我们发现：

• \(\text{SG}(m,n)=\text{mex}(\text{SG}(m,n-m),\text{SG}(m,n-2m),\cdots,\text{SG}(m,n\bmod m))\)

• \(\text{SG}(m,n-m)=\text{mex}(\text{SG}(m,n-2m),\cdots,\text{SG}(m,n\bmod m))\)

因此，\(\text{SG}(m,n)\) 可以由 \(\text{SG}(m,n-m)\) 推导。容易得出，\(\text{SG}(m,n\bmod m+m)=\text{mex}(\text{SG}(m,n\bmod m))\)。

• 当 \(\text{SG}(m,n\bmod m)=0\)，则 \(\text{SG}(m,n\bmod m+m)=1,\text{SG}(m,n\bmod m+2m)=2,\text{SG}(m,n\bmod m+3m)=3\cdots\) 依次类推，直到 \(\text{SG}(m,n)\)。此时为必胜局。

• 当 \(\text{SG}(m,n\bmod m)\neq 0\)，则 \(\text{SG}(m,n\bmod m+m)=0,\text{SG}(m,n\bmod m+2m)=1,\text{SG}(m,n\bmod m+3m)=2\cdots\) 依次类推，直到 \(\text{SG}(m,n)\)。此时视 \(n-m=n\bmod m\) 的情况而定。

因此，只需计算 \(\text{SG}(m,n\bmod m)\) 再加以讨论即可。

#include<bits/stdc++.h>
#define int long long
using namespace std;
int t,n,m;
bool solve(int m,int n){    //m<n
    if(!m) return 0;
    if(solve(n%m,m)==0) return 1;    //当 SG(m,n%m)=0 时，为必胜局面。由于 n%m<m，所以这里写成 SG(n%m,m)。 
    return n-m==n%m?0:1;    //当 SG(m,n%m)!=0 时，若 n=n%m+m，也就是 n-m=n%m 时，SG 值为 0；否则大于 0。 
}
signed main(){
    scanf("%lld",&t);
    while(t--){
        scanf("%lld%lld",&m,&n);
        if(m>n) swap(n,m);
        puts(solve(m,n)?"Stan wins":"Ollie wins");
    }
    return 0;
}

6. Luogu P2148「SDOI 2009」E&D

题目大意：有 \(2n\) 堆石子，编号为 \(1\sim 2n\)。将第 \(2k-1\) 堆与第 \(2k\) 堆 （\(1\leq k\leq n\)）视为同一组。 一次分割操作指的是，任取一堆石子，将其移走，然后分割它同一组的另一堆石子，从中取出若干个石子放在被移走的位置，组成新的一堆。操作完成后，所有堆的石子数必须保证大于 \(0\)。两人轮流进行分割操作，无法操作者负。

Solution：

一组数看作一个 \(\text{ICG}\)。对于单个游戏 \((a,b)\)，可以转移到 \((c,d)\)，满足 \(c+d=a\) 或 \(c+d=b\)。

我们只关心每一个 \(\text{ICG}\) 中的 \(\text{mex}(\{\text{SG}(c,d)\mid c+d=a\},\{\text{SG}(c,d)\mid c+d=b\})\)。因此对于每一个 \(a\)，考虑所有 \(c+d=a\) 的 \((c,d)\) 的 \(\text{SG}\) 值的取值集合。

打个表：（用二进制表示。可以用 \(\text{bitset}\) 存）

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=10,M=15;
int n;
bitset<N>s[M];
int mex(bitset<N>b){    //mex 操作 
    int cnt=0;
    while(b[cnt]) cnt++;
    return cnt;
} 
signed main(){
    scanf("%lld",&n);
    for(int i=2;i<=n;i++)    //a
        for(int j=1;j<=n&&i-j>=1;j++)    //c=i,d=i-j 
            s[i].set(mex(s[j]|s[i-j])); 
    for(int i=1;i<=n;i++)
        printf("%lld: ",i),cout<<s[i],printf("%c",i%5?' ':'\n');
    return 0; 
}
/*
Input: 10
Output:
1: 0000000000 2: 0000000001 3: 0000000010 4: 0000000011 5: 0000000100
6: 0000000101 7: 0000000110 8: 0000000111 9: 0000001000 10: 0000001001
*/ 

发现，关于 \(a\) 的 \(\text{SG}\) 集合即为 \(a-1\) 的二进制表示中，值为 \(1\) 的位（\(s_i\) 等于 \(i-1\) 的二进制表示）。

比如 \(\{\text{SG}(c,d)\mid c+d=6\}=\{0,2\}\)，则 \(\text{mex}(\{\text{SG}(c,d)\mid c+d=6\})=1\)（即二进制下最低位的 \(0\) 的位置）。

然后回到一个 \(\text{ICG}\) 游戏 \((a,b)\) 的初始局面。

\(\{\text{SG}(c,d)\mid c+d=a\}=(a-1)_2,\{\text{SG}(c,d)\mid c+d=b\}=(b-1)_2\)

\(\text{SG}(a,b)=\text{mex}(\{\text{SG}(c,d)\mid c+d=a\},\{\text{SG}(c,d)\mid c+d=b\})\)
\(=\text{mex}(\{(a-1)_2\},\{(b-1)_2\})=\text{mex}(\{((a-1)\ \text{or} \ (b-1))_2\})\)

利用上述结论，我们取 \((a-1)\ \text{or} \ (b-1)\) 在二进制表示下最低位的 \(0\) 的位置即为 \(\text{SG}(a,b)\)。

最后异或一下就行了。

#include<bits/stdc++.h>
#define int long long
using namespace std;
int t,n,ans,a,b;
int mex(int x){    //求 x 二进制表示下最低位的 0 的位置 
    int cnt=0;
    while(x&1) x>>=1,cnt++;
    return cnt; 
}
signed main(){
    scanf("%lld",&t);
    while(t--){
        scanf("%lld",&n),ans=0;
        for(int i=1;i<=n;i+=2){
            scanf("%lld%lld",&a,&b);
            ans^=mex((a-1)|(b-1));    //SG(a,b)=mex((a-1)|(b-1))
        }
        puts(ans?"YES":"NO");
    }
    return 0;
}

九、博弈 DP 

1. AGC002E Candy Piles

题目大意：有 \(n\) 堆糖果，第 \(i\) 堆有 \(a_i\) 个。两人轮流操作，每人每次可以进行一下两个操作中的一个：

• 1. 选择剩余糖果数量最多的一堆，然后吃掉该堆中的所有糖果。

• 2. 从剩下的还有一个或多个糖果的每个堆中，吃一个糖果。

吃完最后一个糖果者负。问先手必胜还是后手必胜。\(1\leq n\leq 10^5,1\leq a_i\leq 10^9\)。

Solution：

放在二维方格上表示。如图所示，按 \(a_i\) 从大到小排序，那么对于吃掉糖果数量最多的一堆，实际上就是消去最左边一行；对于取走每堆吃一个，实际上就是消去最下面一行。 可以看作，初始在位置 \((1,1)\)，每次往右走或往上走一步。当走到边界时，所有糖果刚好被吃完。

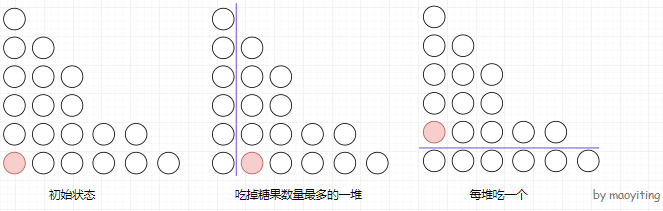
考虑 \(\text{DP}\)。令 \(f_{i,j}\) 表示走到 \((i,j)\) 的胜负情况。

首先，若 \((i,j)\) 为边界，那它一定是必败态。其次，若 \((i,j)\) 的上面和右边都是必败态，那么当前的 \((i,j)\) 对于当前的执行者就是必败态；反之，当任意一个不是必败态时，对于当前的执行者就是必胜态。最后状态取反。

\(f_{i,j}=\neg(f_{i+1,j}\vee f_{i,j+1})\)。其中，\(\neg\) 是逻辑非，\(\vee\) 是逻辑或。

由于是从 \((1,1)\) 出发，我们要知道 \((1,1)\) 的胜负情况。若 \((1,1)\) 为必败态，则先手必胜，否则后手必胜。

显然直接这样做是不能通过这道题的。考虑打表找规律。打表代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e3+5;
int n,a[N],f[N][N],vis[N][N],ans[N][N],mx;
bool cmp(int x,int y){
    return x>y; 
}
int dfs(int x,int y){
    if(~f[x][y]) return f[x][y];
    if(!vis[x+1][y]||!vis[x][y+1]||!vis[x+1][y+1]) return 0;    //边界情况 
    return f[x][y]=!(dfs(x+1,y)|dfs(x,y+1));    //转移 
}
signed main(){
    scanf("%lld",&n);
    for(int i=1;i<=n;i++)
        scanf("%lld",&a[i]),mx=max(mx,a[i]);
    sort(a+1,a+1+n,cmp);    //从大到小排序 
    memset(f,-1,sizeof(f));
    for(int i=1;i<=n;i++)
        for(int j=1;j<=a[i];j++) vis[j][i]=1;    //构造网格图，标记位置 
    for(int i=mx;i>=1;i--,puts(""))    //行 
        for(int j=1;j<=n;j++)    //列 
            if(vis[i][j]) printf("%lld",dfs(i,j));    //输出走到 (i,j) 的胜负情况 
    return 0;
}
/*
Input:
10
8 8 8 8 7 5 5 5 3 3
*/

容易发现，除了边界外，同一对角线上的点胜负情况相同。

所以 \((1,1)\) 的胜负状态等同于 \((i,i)\)。那么，若我们知道了 \((i,i)\) 的胜负情况，就知道了 \((1,1)\) 的胜负情况。

于是我们可以通过求 \(i\) 最大的 \((i,i)\) 的胜负状态，来求出 \((1,1)\) 的胜负状态。

观察一下打表代码的输出，可以发现，只要判一下 \(i\) 最大的 \((i,i)\) 向上/向右到边界的距离的奇偶性就可以知道 \((i,i)\) 的胜负状态。若其中一个方向的距离为奇数，则 \((i,i)\) 为必败态，否则为必胜态。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
int n,a[N],k1,k2;
bool cmp(int x,int y){
    return x>y;
}
signed main(){
    scanf("%lld",&n);
    for(int i=1;i<=n;i++)
        scanf("%lld",&a[i]);
    sort(a+1,a+1+n,cmp);
    for(int i=1;i<=n;i++)
        if(i+1>a[i+1]){    //找到 i 最大的 (i,i)
            k1=a[i]-i,k2=0;
            for(int j=i+1;j<=n;j++)
                if(a[j]==i) k2++;
            break;
        }
    if(k1&1||k2&1) puts("First");
    else puts("Second");
    return 0;
}

十、习题

• SPOJ 11414 COT3 - Combat on a tree
• Luogu P1199 三国游戏