「笔记」组合入门题选做

相关内容：组合入门与应用。（数学公式加载好慢/kk）

一、组合基础题

1. [HNOI2008] 越狱

题目大意：监狱有 \(n\) 个房间，每个房间关押一个犯人，有 \(m\) 种宗教，每个犯人会信仰其中一种。如果相邻房间的犯人的宗教相同，就可能发生越狱，求有多少种状态可能发生越狱。\(m\leq 10^8,n\leq 10^{12}\)。

Solution：

考虑取补集。

因为共有 \(n\) 个房间，每个房间有 \(m\) 个选择。则总方案数为 \(m^n\) 。

相邻房间的犯人的宗教都不相同，就不会发生越狱。第一个房间有 \(m\) 个选择，后面的每一个都要和前一个不同，所以后面的每个房间都有 \(m-1\) 个选择。则不会越狱的方案数为 \(m(m-1)^{n-1}\)。

那么，会发生越狱的方案数为  \(m^n-m(m-1)^{n-1}\) 。

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int mod=1e5+3;
int n,m,ans;
int mul(int x,int n,int mod){
    int ans=mod!=1;
    for(x%=mod;n;n>>=1,x=x*x%mod)
        if(n&1) ans=ans*x%mod;
    return ans;
}
signed main(){
    scanf("%lld%lld",&m,&n);
    printf("%lld\n",(mul(m,n,mod)-m*mul(m-1,n-1,mod)%mod+mod)%mod);
    return 0;
}

补充：若改为 \(|n|\leq 10^5\)（指 \(n\) 的长度不超过 \(10^5\)），答案对一个质数取模，怎么做呢？

欧拉定理：若 \(\gcd(a,m)=1\)，则 \(a^{\varphi(m)}\equiv 1 \pmod m\)。

费马小定理：若 \(m\) 为质数，且 \(\gcd(a,m)=1\)，则 \(a^{m-1}\equiv 1 \pmod m\)。

\(m^n=m^{k\cdot (p-1)+r}=(m^{p-1})^k\cdot m^r\)

根据费马小定理得，\(m^{p-1}\equiv 1 \pmod p\)，那么 \((m^{p-1})^k\equiv 1 \pmod p\)。

所以计算 \(m^r\) 就可以了。

例子：计算 \(2^{100}\) 除以 \(13\) 的余数。

\(2^{100} \bmod 13=2^{12\times 8+4} \bmod 13=(2^{12})^8\cdot 2^4 \bmod 13=2^4 \bmod 13=3\)

回到题目。我们先将大整数 \(n\) 对 \(p-1\) 取模，然后对取模后的整数进行快速幂。（还是用之前那个式子）

2. [Usaco2008 Oct] 建造栅栏

题目大意：一根长度为 \(n\) 的木板，你需要将其切成四条边，使得边的长度为整数且这四条边可以构成一个面积非零的四边形。求方案数。\(n\leq 2500\)。

Solution：

构成四边形的条件是：任意三边之和大于第四边。也就是任意 \(a+b+c>d\)，可以得到 \(d<\frac{n}{2}\)。（不存在 \(\geq \frac{n}{2}\) 的边）

考虑取补集。

• 总方案数：长度为 \(n\) 的木板，有 \(n-1\) 个切点，那么 \(n-1\) 个切点切三刀的方案数就是 \(C_{n-1}^3\)。（插板法）

• 存在 \(\geq \frac{n}{2}\) 的边的方案数（即不能构成四边形的方案数）：枚举最长边 \(i\)，则剩下三边之和为 \(n-i\)。类似地，长度为 \(n-i\) 的木板，有 \(n-i-1\) 个切点，那么 \(n-i-1\) 个切点切两刀的方案数就是 \(C_{n-i-1}^2\)。则存在 \(\geq \frac{n}{2}\) 的边的方案数为：\(4\times \sum_{i=\lceil \frac{n}{2}\rceil}^{n-3} C_{n-i-1}^2\)。其中乘 \(4\) 是因为四条边都有可能是最长边。

答案为 \(C_{n-1}^3-4\times \sum\limits_{i=\lceil \frac{n}{2}\rceil}^{n-3} C_{n-i-1}^2\)。时间复杂度： \(O(n)\)。

#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,ans,sum;
signed main(){
    scanf("%lld",&n);
    ans=(n-1)*(n-2)*(n-3)/6;    //C(n-1,3)=(n-1)*(n-2)*(n-3)/(3*2*1)=(n-1)*(n-2)*(n-3)/6
    for(int i=ceil(n/2.0);i<=n-3;i++)
         sum=sum+4*((n-i-1)*(n-i-2)/2);    //4*C(n-i-1,2)
    printf("%lld\n",ans-sum);
    return 0;
}

3. BZOJ 3907 网格

题目大意：给出一个左下角为 \((0,0)\) 右上角为 \((n,m)\) 的网格图。现在你想要从左下角走到右上角，期间只能向上、右两个方向走，且经过的所有格子 \((x,y)\) 需满足 \(x\geq y\)。求方案数。

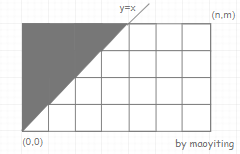
Solution：

向上或向右走，从 \((0,0)\) 走到 \((n,m)\)一共要走 \(n+m\) 步（向右走 \(n\) 步，向上走 \(m\) 步）。不妨把向上定义为 \(1\)，向右定义为 \(0\)。那么一共要有 \(n\) 个 \(0\)，\(m\) 个 \(1\)。经过的所有格子 \((x,y)\) 需满足 \(x≥y\)，也就是当前走的向右的步数要大于等于向上的步数，即前缀中 \(0\) 的个数要大于等于前缀 \(1\) 的个数。

问题转化为，求有多少个有 \(n\) 个 \(0\)，\(m\) 个 \(1\)，并且任意前缀中 \(0\) 的个数都大于等于前缀 \(1\) 的个数的序列。用之前卡特兰数部分证明 \({Cat}_n=\frac{1}{n+1}\times C_{2n}^n\) 的方法，可以得到答案为，\(C_{n+m}^n-C_{n+m}^{m-1}\)。

高精度。我选择 Python 2.7 2333。

f={}
def C(n,m):
    return f[n]/f[m]/f[n-m];
n,m=raw_input().split()
n=int(n)
m=int(m)
f[0]=1
for i in range(1,1+n+m):    # range(1,n+m) 不包括 n+m，所以要 range(1,1+n+m)
    f[i]=f[i-1]*i
print (C(n+m,m)-C(n+m,m-1))

关于 \(\text{Catalan}\) 数的一些补充：以下问题都与 \(\text{Catalan}\) 数有关：

1. \(n\) 个左括号和 \(n\) 个右括号组成的合法括号序列的数量为 \(Cat_n\)。
2. \(1,2,...,n\) 经过一个栈，形成的合法出栈序列的数量为 \(Cat_n\)。（若用 \(0\) 表示入栈，\(1\) 表示出栈，那么可以得到一个 \(01\) 序列，并且前缀 \(0\) 的个数都不少于 \(1\) 的个数）
3. \(n\) 个节点构成的不同二叉树的数量为 \(Cat_n\)。
4. 在平面直角坐标系上，每一步只能向上或向右走，从 \((0,0)\) 走到 \((n,n)\) 并且除两个端点外不接触直线 \(y=x\) 的路线数量为 \(2Cat_{n-1}\)。

4. [SDOI2016] 排列计数

题目大意：求有多少种长度为 \(n\) 的序列 \(A\)，满足以下条件：

• \(1\) 到 \(n\) 这 \(n\) 个数在序列中各出现了一次。

• 若第 \(i\) 个数 \(A_i\) 的值为 \(i\)，则称 \(i\) 是稳定的。序列恰好有 \(m\) 个数是稳定的。

\(T\leq 5\times 10^5,n\leq 10^6,m\leq 10^6\)，对 \(10^9+7\) 取模。

Solution：

\(n\) 个数中选 \(m\) 个数是稳定的，方案数为 \(C_n^m\)。

因为题目要求序列恰好 \(m\) 个数是稳定的，则剩下的 \(n-m\) 个数必须不稳定。即剩下的 \(n-m\) 个数必须满足 \(A_i\neq i\)。其实就是错排问题。

所以答案为 \(C_n^m\times D_{n-m}\)。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+5,mod=1e9+7;
int t,n,m,f[N],g[N],d[N];
int mul(int x,int n,int mod){
    int ans=mod!=1;
    for(x%=mod;n;n>>=1,x=x*x%mod)
        if(n&1) ans=ans*x%mod;
    return ans;
}
void init(){ 
    int n=1e6;
    f[0]=g[0]=1;
    for(int i=1;i<=n;i++)
        f[i]=f[i-1]*i%mod;
    g[n]=mul(f[n],mod-2,mod);
    for(int i=n-1;i;i--)
        g[i]=g[i+1]*(i+1)%mod;
} 
int solve(int n,int m){
    return f[n]*g[m]%mod*g[n-m]%mod;
} 
signed main(){
    scanf("%lld",&t),init();
    d[0]=1,d[1]=0,d[2]=1;
    for(int i=3;i<=1e6;i++)
        d[i]=(i-1)*(d[i-1]+d[i-2])%mod;     //错排 
    while(t--){
        scanf("%lld%lld",&n,&m);
        printf("%lld\n",solve(n,m)*d[n-m]%mod);
    }
    return 0;
}

5. CF886E Maximum Element

题目大意：有人写了一个序列求 \(\max\)，它长下面这样：

int fast_max(int n,int a[]) { 
    int ans=0;
    int offset=0;
    for(int i=0;i<n;++i)
        if(ans<a[i]) ans=a[i],offset=0;
        else{
            offset=offset+1;
            if(offset==k) return ans; 
        }
    return ans;
}//这个函数的原理是：如果碰到一个数后面连续的k个数都比它小，那么就把这个数当做序列的最大值。

 求有多少个 \(1\) 到 \(n\) 的排列在这个函数的计算下答案不为 \(n\)（即返回错误的结果）。\(n,k\leq 10^6\)。

Solution：

考虑暴算，发现基本上枚举个什么东西可行的情况都包含一个前提：在此之前函数并没有退出。

那我们不妨来 dp 这个东西。

在只对元素大小关系敏感的题里头可以将一段数等价地看作是相对大小不变的排列，合并的时候注意乘上相应的组合数即可。

令 \(f_i\) 表示 \(1\) 到 \(i\) 的排列当中有多少个是运行完整个循环之后还没有退出的。

怎么算呢?

最大值 \(i\) 必然出现，并且只可能位于 \([i-k+1,i]\)。

考虑枚举最大值出现的位置 \(j\)。

除去最大值 \(i\)，还有 \(i-1\) 个数。选出 \(i-j\) 个数放在 \(j\) 后面，这 \(i-j\) 个数共有 \((i-j)!\) 种排列，所以放在后面有 \(C_{i-1}^{i-j}\times (i-j)!\) 种方案。前面的 \(j-1\) 个数共有 \(f_{j-1}\) 种。所以可以得到：\(f_i=\sum_{j=i-k+1}^i f_{j-1}\times C_{i-1}^{i-j}\times (i-j)!\)。

对 \(f_i\) 进行化简：

\(f_i=\sum_{j=i-k+1}^i f_{j-1}\times C_{i-1}^{i-j}\times (i-j)!\)
\(=\sum_{j=i-k+1}^i f_{j-1}\times \frac{(i-1)!}{(i-j)!(j-1)!}\times (i-j)!\)
\(=(i-1)!\times \sum_{j=i-k+1}^i \frac{f_{j-1}}{(j-1)!}\)
\(=(i-1)!\times \sum_{j=i-k}^{i-1} \frac{f_j}{j!}\)

令 \(g_i=\frac{f_i}{i!}\)，则 \(g_i=\frac{\sum_{j=i-k}^{i-1} \ \ \ g_j}{i}\)。边计算 \(f_i\) 边维护前缀和。

最后的答案呢?

用相似的方法枚举 \(n\) 所在的位置计算出最终答案为 \(n\) 的排列数，再取个补集。

\(Ans=n!-\sum_{i=1}^n f_{i-1}\times C_{n-1}^{n-i}\times (n-i)!\)
\(=n!-\sum_{i=1}^n g_{i-1}\times (i-1)! \times C_{n-1}^{n-i}\times (n-i)!\)
\(=n!-\sum_{i=1}^n g_{i-1}\times (i-1)! \times \frac{(n-1)!}{(n-i)!(i-1)!}\times (n-i)!\)
\(=n!-(n-1)!\times \sum_{i=1}^n g_{i-1}\)
\(=(n-1)!\times (n-\sum_{i=1}^n g_{i-1})\)

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+5,mod=1e9+7;
int n,k,g[N],f[N],inv[N],sum,ans;
int mul(int x,int n,int mod){
    int ans=mod!=1;
    for(x%=mod;n;n>>=1,x=x*x%mod)
        if(n&1) ans=ans*x%mod;
    return ans;
}
void init(){ 
    int n=1e6;
    f[0]=inv[1]=1;
    for(int i=1;i<=n;i++)
        f[i]=f[i-1]*i%mod;    //fac
    for(int i=2;i<=n;i++)
        inv[i]=(mod-mod/i)*inv[mod%i]%mod;    //inv
    //inv[i] 表示 i 在 mod 1e9+7 意义下的逆元，方便计算 \frac{\sum_{j=i-k}^{i-1} g_j}{i}
} 
signed main(){
    scanf("%lld%lld",&n,&k),init(),g[0]=1,ans=n;
    for(int i=1;i<=n;i++){
        sum=(sum+g[i-1])%mod;
        if(i>k) sum=(sum-g[i-k-1]+mod)%mod;    //\sum_{j=i-k}^{i-1} g_j 
        g[i]=sum*inv[i]%mod;
        ans=(ans-g[i-1]+mod)%mod;    //n-sum{g[i-1]}
    }
    ans=ans*f[n-1]%mod,printf("%lld\n",ans);
    return 0;
}

二、Lucas 定理

1. BZOJ 4403 序列统计

题目大意：给定三个正整数 \(N、L\) 和 \(R\)，统计长度在 \(1\) 到 \(N\) 之间，元素大小都在 \(L\) 到 \(R\) 之间的单调不降序列的数量。输出答案对 \(10^6+3\) 取模的结果。\(1\leq T\leq 100,1\leq N,L,R\leq 10^9\)。

Solution：

\(L,R\) 其实是没用的，直接向左平移 \(L-1\) 个单位就好了。所以区间 \([L,R]\) 等价于 \([1,R-L+1]\)。

考虑枚举长度 \(i\)，并且取值为 \(1\) 到 \(m\)，其中 \(m=R-L+1\)。

转化为插板法。你可以把它看成是，枚举一些板，这些板的意义是，每种元素所到达的最后一个位置。具体来说，比如 \(1,2,3,3,4→\{1\}|\{2\}|\{3,3\}|\{4\}\)。但是 \(1\) 到 \(m\) 这些取值中有一些是可能没有取到的。于是可以在长度为 \(i\) 的序列中再额外加入 \(m\) 个元素，表示我们往每种取值，强制地插入一个元素。这样，\(1\) 到 \(m\) 的每种取值的数个数都大于等于 \(1\) 了，可以直接使用插板法。\(i+m-1\) 个空隙，插 \(m-1\) 个隔板，所以方案数为 \(C_{i+m-1}^{m-1}\)。

\(\sum_{i=1}^n C_{i+m-1}^{m-1}=\sum_{i=1}^n C_{i+m-1}^{m-1}+C_m^m-1\)
\(=\sum_{i=2}^n C_{i+m-1}^{m-1}+C_m^{m-1}+C_m^m-1\)
\(=\sum_{i=2}^n C_{i+m-1}^{m-1}+C_{m+1}^m-1\)（根据杨辉三角的 \(C_n^m=C_{n-1}^m+C_{n-1}^{m-1}\) 可得，以下同理）
\(=\sum_{i=3}^n C_{i+m-1}^{m-1}+C_{m+2}^m-1\)
\(=...\)
\(=\sum_{i=n-1}^n C_{i+m-1}^{m-1}+C_{m+n-2}^m-1\)
\(=\sum_{i=n}^n C_{i+m-1}^{m-1}+C_{m+n-1}^m-1\)
\(=C_{m+n-1}^{m-1}+C_{m+n-1}^m-1\)
\(=C_{m+n}^m-1\)

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+5,mod=1e6+3;
int t,n,m,l,r,f[N],g[N];
int mul(int x,int n,int mod){
    int ans=mod!=1;
    for(x%=mod;n;n>>=1,x=x*x%mod)
        if(n&1) ans=ans*x%mod;
    return ans;
}
void init(){     //预处理阶乘与逆元求组合数 
    int n=mod-1;
    f[0]=g[0]=1;
    for(int i=1;i<=n;i++)
        f[i]=f[i-1]*i%mod;
    g[n]=mul(f[n],mod-2,mod);
    for(int i=n-1;i;i--)
        g[i]=g[i+1]*(i+1)%mod;
} 
int C(int n,int m){
    if(n<m) return 0;    //防止 RE 
    return f[n]*g[m]%mod*g[n-m]%mod;
} 
int lucas(int n,int m,int p){    //Lucas 定理 
    if(!m) return 1;
    return C(n%p,m%p)*lucas(n/p,m/p,p)%p;
}
signed main(){
    scanf("%lld",&t),init();
    while(t--){
        scanf("%lld%lld%lld",&n,&l,&r),m=r-l+1;
        printf("%lld\n",(lucas(m+n,n,mod)%mod-1+mod)%mod);    //C(m+n,n)-1
    }
    return 0;
}

2. BZOJ 4737 组合数问题

题目大意：给定 \(n,m,k\)，求有多少个 \(C_i^j\) 是 \(k\) 的倍数。其中 \(0\leq i\leq n,0\leq j\leq \min(i,m)\)。\(1\leq n,m\leq 10^{18},1\leq t,k\leq 100\)，且 \(k\) 是一个质数。

Solution：

\(\text{Lucas}\) 定理计算 \(C_n^m\) 其实是把 \(n\) 和 \(m\) 表示成 \(p\) 进制数，对 \(p\) 进制下的每一位分别计算组合数，最后再乘起来。

在本题中，我们将 \(i,j\) 看作 \(k\) 进制数，因为要求 \(C_i^j \bmod k=0\)，所以 \(i,j\) 在 \(k\) 进制下的每一位的组合数之积 \(\bmod k=0\)。

因为是 \(k\) 进制数，且 \(k\) 为质数，所以这样的组合数不存在 \(k\) 的因子。所以只要有在 \(k\) 进制下某一位的组合数为 \(0\) 就行了。

只有 \(n<m\) 时，\(C_n^m=0\)。所以必须要求存在某一位，该位上 \(i\) 的数字小于 \(j\) 的数字。于是就可以进行数位 dp 了。

令 \(f_{pos,0/1,0/1,0/1,0/1}\) 表示 dp 到第 \(pos\) 位，是否出现过某一位上 \(i\) 的数字小于 \(j\) 的数字的情况，是否出现过某一位上 \(i\) 的数字大于 \(j\) 的数字的情况，的方案数（后两位表示 \(i,j\) 与上界之间的关系）。

#include<bits/stdc++.h>
#define int long long
#define MEM(x,y) memset(x,y,sizeof(x))
using namespace std;
const int N=70,mod=1e9+7;
int t,k,n,m,f[N][2][2][2][2],a[N],b[N];
int dfs(int i,int flag,int flag2,bool less,bool less2){
    if(!i) return flag;
    if(f[i][flag][flag2][less][less2]!=-1) return f[i][flag][flag2][less][less2];
    int end1=less?a[i]:k-1,end2=less2?b[i]:k-1,ans=0; 
    for(int x=0;x<=end1;x++)    //枚举数位 
        for(int y=0;y<=end2&&(y<=x||flag2);y++)    //y 不能超过 end2，也不能超过 x。如果之前出现过某一位x>y，那么这一位就不需要 y<=x 了。这也就是要记录是否出现过x>y的原因。 
            ans=(ans+dfs(i-1,flag||x<y,flag2||x>y,less&&x==end1,less2&&y==end2)%mod)%mod;
    f[i][flag][flag2][less][less2]=ans;
    return ans;
}
int calc(int x,int y){
    int n=0,m=0;
    while(x) a[++n]=x%k,x/=k;
    while(y) b[++m]=y%k,y/=k;
    while(m<n) b[++m]=0;
    return dfs(n,0,0,1,1);
}
signed main(){
    scanf("%lld%lld",&t,&k);
    while(t--){
        scanf("%lld%lld",&n,&m),MEM(f,-1);
        if(m>n) m=n;
        printf("%lld\n",calc(n,m));
    }
    return 0;
} 

三、容斥原理

1. UVA 11806 Cheerleaders

题目大意：在一个 \(n\times m\) 的矩阵中摆放 \(k\) 个石子，要求第一行、第一列、第 \(m\) 行、第 \(n\) 列必须有石子，求方案总数。\(T\leq 50,n\leq 20,m\leq 20,k\leq 500\)。

Solution：

题目中有四个条件：第一行有石子、第一列有石子、第 \(m\) 行有石子、第 \(n\) 列有石子。

枚举不被满足的条件集合 \(S\) 。若没有条件不被满足的话，总方案数为 \(C_{nm}^k\)。

不被满足集合的大小为 \(1\) 时：以条件一、条件二为例。条件一“第一行有石子”不被满足，意味着“第一行没有石子”，则只有 \(m-1\) 行、\(n\) 列可以放石子，方案数为 \(C_{(m-1)\cdot n}^{k}\)。条件二“第一列有石子”不被满足，意味着“第一列没有石子”，则只有 \(m\) 行、\(n-1\) 列可以放石子，方案数为 \(C_{m\cdot (n-1)}^k\)。其他的同理。

不被满足集合的大小为 \(2\) 时：若条件一与条件三同时不被满足，显然方案数为 \(C_{(m-2)\cdot n}^k\)。若条件三与条件四同时不被满足，显然方案数为 \(C_{(m-1)\cdot (n-1)}^k\)。其余同理。

当不被满足集合的大小为 \(3\) 或者为 \(4\) 的时候，也是可以被类似计算的。

答案为总方案数减去有任意一个条件不被满足的方案数。设 \(A_1\) 为条件一不被满足的方案，\(A_2\) 为条件二不被满足的方案，\(A_3\) 为条件三不被满足的方案，\(A_4\) 为条件四不被满足的方案。

\(Ans=总方案数-\left| \bigcup\limits_{i=1}^{4}A_i \right|\)
\(=C_{nm}^k-(\sum\limits_{i=1}^4\left| A_i \right|-\sum\limits_{1\leq i<j\leq 4}\left|A_i\cap A_j\right|+\sum\limits_{1\leq i<j<k\leq 4}\left|A_i\cap A_j\cap A_k\right|-\sum\limits_{1\leq i<j<k<l\leq 4}\left|A_i\cap A_j\cap A_k\cap A_l\right|)\)

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=510,mod=1e6+7;
int T,t,n,m,k,c[N][N],x,y,cnt,ans;
void init(){    //计算组合数 
    c[0][0]=1;
    for(int i=1;i<=500;i++){
        c[i][0]=1;
        for(int j=1;j<=i;j++)
            c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
    } 
}
signed main(){
    scanf("%lld",&T),init();
    while(T--){
        scanf("%lld%lld%lld",&m,&n,&k),ans=0;
        for(int S=0;S<(1<<4);S++){    //枚举状态 
            x=m,y=n,cnt=0;    //x:可以放棋子的行数  y:可以放棋子的列数  cnt:在当前状态下有几个条件不被满足 
            for(int i=0;i<4;i++)    //枚举条件 
                if((S>>i)&1) (i&1?x--:y--),cnt++;    //如果这个条件不被满足->若是条件一或条件三，那么有一行不能放（即 x--），若是条件二或条件四，那么有一列不能放（即y--） 
            if(!cnt) continue;
            if(cnt&1) ans=(ans+c[x*y][k]%mod)%mod;    //容斥原理，如果有奇数个条件不被满足，就加，反之就减 
            else ans=(ans+mod-c[x*y][k]%mod)%mod; 
        }
        printf("Case %lld: %lld\n",++t,(c[n*m][k]%mod-ans+mod)%mod);    //总方案数减有任意一个条件不被满足的方案数
    } 
    return 0;
} 

2. CF449D Jzzhu and Numbers

题目大意：给出 \(N\) 个数的序列 \(a\)，你需要从这些数当中选出一个非空子集（可含重复元素），使得选出子集的 \(\text{AND}\) 和为零。求方案数。\(N,a_i\leq 10^6\)。

Solution：

看这里 233

四、第二类斯特林数

1. TopCoder 13444 CountTables

题目大意：给出 \(n,m\) 和 \(c\) ，问有多少 \(n\times m\) 的矩阵，矩阵中每个数都在 \([1,c]\) 内，且任两行不完全相同，任两列不完全相同。\(n,m,c\leq 4000\)。

Solution：

先考虑一个子问题。假设并不是有两个条件（任两行不完全相同、任两列不完全相同），而是只有其中一个条件。

假设那一个条件是任意两行不完全相同。那么你可以把一行看作是一个数，对于每一个数，都有 \(c^m\) 种取值（也就是说，有 \(c^m\) 种不同的行），一共有 \(n\) 行。从 \(c^m\) 种取值中选出不相同的 \(n\) 个，方案数为 \(\binom{c^m\ }{n}\cdot n!\)。（因为行之间是有顺序的，所以要乘上 \(n!\)）

令 \(f_i\) 表示 \(n\times i\) 的矩阵满足条件的方案数（第 \(i\) 列的答案）。\(f_m\) 就是答案。

因为需要满足“任两列不完全相同”，所以如果有 \(i\) 列，那么不相同的列的数量就必须为 \(i\)。也就是说，如果不相同的列的数量在 \(1\) 到 \(i-1\) 之间，那么就是不合法的。

考虑枚举不相同的列的数量 \(j\)。把 \(i\) 列看成有 \(i\) 个球，不相同的列的数量 \(j\) 看成 \(j\) 个盒子，把 \(i\) 个球放入 \(j\) 个盒子中，并且盒子要非空，方案数为 \(S(i,j)\cdot f_j\)。（由于第二类斯特林数的盒子之间不区分，所以还要乘上 \(f_j\)。因为如果我们把所有重复出现的列去掉的话，那么就能对应到一个 \(n\times j\) 的矩阵，并且这个矩阵拥有的列都是不相同的，所以乘上 \(f_j\) 就可以解决问题）。

于是可以得到：

\(f_i=\binom{c^i\ }{n}\cdot n!-\sum_{j=1}^{i-1}S(i,j)\cdot f_j\)
\(=\frac{c^i!}{n!(c^i-n)!}\cdot n!-\sum_{j=1}^{i-1}S(i,j)\cdot f_j\)
\(=\frac{c^i!}{(c^i-n)!}-\sum_{j=1}^{i-1}S(i,j)\cdot f_j\)
\(=c^i\times (c^i-1)\times ...\times (c^i-n+1)-\sum_{j=1}^{i-1}S(i,j)\cdot f_j\)

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=4e3+5,mod=1e9+7;
int f[N],s[N][N],x;
class CountTables{
public:
    int howMany(int n,int m,int c){
        s[0][0]=1,x=1;
        for(int i=1;i<=m;i++)
            for(int j=1;j<=i;j++)
                s[i][j]=(s[i-1][j]*j%mod+s[i-1][j-1]%mod)%mod;    //S(i,j)=S(i-1,j)*j+S(i-1,j-1)
        for(int i=1;i<=m;i++){ 
            x=x*c%mod,f[i]=1;    //x:c^i 
            for(int j=1;j<=n;j++)
                f[i]=f[i]*(x-j+1)%mod;
            for(int j=1;j<=i-1;j++)
                f[i]=(f[i]-s[i][j]*f[j]%mod+mod)%mod;
        } 
        return f[m];
    }
}; 
/*
signed main(){
    int n,m,c;
    CountTables ans;
    scanf("%lld%lld%lld",&n,&m,&c);
    printf("%lld\n",ans.howMany(n,m,c));
    return 0;
}*/
#undef int

2. Luogu P4827 Crash 的文明世界

题目大意：给出一棵 \(n\) 个点的树，求对于每个点 \(i\) 的 \(d(i)\) 值。\(d(i)=\sum\limits_{1\leq x\leq n}^{i\neq x}dist(x,i)^k\)。\(1\leq n\leq 50000,1\leq k\leq 150\)。

Solution：

第二类 \(\text{Stirling}\) 数的性质：\(x^n=\displaystyle\sum\limits_{k=0}^n\begin{Bmatrix}n\\k\end{Bmatrix}\dbinom{x}{k}\cdot k!\)

那么，容易得到：

\(d(i)=\displaystyle\sum\limits_{1\leq j\leq n}^{j\neq i}\sum\limits_{p=1}^k \begin{Bmatrix}k\\p\end{Bmatrix}\dbinom{dist(i,j)}{p}\cdot p!=\displaystyle\sum\limits_{p=1}^k p!\begin{Bmatrix}k\\p\end{Bmatrix}\sum\limits_{1\leq j\leq n}^{j\neq i}\dbinom{dist(i,j)}{p}\)

注意到，\(k\) 较小，那么可以直接枚举 \(p\)，\(p!\) 和 \(S(k,p)\) 是可以预处理的。问题转化为处理后面那部分。

令 \(f_{i,p}\) 表示 \(\displaystyle\sum\limits_{1\leq j\leq n}^{j\neq i}\dbinom{dist(i,j)}{p}\)。\(f_{i,p}\) 所统计的对象 \(j\)，包含子树内与子树外。我们先考虑子树内，于是可以令 \(f_{i,p}\) 表示 \(\displaystyle\sum\limits_{j\in subtree(i)}\dbinom{dist(i,j)}{p}\)。

组合数递推式：\(C_{i,j}=C_{i-1,j}+C_{i-1,j-1}\)。

那么，\(\dbinom{dist(i,j)}{p}=\dbinom{dist(i,j)-1}{p}+\dbinom{dist(i,j)-1}{p-1}\)。

则，\(f_{i,p}=\sum\limits_{j\in Son(i)}f_{j,p}+f_{j,p-1}\)。

然后做一遍换根 dp。

稍微提一下换根 dp：假设当前的根是当前节点的父亲，我们下一步需要根换成当前节点。这样就可以一直做下去。具体来说，我们需要做两件事：

• 1. 把当前节点对父亲的贡献，从父亲的 dp 值里扣除（但不能直接修改，因为父亲还有别的儿子，所以我们最好做个备份）。
• 2. 把父亲（除去当前节点的贡献以后，剩余的部分）作为一个新的儿子，加入到当前节点的 dp 值中。这个是要直接修改的，因为要把当前节点换成根。

具体看代码。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e4+5,M=160,mod=1e4+7;
int n,k,x,y,s[M][M],f[M],cnt,hd[N],to[N<<1],nxt[N<<1],dp1[N][M],dp2[N][M],ans,c[N];    //dp1 是子树内的，dp2 是整棵树的 
void add(int x,int y){
    to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt;
}
void dfs1(int x,int fa){
    dp1[x][0]=1;
    for(int i=hd[x];i;i=nxt[i]){
        int y=to[i];
        if(y==fa) continue;
        dfs1(y,x),dp1[x][0]=(dp1[x][0]+dp1[y][0])%mod;
        for(int j=1;j<=k;j++)
            dp1[x][j]=((dp1[x][j]+dp1[y][j])%mod+dp1[y][j-1])%mod;
    }
}
void dfs2(int x,int fa){    //换根 dp 
    for(int i=0;i<=k;i++)
        dp2[x][i]=dp1[x][i];
    if(fa){
        c[0]=(dp2[fa][0]-dp1[x][0]+mod)%mod;
        for(int i=1;i<=k;i++) c[i]=(dp2[fa][i]-dp1[x][i]+mod-dp1[x][i-1]+mod)%mod;    //把当前节点对父亲的贡献，从父亲的 dp 值里扣除
        dp2[x][0]=(dp2[x][0]+c[0])%mod; 
        for(int i=1;i<=k;i++) dp2[x][i]=(dp2[x][i]+c[i]+c[i-1])%mod;    //把父亲作为一个新的儿子，加入到当前节点的 dp 值中 
    }
    for(int i=hd[x];i;i=nxt[i]){
        int y=to[i];
        if(y!=fa) dfs2(y,x);
    }
}
signed main(){
    scanf("%lld%lld",&n,&k),s[0][0]=1,f[0]=1;
    for(int i=1;i<=k;i++)
        for(int j=1;j<=i;j++)
            s[i][j]=(s[i-1][j]*j%mod+s[i-1][j-1])%mod;
    for(int i=1;i<=k;i++)
        f[i]=f[i-1]*i%mod;
    for(int i=1;i<n;i++){
        scanf("%lld%lld",&x,&y);
        add(x,y),add(y,x);
    }
    dfs1(1,0),dfs2(1,0);
    for(int i=1;i<=n;i++){ 
        ans=0;
        for(int p=0;p<=k;p++)
            ans=(ans+f[p]*s[k][p]%mod*dp2[i][p]%mod)%mod;
        printf("%lld\n",ans);
    } 
    return 0;
}

3. CF1278F Cards

题目大意：有 \(n\) 个互相独立的随机变量 \(x_i\)，每个都有 \(\frac{1}{m}\) 的概率为 \(1\)，剩下概率取 \(0\)。求 \(E((\sum\limits_{i=1}^n x_i)^k)\)。\(1\leq n,m<998244353,1\leq k\leq 5000\)。

Solution：

为了方便，我们令 \(p=\frac{1}{m}\)。

考虑枚举随机到 \(1\) 的随机变量的个数。

由于这 \(n\) 个随机变量是互相区分的，如果我们枚举了随机到 \(1\) 的随机变量的个数 \(i\)，那么肯定要乘上 \(n\) 个随机变量中选 \(i\) 个为 \(1\) 的方案数 \(\dbinom{n}{i}\)。选出的 \(i\) 个随机变量，每个有 \(p\) 的概率随机到 \(1\)。剩下的 \(n-i\) 个随机变量，每个都有 \(1-p\) 的概率随机到 \(0\)。所以 \(n\) 个随机变量中，有 \(i\) 个随机到 \(1\) 的概率为 \(p^i\cdot (1-p)^{n-i}\)。此时 \(x_i\) 的和为 \(i\)（\(i\) 个 \(1\)，\(n-i\) 个 \(0\)），所以 \((\sum\limits_{i=1}^n x_i)^k\) 等于 \(i^k\)。则：

\(Ans=\displaystyle\sum\limits_{i=0}^n \dbinom{n}{i}\cdot p^i\cdot (1-p)^{n-i}\cdot i^k\)

根据第二类 \(\text{Stirling}\) 数的性质：\(x^n=\displaystyle\sum\limits_{k=0}^n\begin{Bmatrix}n\\k\end{Bmatrix} x^{\underline k}\)，得

\(Ans=\displaystyle\sum\limits_{i=0}^n \dbinom{n}{i}\cdot p^i\cdot (1-p)^{n-i}\sum\limits_{j=0}^k \begin{Bmatrix}k\\j\end{Bmatrix} i^{\underline j}=\displaystyle\sum\limits_{j=0}^k \begin{Bmatrix}k\\j\end{Bmatrix}\sum\limits_{i=0}^n \dbinom{n}{i}\cdot p^i\cdot (1-p)^{n-i}\cdot i^{\underline j}\)

然后根据下降幂的一个性质：\(\displaystyle\binom{n}{i} i^{\underline j}=\binom{n-j}{i-j} n^{\underline j}\)（为什么？直接展开就行了），得

\(Ans=\displaystyle\sum\limits_{j=0}^k \begin{Bmatrix}k\\j\end{Bmatrix} n^{\underline j}\sum\limits_{i=0}^n \dbinom{n-j}{i-j}\cdot p^i\cdot (1-p)^{n-i}\)
\(=\displaystyle\sum\limits_{j=0}^k \begin{Bmatrix}k\\j\end{Bmatrix} n^{\underline j}\sum\limits_{i=0}^{n-j} \dbinom{n-j}{i}\cdot p^{i+j}\cdot (1-p)^{n-i-j}\)
\(=\displaystyle\sum\limits_{j=0}^k \begin{Bmatrix}k\\j\end{Bmatrix} n^{\underline j}\cdot p^j\sum\limits_{i=0}^{n-j} \dbinom{n-j}{i}\cdot p^i\cdot (1-p)^{n-j-i}\)

因为，\(\displaystyle\sum\limits_{i=0}^{n-j} \dbinom{n-j}{i}\cdot p^i\cdot (1-p)^{n-j-i}=(p+(1-p))^{n-j}=1^{n-j}=1\)（二项式定理），所以 \(Ans=\displaystyle\sum\limits_{j=0}^k \begin{Bmatrix}k\\j\end{Bmatrix} n^{\underline j}\cdot p^j\)。其中，\(n^{\underline j}=\frac{n!}{(n-j)!}=\frac{n\times (n-1)\times ...\times (n-j+1)\times (n-j)\times (n-j-1)\times...\times 1}{(n-j)\times (n-j-1)\times ...\times 1}=n\times (n-1)\times ...\times (n-j+1)\)，可以直接计算。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e3+5,mod=998244353;
int n,m,k,p,f[N],s[N][N],v[N],ans;
int mul(int x,int n,int mod){
    int ans=mod!=1;
    for(x%=mod;n;n>>=1,x=x*x%mod)
        if(n&1) ans=ans*x%mod;
    return ans;
}
signed main(){
    scanf("%lld%lld%lld",&n,&m,&k),p=1*mul(m,mod-2,mod);    //p=1/m
    f[0]=1,s[0][0]=1,v[0]=1;
    for(int i=1;i<=k;i++)
        f[i]=f[i-1]*p%mod;    //f[i]=p^i
    for(int i=1;i<=k;i++)
        for(int j=1;j<=i;j++)
            s[i][j]=(s[i-1][j]*j%mod+s[i-1][j-1]%mod)%mod;
    for(int i=1;i<=k;i++)
        v[i]=v[i-1]*(n-i+1)%mod;    //v[i]=n^{\underline i}
    for(int i=0;i<=k;i++)
        ans=(ans+s[k][i]*v[i]%mod*f[i]%mod)%mod;
    printf("%lld\n",ans);
    return 0;
}

五、图的计数

1. 「ZJOI 2016」小星星

题目大意：给出一棵 \(n\) 个节点的树 \(T\) 和一张 \(n\) 个节点的图 \(G\)。求节点间的对应关系数量使得 \(T\) 为 \(G\) 的一个子图。\(n\leq 17\)。

Solution：

暴力：\(n!\) 枚举映射，再 \(O(n)\) 地判断每条树边是否合法。可以拿到 \(20\%\) 的分数。

子集 DP：

考虑在树 \(T\) 上进行树形 dp。限制在边上，因此有用的信息为:

• 根节点的对应节点
• 子树对应的点集

设计 \(dp_{i,j,k}\) 为以 \(i\) 为根，\(i\) 对应 \(G\) 中节点为 \(j\)，子树对应 \(G\) 中节点集合为 \(k\) 的方案数。

枚举子树时判断 \((u,v)\) 是否在图 \(G\) 中，并做一个子集枚举。

时间复杂度：\(O(3^n n^3)\)。

状压→容斥：

考虑枚举映射到 \(G\) 中的节点集合 \(S\)（或是未出现的节点集合 \(T\))。

使用容斥原理将问题转化为只使用 \(S\) 中节点（不使用 \(T\) 中节点）的合法映射个数。

令 \(dp_{i,j}\) 表示以 \(i\) 为根，\(i\) 映射到 \(G\) 中的节点 \(j\) 时的子树方案数。

使用上个做法当中的树形 dp 即可 \(O(n^3)\) 解决。

时间复杂度：\(O(2^n n^3)\)。

需要进行一定的优化。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=20;
int n,m,x,y,cnt,hd[N],to[N<<1],nxt[N<<1],tot,f[N][N],vis[N],ans;
bool v[N][N];
void add(int x,int y){
    to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt;
}
void dfs(int x,int fa){
    for(int i=1;i<=n;i++) f[x][i]=1;
    for(int i=hd[x];i;i=nxt[i]){
        int y=to[i];
        if(y==fa) continue;
        dfs(y,x);
        for(int j=1;j<=tot;j++){ 
            int sum=0;
            for(int k=1;k<=tot;k++)
                if(v[vis[j]][vis[k]]) sum+=f[y][k];
            f[x][j]*=sum;
        }
    } 
}
signed main(){
    scanf("%lld%lld",&n,&m);
    for(int i=1;i<=m;i++){
        scanf("%lld%lld",&x,&y);
        v[x][y]=v[y][x]=1;    //邻接矩阵 
    }
    for(int i=1;i<n;i++){
        scanf("%lld%lld",&x,&y);
        add(x,y),add(y,x);
    }
    for(int S=0;S<(1<<n);S++){ 
        tot=0; 
        for(int i=0;i<n;i++)
            if((S>>i)&1) vis[++tot]=i+1;    //优化：这样在dfs中就不用1->n枚举点了（改成1->tot） 
        dfs(1,0),tot=n-tot;
        for(int i=1;i<=n;i++){    //容斥 
            if(tot&1) ans-=f[1][i];
            else ans+=f[1][i];
        }
    }
    printf("%lld\n",ans);
    return 0;
}