状态压缩动态规划 状压DP
状态压缩动态规划 状压DP
概念:
- dp的本质是记忆化搜索,而状压dp就如优雅的暴力。
- 状态压缩动态规划,就是我们俗称的状压DP,是利用计算机二进制的性质来描述状态的一种DP方式很多棋盘问题都运用到了状压,同时,状压也很经常和BFS及DP连用,例题里会给出介绍有了状态,DP就比较容易了
举个例子:有一个大小为n*n的农田,我们可以在任意处种田,现在来描述一下某一行的某种状态:
设n = 9;
有二进制数 100011011(九位),每一位表示该农田是否被占用,1表示用了,0表示没用,这样一种状态就被我们表示出来了:见下表
| 列 数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 二进制 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 是否用 | √ | × | × | × | √ | √ | × | √ |
所以我们最多只需要 2n+1−1
的十进制数就好(左边那个数的二进制形式是n个1)
现在我们有了表示状态的方法,但心里也会有些不安:上面用十进制表示二进制的数,枚举了全部的状态,DP起来复杂度岂不是很大?没错,状压其实是一种很暴力的算法,因为他需要遍历每个状态,所以将会出现2^n的情况数量,不过这并不代表这种方法不适用:一些题目可以依照题意,排除不合法的方案,使一行的总方案数大大减少从而减少枚举
位运算
有了状态,我们就需要对状态进行操作或访问
可是问题来了:我们没法对一个十进制下的信息访问其内部存储的二进制信息,怎么办呢?别忘了,操作系统是二进制的,编译器中同样存在一种运算符:位运算 能帮你解决这个问题
(基础,这里不打算手写了,参照这篇博客,以下内容也复制自qxAi的这篇博客,这里谢谢博主)
为了更好的理解状压dp,首先介绍位运算相关的知识。
- & 符号,x&y,会将两个十进制数在二进制下进行与运算,然后返回其十进制下的值。例如3(11)&2(10)=2(10)。
- | 符号,x|y,会将两个十进制数在二进制下进行或运算,然后返回其十进制下的值。例如3(11)|2(10)=3(11)。
- ^ 符号,x^y,会将两个十进制数在二进制下进行异或运算,然后返回其十进制下的值。例如3(11)^2(10)=1(01)。
- << 符号,左移操作,x<<2,将x在二进制下的每一位向左移动两位,最右边用0填充,x<<2相当于让x乘以4。相应的,’>>’是右移操作,x>>1相当于给x/2,去掉x二进制下的最有一位。
这四种运算在状压dp中有着广泛的应用,常见的应用如下:
- 1.判断一个数字x二进制下第i位是不是等于1。
- 方法:if
- 将1左移i-1位,相当于制造了一个只有第i位上是1,其他位上都是0的二进制数。然后与x做与运算,如果结果>0,说明x第i位上是1,反之则是0。
- 2.将一个数字x二进制下第i位更改成1。
- 方法:x=x|(1<<(i−1))
- 证明方法与1类似,此处不再重复证明。
- 3.把一个数字二进制下最靠右的第一个1去掉。
- 方法:x=x&(x−1)
感兴趣的读者可以自行证明。
位运算例题(结合BFS):P2622 关灯问题II
题目描述
现有n盏灯,以及m个按钮。每个按钮可以同时控制这n盏灯——按下了第i个按钮,对于所有的灯都有一个效果。按下i按钮对于第j盏灯,是下面3中效果之一:如果a[i][j]为1,那么当这盏灯开了的时候,把它关上,否则不管;如果为-1的话,如果这盏灯是关的,那么把它打开,否则也不管;如果是0,无论这灯是否开,都不管。
现在这些灯都是开的,给出所有开关对所有灯的控制效果,求问最少要按几下按钮才能全部关掉。
输入输出格式
输入格式:
- 前两行两个数,n m接下来m行,每行n个数,a[i][j]表示第i个开关对第j个灯的效果。
- 输出格式:一个整数,表示最少按按钮次数。如果没有任何办法使其全部关闭,输出-1
这题需要对状压及位运算有一定的了解:首先要判断某一位的灯是开的还是关的,才能进行修改。
具体解法是:对队首的某一状态,枚举每一个开关灯操作,记录到达这一新状态的步数(也就是老状态 + 1),若是最终答案,输出,若不是,压入队列。
也就是说:我们把初始状态,用每个操作都试一遍,就产生了许多新的状态,再用所有操作一一操作新状态,就又产生了新的新状态,我们逐一尝试,直到有目标状态为止,这可以通过BFS实现。
所以现在知道为什么状压比较暴力了吧。

#include<iostream> #include<vector> #include<queue> #include<cstdio> #include<cstring> using namespace std; int RD(){ int out = 0,flag = 1;char c = getchar(); while(c < '0' || c >'9'){if(c == '-')flag = -1;c = getchar();} while(c >= '0' && c <= '9'){out = out * 10 + c - '0';c = getchar();} return flag * out; } const int maxn = 2048; int num,m,numd; struct Node{ int dp,step; }; int vis[maxn]; int map[maxn][maxn]; void BFS(int n){ queue<Node>Q; Node fir;fir.step = 0,fir.dp = n;//初始状态入队 Q.push(fir); while(!Q.empty()){//BFS Node u = Q.front(); Q.pop(); int pre = u.dp; for(int i = 1;i <= m;i++){//枚举每个操作 int now = pre; for(int j = 1;j <= num;j++){ if(map[i][j] == 1){ if( (1 << (j - 1)) & now){ now = now ^ (1 << (j - 1));//对状态进行操作 } } else if(map[i][j] == -1){ now = ( (1 << (j - 1) ) | now);//对状态进行操作 } } fir.dp = now,fir.step = u.step + 1;//记录步数 if(vis[now] == true){ continue; } if(fir.dp == 0){//达到目标状态 vis[0] = true;//相当于一个标记flag cout<<fir.step<<endl;//输出 return ;//退出函数 } Q.push(fir);//新状态入队 vis[now] = true;//表示这个状态操作过了(以后在有这个状态就不用试了) } } } int main(){ num = RD();m = RD(); int n = (1 << (num)) - 1; for(int i = 1;i <= m;i++){ for(int j = 1;j <= num;j++){ map[i][j] = RD(); } } BFS(n); if(vis[0] == false) cout<<-1<<endl; return 0; }
状压 + DP = 状压DP
同样也是一种挺暴力的DP方式,我们直接看题吧
P1879 [USACO06NOV]玉米田Corn Fields
题目描述
Farmer John has purchased a lush new rectangular pasture composed of M by N (1 ≤ M ≤ 12; 1 ≤ N ≤ 12) square parcels. He wants to grow some yummy corn for the cows on a number of squares. Regrettably, some of the squares are infertile and can't be planted. Canny FJ knows that the cows dislike eating close to each other, so when choosing which squares to plant, he avoids choosing squares that are adjacent; no two chosen squares share an edge. He has not yet made the final choice as to which squares to plant.
Being a very open-minded man, Farmer John wants to consider all possible options for how to choose the squares for planting. He is so open-minded that he considers choosing no squares as a valid option! Please help Farmer John determine the number of ways he can choose the squares to plant.
农场主John新买了一块长方形的新牧场,这块牧场被划分成M行N列(1 ≤ M ≤ 12; 1 ≤ N ≤ 12),每一格都是一块正方形的土地。John打算在牧场上的某几格里种上美味的草,供他的奶牛们享用。
遗憾的是,有些土地相当贫瘠,不能用来种草。并且,奶牛们喜欢独占一块草地的感觉,于是John不会选择两块相邻的土地,也就是说,没有哪两块草地有公共边。
John想知道,如果不考虑草地的总块数,那么,一共有多少种种植方案可供他选择?(当然,把新牧场完全荒废也是一种方案)
输入输出格式
输入格式:
第一行:两个整数M和N,用空格隔开。
第2到第M+1行:每行包含N个用空格隔开的整数,描述了每块土地的状态。第i+1行描述了第i行的土地,所有整数均为0或1,是1的话,表示这块土地足够肥沃,0则表示这块土地不适合种草。
输出格式:
一个整数,即牧场分配总方案数除以100,000,000的余数。
其实这题是可以减少状态来达到减少复杂度的,可是我写着题的时候还不会。。。关于减少复杂度可以看下面一篇例题
这题也是用二进制来表示状态,先预处理:枚举一行内(不考虑地图因素)每一种状态,看看是否合法,合法的话就打个标记(其实这里可以减状态数的那时候还不知道QAQ),以便后面操作,最后先处理第一行,枚举下面行的时候再枚举一遍上一行,看看两行放置是否合法,合法就累计上一行计数即可。
#include<iostream> #include<vector> #include<queue> #include<cstdio> #include<cstring> using namespace std; int RD(){ int out = 0,flag = 1;char c = getchar(); while(c < '0' || c >'9'){if(c == '-')flag = -1;c = getchar();} while(c >= '0' && c <= '9'){out = out * 10 + c - '0';c = getchar();} return flag * out; } const int maxn = 4096,M = 100000000; int n,m; int tmap[19][19]; int map[19]; int dp[19][maxn]; bool can[maxn]; int main(){ n = RD(),m = RD(); for(int i = 1;i <= n;i++){ for(int j = 1;j <= m;j++){ tmap[i][j] = RD(); map[i] = (map[i] << 1) + tmap[i][j];//利用把地图变为二进制的形式可以快速计算是否合法,要对位运算熟悉掌握 } } int maxstate = (1 << m) - 1;//最大状态数 for(int i = 0;i <= maxstate;i++){ if((((i << 1) & i) == 0) & (((i >> 1) & i) == 0)){ can[i] = true;//后面有更优的写法,看下一篇题目 } } for(int i = 0;i <= maxstate;i++){ if((can[i]) & ((i & map[1]) == i)){ dp[1][i] = 1;//先预处理出第一行(对于某一行的状态,只受上一行影响) } } for(int i = 2;i <= n;i++){ for(int j = 0;j <= maxstate;j++){ if((can[j]) & (j & map[i]) == j){ for(int k = 0;k <= maxstate;k++){ if((k & j) == 0){ dp[i][j] = (dp[i][j] + dp[i - 1][k]) % M;//dp过程 } } } } } long long ans = 0; for(int i = 0;i <= maxstate;i++){ ans = (ans + dp[n][i]) % M;//答案在最后一行 } cout<<ans<<endl; return 0; }
P1896 [SCOI2005]互不侵犯King
题目描述
在N×N的棋盘里面放K个国王,使他们互不攻击,共有多少种摆放方案。国王能攻击到它上下左右,以及左上左下右上右下八个方向上附近的各一个格子,共8个格子。
输入输出格式
输入格式:
只有一行,包含两个数N,K ( 1 <=N <=9, 0 <= K <= N * N)
输出格式:
所得的方案数
题目十分简短:观察数据范围我们可以知道:这题有庞大的状态量,所以我们就用状压DP解决问题
dp思路:三维,第一维表示行数,第二维表示状态(二进制),第三维表示已经放了的棋子数(说实话做题做多了会有套路的,有数量限制的dp一般都要开一维表示用了的数量)
直接上代码:

#include<iostream> #include<vector> #include<queue> #include<cstdio> #include<cstring> #define ll long long using namespace std; int RD(){ int out = 0,flag = 1;char c = getchar(); while(c < '0' || c >'9'){if(c == '-')flag = -1;c = getchar();} while(c >= '0' && c <= '9'){out = out * 10 + c - '0';c = getchar();} return flag * out; } int len,k; ll dp[19][1024][110]; int need[1024];//表示每种状态用的棋子数 bool can[1024]; int main(){ len = RD();k = RD(); int maxstate = (1 << len) - 1; for(int i = 0;i <= maxstate;i++){ int temp = i; while(temp != 0){ if(temp % 2 == 1)need[i] += 1;//处理所需棋子数 temp /= 2; } } for(int i = 0;i <= maxstate;i++){ if(((i << 1) & i) == 0){ can[i] = true;//处理一行内不冲突的情况 } } for(int i = 0;i <= maxstate;i++){ if(can[i] & need[i] <= k)dp[1][i][need[i]] = 1;//预处理第一行 } for(int i = 2;i <= len;i++){ for(int j = 0;j <= maxstate;j++){ if(can[j]){ for(int s = 0;s <= maxstate;s++){ if(can[s] == false)continue; if((s & j) != 0)continue;//正面上我啊 if(((s << 1) & j) != 0)continue;//左边上我啊 if(((s >> 1) & j) != 0)continue;//右边上我啊 for(int l = k;l >= need[j];l--){ dp[i][j][l] += dp[i - 1][s][l - need[j]]; } } } } } ll ans = 0; for(int i = 0;i <= maxstate;i++){ ans += dp[len][i][k]; } cout<<ans<<endl; return 0; }
通过题目要求减少状态量
这可以说是状压的一大精华了。一般状压的题目会有大量的状态,枚举所有状态则需要大量的时间,时间承受不了,若和dp结合起来,dp数组开个三四维,空间也吃不消。
所以我们可以通过预处理状态,去掉不合法的状态,减少时空的需要
具体实现和STL中的map很相似:我们用一个序号来映射状态,开一个数组INDEX[ ](这里有坑,小写的index会和cstring库冲突,如果给用的话我绝对用小写魔禁万岁!!!(虽然我站上琴) )INDEX[i]表示第i个合法的状态是什么,然后枚举的时候直接枚举INDEX数组就好了
P2704 [NOI2001]炮兵阵地
题目描述
司令部的将军们打算在NM的网格地图上部署他们的炮兵部队。一个NM的地图由N行M列组成,地图的每一格可能是山地(用“H” 表示),也可能是平原(用“P”表示),如下图。在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示:
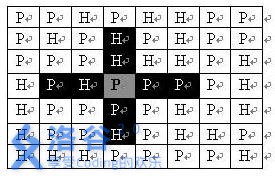
如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。 现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。
输入输出格式
输入格式:
第一行包含两个由空格分割开的正整数,分别表示N和M;
接下来的N行,每一行含有连续的M个字符(‘P’或者‘H’),中间没有空格。按顺序表示地图中每一行的数据。N≤100;M≤10。
输出格式:
仅一行,包含一个整数K,表示最多能摆放的炮兵部队的数量。
自己推一下就可以发现,判断此行是否合法需要枚举上一行和上两行的状态,(dp要开三维:第一维表示行数,第二维表示现在枚举的状态,第三维表示上一行的状态,所以dp[i][j][k]表示第i行排成j个状态,且上一行状态是k的最大数量),直接枚举所有状态是肯定会超时的,这时候我们就需要通过题目要求减少状态量了。
减少状态量做法上面已经提过了,其他做法与普通状压类似。
总结一下此类题目的dp方法(玉米田也是这类问题):若某个状态可以对下n行的状态造成影响,那么就要预处理前n行合法的,对于n + 1行及以后,判断某状态是否合法需要往上枚举n行,所以dp数组要开n + 1维,第一维表示行数,第二维表示现在的状态,再往后第n维表示上n - 2行的状态(其实不可能出太多行的,时间指数增长)
这样dp就这样进行:
for(所有状态)
for(所有状态)
...{向上枚举n行}
dp[i][j][k][l]...[n + 1] += dp[i - 1][k][l]...[最上面一行];
//求最大方案数就max()
//意会吧,不怎么讲得清楚AC代码:

#include<iostream> #include<vector> #include<queue> #include<cstdio> #include<cstring> #define ll long long using namespace std; int RD(){ int out = 0,flag = 1;char c = getchar(); while(c < '0' || c >'9'){if(c == '-')flag = -1;c = getchar();} while(c >= '0' && c <= '9'){out = out * 10 + c - '0';c = getchar();} return flag * out; } const int maxn = 110; int lenx,leny; ll dp[110][maxn][maxn]; bool can[maxn]; bool cann[110][maxn]; int tmap[110][19]; int map[maxn]; int put[maxn]; int INDEX[maxn]; int cnt; char in; int main(){ lenx = RD();leny = RD(); for(int i = 1;i <= lenx;i++){ for(int j = 1;j <= leny;j++){ cin>>in; if(in == 'P')tmap[i][j] = 1; } } for(int i = 1;i <= lenx;i++){ for(int j = 1;j <= leny;j++){ map[i] = (map[i] << 1) + tmap[i][j];//和玉米田类似,处理为二进制地图 } } int maxstate = (1 << leny) - 1; for(int i = 0;i <= maxstate;i++){//枚举一行里的状态 if((((i << 1) & i) == 0) & (((i << 2) & i) == 0)){ INDEX[++cnt] = i;//合法的存在INDEX里,最终cnt表示合法方案数 can[cnt] = true; int temp = i; while(temp != 0){ if(temp % 2 == 1){put[cnt] += 1;} temp /= 2; } } } for(int i = 1;i <= cnt;i++){//第一行 if(can[i] & ((INDEX[i] & map[1]) == INDEX[i])){ cann[1][i] = true; dp[1][i][0] = put[i]; } } for(int i = 1;i <= cnt;i++){ if(can[i] & ((INDEX[i] & map[2]) == INDEX[i])){//选一个第二行合法的 cann[2][i] = true;//标记一下合法,减少再计算 for(int j = 1;j <= cnt;j++){//在第一行找一个 if(!cann[1][j])continue;//要在第一行合法 if((INDEX[i] & INDEX[j]) == 0){//还要不与第二行冲突 dp[2][i][j] = max(dp[2][i][j],dp[1][j][0] + put[i]); } } } } for(int i = 3;i <= lenx;i++){ for(int j = 1;j <= cnt;j++){ if(can[j] & ((INDEX[j] & map[i]) == INDEX[j])){ cann[i][j] = true; for(int k = 1;k <= cnt;k++){//枚举上两行状态 if(!cann[i - 2][k])continue; if(!((INDEX[j] & INDEX[k]) == 0))continue; for(int l = 1;l <= cnt;l++){ if(!cann[i - 1][l])continue;//枚举上一行状态 if(((INDEX[j] & INDEX[l]) != 0) || ((INDEX[k] & INDEX[l]) != 0))continue; dp[i][j][l] = max(dp[i][j][l],dp[i - 1][l][k] + put[j]); } } } } } ll ans = 0; for(int i = 1;i <= cnt;i++){ for(int j = 1;j <= cnt;j++){ ans = max(ans,dp[lenx][i][j]); } } cout<<ans<<endl; return 0; }



