LCA (Least Common Ancestors)

LCA（Least Common Ancestors）

是解决很多树上问题都必须应用到的东西。
对于点集 S = a1, a2, ..., an 的最近公共祖先 LCAS 为 S 的所有公共祖先中深度最深的那个。
即最近公共祖先，是指在有根树中，找出某两个结点u和v最近的公共祖先。对于有根树T的两个结点u、v，最近公共祖先表示一个结点x，满足x是u、v的祖先且x的深度尽可能大。
另一种理解方式是把T理解为一个无向无环图，而即u到v的最短路上深度最小的点。这里给出几个LCA的例子：
常用结论转化：多个点的 LCA 即这些点中 dfs 序（仅考虑进栈序）最大者和最小者的 LCA。所以求解多个点 LCAS 的问题可以简单规约为求解两点 LCAu,v 的问题，常见解法如下。

　　▶ 朴素暴力

　　▶ 倍增法

　　▶ 规约为 RMQ 问题(思考)

　　▶ Tarjan 算法

对于

则有:

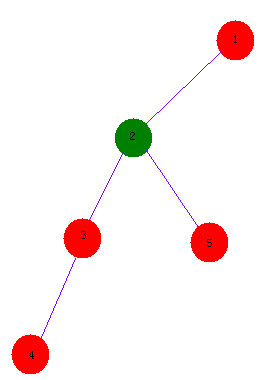
4和5的LCA就是2

　　那怎么求呢？最粗暴的方法就是先dfs一次，处理出每个点的深度

实现

暴力枚举（朴素算法）

对于有根树T的两个结点u、v，首先将u，v中深度较深的那一个点向上蹦到和深度较浅的点，然后两个点一起向上蹦，直到蹦到同一个点，这个点就是u，v的最近公共祖先，记作LCA（u，v）。但是这种方法的时间复杂度在极端情况下会达到。特别是有多组数据求解时，时间复杂度将会达到O（n*m）。

#include<bits/stdc++.h>
using namespace std;
int f[100010][31];
int n,q,x,y,tot,root;
struct edge{
    int to;
    int nxt;
    int dis;
}e[100010];
int head[100010];
void add_edge(int x,int y)
{
    e[++tot].nxt=head[x];
    head[x]=tot;
    e[tot].to=y;
    e[++tot].nxt=head[y];
    head[y]=tot;
    e[tot].to=x;
}
void Deal_first(int x,int root)
{
    e[x].dis=e[root].dis+1;
    for(int i=0;i<=20;i++)
        f[x][i+1]=f[f[x][i]][i];
    for(int i=head[x];i;i=e[i].nxt)
    {
        int to=e[i].to;
        if(to==root)continue;
        f[to][0]=x;
        Deal_first(to,x);
    }
}
int LCA(int x,int y)
{
      if(e[x].dis<e[y].dis)swap(x,y);
      for(int i=20;i>=0;i--)
      {
          if(e[f[x][i]].dis>=e[y].dis)x=f[x][i];
          if(x==y)return x;
      }
      for(int i=20;i>=0;i--)
      {
          if(f[x][i]!=f[y][i])
          {
              x=f[x][i];
              y=f[y][i];
          }
      }
      return f[x][0];
  }
int dist(int x,int y)
{
        return e[x].dis+e[y].dis-2*e[LCA(x,y)].dis;
}
int main()
{
      scanf("%d",&n);
      for(int i=1;i< n;i++)
      {
          scanf("%d%d",&x,&y);
          add_edge(x,y);
      }
      Deal_first(1,0); 
      scanf("%d",&q);
      while(q--)
      {
          scanf("%d%d",&x,&y);
          printf("%d\n",dist(x,y));
      }
}

Lca Code

当然我我们一定有简单一点的算法

这里我们就要引入传说中的倍增LCA
他就是相当于2进制拆分的一个过程，先把u，v换到统一层在一起往上跳。
这个复杂度是$O(logn)$的。

int lca(int u,int v)
{
    u-maxdeep(u,v);
    for(int i=20;i>=1;i--)
        if(deep[anc[u][i]]>=deep[v])u=anc[u][i];
    //保证u,v deep相同
    for(int i=20;i>=0;i--)
    {
        if(anc[u][i]!=anc[v][i])
            u=anc[u][i],v=anc[v][i];
    }
    return anc[u][0];
}

View Code

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5;
int n,m,root;
struct edge{
    int to;
    int nxt;
}e[N];
int head[N],tot;
int dep[N],fa[N][22],lg[N];
void addedge(int x,int y)
{
    e[++tot].to=y;
    e[tot].nxt=head[x];
    head[x]=tot;
}
void superadd(int x,int y)
{
    addedge(x,y);
    addedge(y,x);
}
void dfs(int x,int ffa)
{
    dep[x]=dep[ffa]+1;
    fa[x][0]=ffa;
    for(int i=1;1<<i<=dep[x];i++)
        fa[x][i]=fa[fa[x][i-1]][i-1];
    for(int i=head[x];i;i=e[i].nxt)
    {
        int v=e[i].to;
        if(v!=ffa)dfs(v,x);
    }
}
int lca(int x,int y)
{
    if(dep[x]<dep[y])swap(x,y);
    while(dep[x]>dep[y])x=fa[x][lg[dep[x]-dep[y]]-1];
    if(x==y)return x;
    for(int i=lg[dep[x]];i>=0;i--)
        if(fa[x][i]!=fa[y][i]){x=fa[x][i];y=fa[y][i];}
    return fa[x][0];
}
inline int read()
{
    int x=1,f=0;
    char ch=getchar();
    while(ch<'0'||ch>'9'){x=ch=='-'?-1:1;ch=getchar();}
    while(ch>='0'&&ch<='9'){f=(f<<1)+(f<<3)+(ch^48);ch=getchar();}
    return x*f;
}
int main()
{
    n=read();
    m=read();
    for(int i=1,u,v;i<n;i++)
    {
        u=read();
        v=read();
        superadd(u,v);
    }
    dfs(1,0);
    for(int i=1;i<=n;i++)
        lg[i]=lg[i-1]+(1<<lg[i-1]==i);
    for(int i=1,a,b,c;i<=m;i++)
    {
        a=read();
        b=read();
        int ans=lca(a,b);
        printf("%d\n",ans);
    }
}

View Code

RMQ请阅读：

https://www.cnblogs.com/liuhailin/p/11019502.html

Tarjan离线求LCA

这个算法需要建两棵树，88行
它是一个类似于灌水的算法，首先从最左下角的叶子节点向里灌水，水慢慢向上蔓延我们把要求的两点编号看成浮标跟着水向上跑，直到两点相遇在同一个节点。因为是从下往上跑所以最先相遇的点一定是最深的，即最优解。显然正确性是可以保证的。

#include<bits/stdc++.h>
using namespace std;
const int N=3e6+3;
int n,m;
bool vis[N];
struct edge{
    int to;
    int nxt;
}e[2*N];
int head[N],tot;
struct node{
    int lca;
    int to;
    int nxt;
}f[2*N];
int hwd[N],kk;
void edgeadd(int x,int y)
{
    f[++kk].to=y;
    f[kk].nxt=hwd[x];
    hwd[x]=kk;
}
int fa[N];
int find(int x)
{
    if(fa[x]!=x)
        fa[x]=find(fa[x]);
    return fa[x];
}
void addedge(int x,int y)
{
    e[++tot].to=y;
    e[tot].nxt=head[x];
    head[x]=tot;
}
void dfs(int x)
{
    vis[x]=true;
    for(int i=head[x];i;i=e[i].nxt)
    {
        int v=e[i].to;
        if(vis[v])continue;;
        dfs(v);
        fa[v]=x;
    }
    for(int i=hwd[x];i;i=f[i].nxt)
    {
        int v=f[i].to;
        if(vis[v])
        {
            f[i].lca=find(v);
            if(i&1)f[i+1].lca=f[i].lca;
            else f[i-1].lca=f[i].lca;
        } 
    }
}
inline int read()
{
    int x=1,f=0;
    char ch=getchar();
    while(ch<'0'||ch>'9'){x=ch=='-'?-1:1;ch=getchar();}
    while(ch>='0'&&ch<='9'){f=(f<<1)+(f<<3)+(ch^48);ch=getchar();}
    return x*f;
}
int main()
{
    n=read();
    int st;
    for(int i=1;i<=n;i++)fa[i]=i;
    for(int i=1,x;i<=n;i++)
    {
        x=read();
        if(!x)st=i;
        addedge(x,i);
        addedge(i,x);
    }
    m=read();
    for(int i=1,x,y;i<=m;i++)
    {
        x=read();
        y=read();
        edgeadd(x,y);
        edgeadd(y,x);
    }
    dfs(st);
    for(int i=1;i<=m;i++)
        printf("%d\n",f[2*i].lca);
}

Tarjan Code

Thanks-------

posted @ 2019-07-26 20:11 milkitblogcn 阅读(374) 评论(0) 编辑收藏举报

刷新页面返回顶部

mlkitblogcn