【清北学堂2018-刷题冲刺】Contest 4
Task 1:序列
【问题描述】
小H原本有一个由连续的正整数组成的序列,如{4,5,6}或{10,11,12,13,14,15,16},但是她最近睡眠不足,只能记得其中的一些数字。她想知道,她最少可能只忘了多少数字。
【输入】
第一行一个整数N表示小H记得的数的个数。
第二行N个正整数Ai表示小H记得的数,保证Ai互不相同但是以打乱的顺序给出。
【输出】
一行一个整数表示答案。
【输入输出样例】
4 10 13 12 8
2
【样例解释】
可能的原序列是{8,9,10,11,12,13},小H只忘记了{9,11}两个数。
【数据范围】
-
1 – 4 1 ≤ N,Ai ≤ 100
-
5 – 8 1 ≤ N,Ai ≤ 1000
-
9 - 10 1 ≤ N ≤ 106,1 ≤ Ai ≤10^9
傻X题,直接水过。数据范围的话,N的范围实际上有点危险,建议手写max,min+快读。
#include<cstdio>
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x<y?x:y;}
inline int read(){
int s=0;
char ch=getchar();
while('9'<ch||ch<'0'){
ch=getchar();
}
while('0'<=ch&&ch<='9'){
s=s*10+ch-'0';
ch=getchar();
}
return s;
}
int main(){
freopen("sequence.in","r",stdin);
freopen("sequence.out","w",stdout);
int maxn=0,minn=0x3f3f3f3f,n=read();
register int tmp;
for(register int i=1;i<=n;++i){
tmp=read();
maxn=max(maxn,tmp);
minn=min(minn,tmp);
}
printf("%d\n",maxn-minn-n+1);
return 0;
}
Task 2:食物
【问题描述】
小H喜欢吃肉、鱼和巧克力,但她不喜欢某些食用的顺序。
小H每小时都会吃肉、鱼和巧克力其中一种。但如果出现以下情况,她就会不开心:
-
有连续3小时吃同一种食物。
-
有连续3小时她吃了所有种类的食物且中间那小时吃的是巧克力。
-
有连续3小时她在中间那小时吃了肉或鱼而此外的两小时吃的是巧克力。
小H想知道,有多少种吃东西的序列能让自己在连续N个小时保持开心。
你只需要输出答案对1000000007取模后的值。
【输入】
第一行一个整数T表示数据组数。
接下来T行每行一个整数N。
【输出】
对于每组数据输出一行一个整数表示答案。
【输入输出样例】
3 3 4 15
20 46 435170
【数据范围】
- 1 – 6 1 ≤ N ≤ 10^6
- 7 – 10 1 ≤ N ≤ 10^9
对于这个题目来说,搜索很显然是不可能跑得动的。
先考虑最直观的想法:直接DP,进行转移。复杂度O(nT)。
设三种食物分别为1,2,3,那么有几种情况是不可用的:
-
1 1 1
-
2 2 2
-
3 3 3
-
1 3 2
-
2 3 1
-
3 1 3
-
3 2 3
排除这些情况,其他的直接进行转移即可。
但是很显然1e9的总复杂度再带上一个不小的常数是不可能跑过去的,60pts都没有。这是我们会发现:输入只有一个变量,而询问有1000次。我们考虑O(n)预处理优化一下,提前存储答案,就有了60pts。
100pts的写法呢?看到1e9的数据就应该意识到这是一个矩阵加速递推的题目
首先我们把3x3的状态压缩成1x9来看看最初的转移:
.png)
我们的转移就这样变成了可以被矩阵优化的形式,接下来的操作就变得自然而然:构造一个9x9的矩阵。
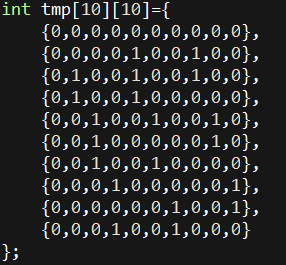
经过大力构造,我们就得到了这样一个东西:
按照我们构造时候的定义,答案矩阵就是初始矩阵*tmp^(n-2)了,矩阵快速幂大力跑过去,100pts到手。
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int mod=1000000007;
int tmp[10][10]={
{0,0,0,0,0,0,0,0,0,0},
{0,0,0,0,1,0,0,1,0,0},
{0,1,0,0,1,0,0,1,0,0},
{0,1,0,0,1,0,0,0,0,0},
{0,0,1,0,0,1,0,0,1,0},
{0,0,1,0,0,0,0,0,1,0},
{0,0,1,0,0,1,0,0,0,0},
{0,0,0,1,0,0,0,0,0,1},
{0,0,0,0,0,0,1,0,0,1},
{0,0,0,1,0,0,1,0,0,0}
};
int bg[2][10]={
{0,0,0,0,0,0,0,0,0,0},
{0,1,1,1,1,1,1,1,1,1}
};//state of begin
struct Matrix{
int mp[10][10];
void Init(){
memset(mp,0,sizeof(mp));
}
void Unit(){
memset(mp,0,sizeof(mp));
for(int i=1;i<=9;++i){
mp[i][i]=1;
}
}
};
Matrix __mul(Matrix x,Matrix y){
Matrix ans;
ans.Init();
for(register int i=1;i<=9;++i){
for(register int j=1;j<=9;++j){
for(register int k=1;k<=9;++k){
ans.mp[i][k]=(ans.mp[i][k]+(long long)x.mp[i][j]*y.mp[j][k])%mod;
}
}
}
return ans;
}
Matrix __pow(Matrix tmp,int p){
Matrix ans;
ans.Unit();//initialize
while(p){
if(p&1){
p^=1;
ans=__mul(ans,tmp);
}
p>>=1;
tmp=__mul(tmp,tmp);
}
return ans;
}
int main(){
freopen("food.in","r",stdin);
freopen("food.out","w",stdout);
Matrix mat;
for(int i=0;i<=9;++i){
for(int j=0;j<=9;++j){
mat.mp[i][j]=tmp[i][j];
}
}
int T,n;
scanf("%d",&T);
while(T--){
scanf("%d",&n);
Matrix res=__pow(mat,n-2),ans;
ans.Init();
for(int i=1;i<=1;++i){
for(int j=1;j<=9;++j){
for(int k=1;k<=9;++k){
ans.mp[i][k]=(ans.mp[i][k]+(long long)bg[i][j]*res.mp[j][k])%mod;
}
}
}
int anss=0;
for(int i=1;i<=9;++i){
anss=(anss+ans.mp[1][i])%mod;
}
printf("%d\n",anss);
}
return 0;
}
Task 3:雪
【问题描述】
小H喜欢堆雪堆,在一共N天的寒假里,她在第i天会堆一个体积为Vi的雪堆。
雪堆每天都会融化一部分,准确地讲,如果这天的气温是Ti,那么每个堆好的雪堆的体积都会减少Ti。如果某个雪堆的体积减到了0,那么它便会消失。
小H想知道每天总共融化的雪的体积是多少。
【输入】
第一行为1个正整数N。
第二行为N个正整数Vi。
第三行为N个整整数Ti。
【输出】
共N行每行一个整数表示当天融化的雪的总体积。
【输入输出样例】
5
30 25 20 15 10
9 10 12 4 13
ans:9 20 35 11 25
【数据范围】
- 1 – 4 1 ≤ N ≤ 100
- 5 - 6 1 ≤ N ≤ 1000
- 7 - 10 1 ≤ N ≤ 100000
对于100%的数据:0 ≤ Vi, Ti ≤ 109。
大水题,没有想象中那么复杂,直观想法就可以跑过去。
维护气温的前缀和,二分答案找到第i天堆的雪人会在哪天化掉。在这一天特殊处理,其他天都是完整的化掉一个气温大小的体积,所以丢进树状数组差分维护即可。
树状数组大法吼啊!!!
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 100010
#define lint long long
using namespace std;
lint n,V[MAXN],T[MAXN],sum[MAXN],ans[MAXN],Tree[MAXN];
inline lint read(){
lint s=0;
char ch=getchar();
while('9'<ch||ch<'0'){
ch=getchar();
}
while('0'<=ch&&ch<='9'){
s=s*10+ch-'0';
ch=getchar();
}
return s;
}
inline lint lowbit(lint x){
return x&-x;
}
inline void add(lint pos,lint val){
while(pos<=n){
Tree[pos]+=val;
pos+=lowbit(pos);
}
}
inline lint getsum(lint pos){
lint ans=0;
while(pos){
ans+=Tree[pos];
pos-=lowbit(pos);
}
return ans;
}
int main(){
freopen("snow.in","r",stdin);
freopen("snow.out","w",stdout);
n=read();
for(register int i=1;i<=n;++i){
V[i]=read();
}
for(register int i=1;i<=n;++i){
T[i]=read();
sum[i]=sum[i-1]+T[i];
//维护一个时间的前缀和
}
for(register int i=1;i<=n;++i){
//day i:build V[i],melt T[i]
lint pos=lower_bound(sum+1,sum+1+n,V[i]+sum[i-1])-sum;
ans[pos]+=V[i]-(sum[pos-1]-sum[i-1]);
add(i,1);
add(pos,-1);
}
for(register int i=1;i<=n;++i){
ans[i]+=getsum(i)*T[i];
printf("%lld ",ans[i]);
}
return 0;
}