后缀自动机多图详解（代码实现）

作者注：搭配理论证明类的\(SAM\)博客阅读，效果更佳。作者水平较低，时间有限，只讲实现，不再胡乱证明。

后缀自动机是一种在线的，动态添加字符扩展字符串的算法。蒟蒻深知没图的痛苦，这里放一个带详细图片解析的代码实现，加深一下自己印象。顺便造福后人

作图工具：\(WPS\) \(PowerPoint\) \(For\) \(Ubuntu\)

如图所示，添加扩展字符\(c\)后，后缀自动机中受影响的有且仅有\(p\)的后缀，所以我们只需对\(p\)的后缀的连边情况进行更新即可。

  • 遍历\(p\)的后缀。（\(=\)在其后缀链接\(/\)\(parent\) \(Tree\)上向上跳）

    • \(p\)的后缀中有一部分，其后面接上字符\(c\)获得的新后缀，在添加字符\(c\)之前的原串中还未出现过。虽然原串中并没有这样的串，但是添加字符\(c\)后的新串中就刚刚出现了一个。这里我们拉一条向新串\(q\)的，字符为\(c\)的\(Trie\)边。

int p = lst, q = ++node; lst = q;
len[q] = len[p] + 1;
while (!ch[p][c] && p != 0) {
    ch[p][c] = q;
    p = fa[p];//更新原串后缀的连边
}

  • 通过这一步，我们完成了图示中下面一部分的状态更新。

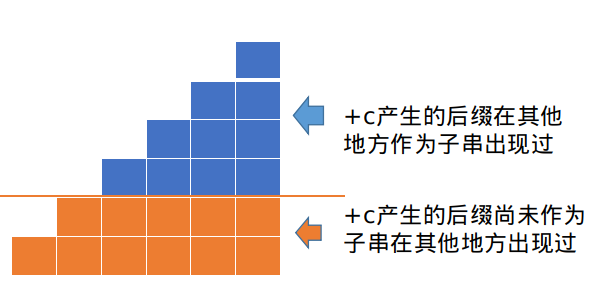
对上面的那一部分，我们要分类讨论。

  1. 字符\(c\)是第一次出现

    • 这种情况下，上面部分是不存在的。所有新生后缀都没有在原串中的对应子串。

    • 所以所有新生后缀构成同一个等价类，只在尾部出现一次，连一条向根节点（\(1\)）的后缀链接。

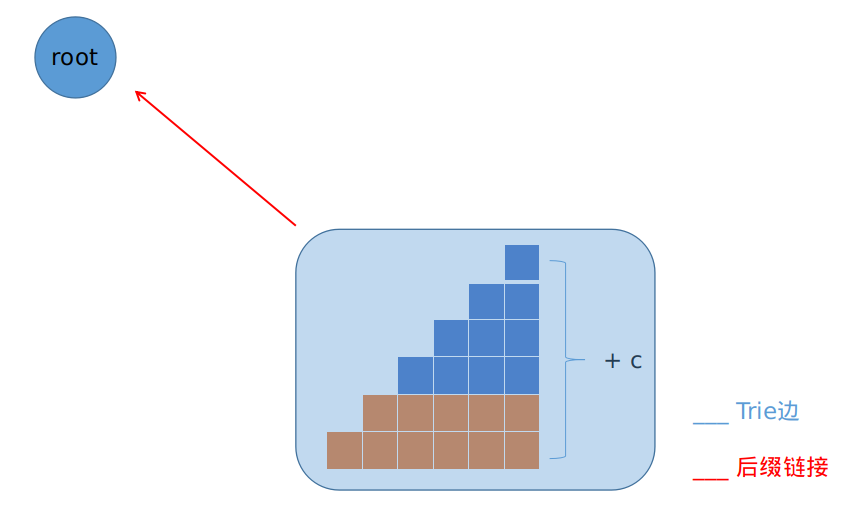
if (p == 0) {
    fa[q] = 1; //莫得其他已有后缀
}

  1. 如果有的话：

设这个点为\(x\)。可能产生的情况有：

$$len[x] = len[p]+1$$

对应下面这样的情况：

这个时候情况比较简单。\(p\)后缀链接上的所有祖先，其\(Trie\)边也都指向这个点\(x\)。我们需要做的，就是把新产生的，原串中未出现的后缀，也就是前面图中的下半部分接上去，完善其后缀链接的信息。

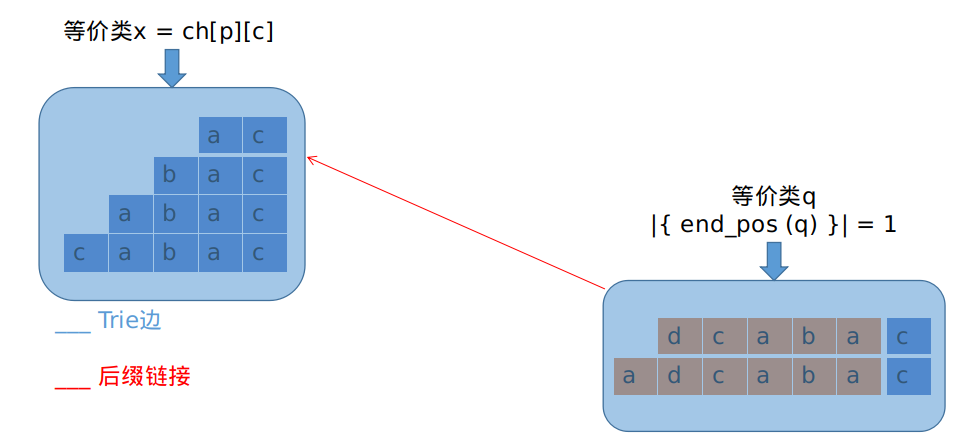
为什么这么接？因为\(x\)是等价类\(q\)字符串长度最相近的等价类嘛～那么底下那部分的事就算完了。

int x = ch[p][c];
if (len[p] + 1 == len[x]) {
    fa[q] = x; //x是q的后缀
}

另一种情况则是这样的：

$$len[x] >len[p]+1$$

也就是说：第一个跳到的，后面接上\(c\)产生的字符串，在原串中出现过的那个等价类（\(p\)），其接上\(c\)之后对应的那个等价类中，存在比当前这个等价类最长的字符串接上\(c\)还要长的串。显然长出来的部分不会再和最开始图中的下半部分吻合，如果吻合自然不被堆在底下。

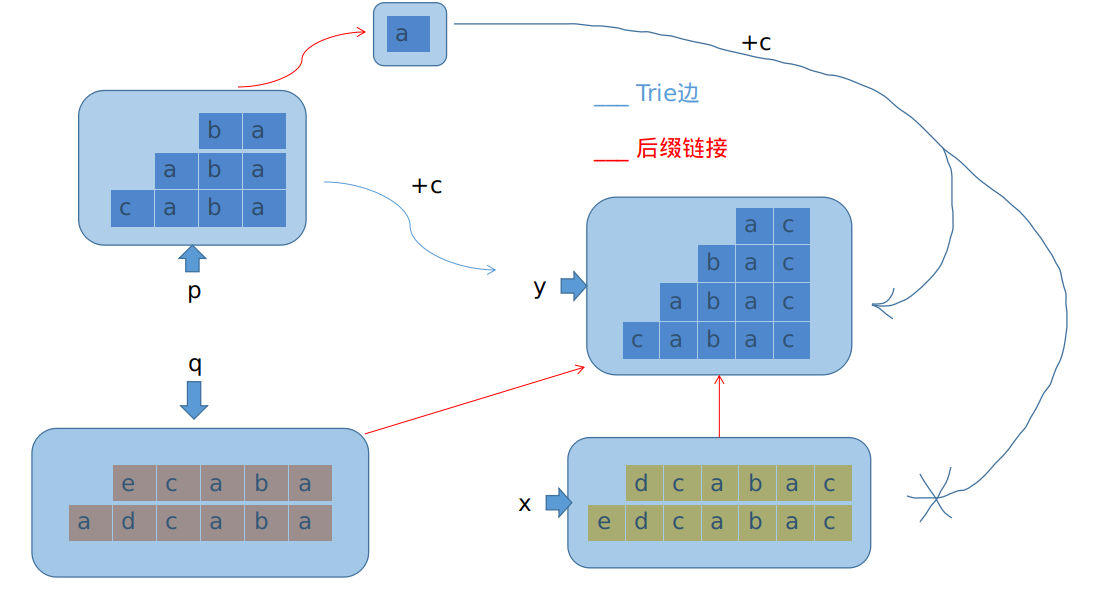
也就是说，这种情况大概长这样：

其中，蓝色部分的\(end\_pos\)会扩大一个，原因是在新串在结尾处再次出现了这些串。但黄色那一部分却并没有作为后缀在新串结尾处再次出现。

连\(end\_pos\)都不一样，那显然就不是同一个等价类了。结论只有一个：分家，把\(x\)分成\(x\)和新节点\(y\)两部分。

来考虑新节点的连边情况。向后连\(Trie\)边等效于再在后面加字符。因为\(c\)已经是结尾处的字符了，所以再添加字符在\(c\)后面的话，结尾处自然不可能匹配得上，字符\(c\)就无法对\(end\_pos\)集合起到任何作用了。也就是说，\(x\)和\(y\)的\(Trie\)边是一致的，做一次\(memcpy\)即可。

int y = ++node;
memcpy (ch[y], ch[x], sizeof (ch[x]));

我们把分出来的\(y\)设置为\(len<=len(p) + 1\)的部分，这样\(p\)在添加字符\(c\)之后就可以正常连接到\(y\)上了。由于\(x\)和\(y\)在原本长度连续的字符串集合中区间的某一长度点断开，所以可以得到\(min\_len(x) = max\_len(y)+1\)，\(y\)是\(x\)在后缀链接上的父亲。同样的，\(y\)在后缀连接上的父亲，应该把原来\(x\)在后缀连接上的父亲继承过来，可以类比于链表的那种插入方式。（注意处理时候的先后）

别忘了把\(q\)也拉过来一条向\(x\)的后缀链接，\(q\)在后缀链接上的父亲也是对应着\(x\)呢。（参考之前的图。）

len[y] = len[p] + 1;
fa[y] = fa[x];
fa[x] = fa[q] = y;

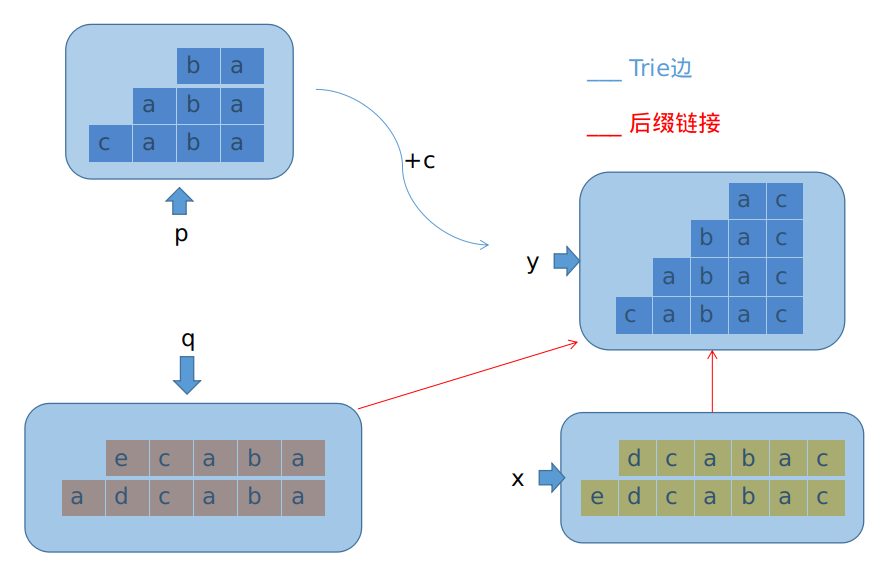
大概就是这样的一个处理方式。（\(Trie\)边实在没法画了\(QwQ\)）

那么\(p\)的祖先的后缀链接呢？节点\(p\)在后缀链接上的所有祖先都还接在\(x\)上呢啊\(QwQ\)

节点\(p\)在后缀链接上的祖先一定是\(p\)对应等价类的后缀，即长度小于\(min\_len(p)\)。也就是说，它们在添加字符\(c\)后，同样应该连接在点\(x\)上。我们把\(p\)点的祖先的连边做一下更新，让它们本来连到\(x\)上的边重定向到\(y\)上。

while (p != 0 && ch[p][c] == x) {
    ch[p][c] = y;
    p = fa[p];
}

完整代码如下：

void Extend (int c) {
	int p = lst, q = ++node; lst = q;
	len[q] = len[p] + 1; siz[q] = 1;
	while (!ch[p][c] && p != 0) {
		ch[p][c] = q;
		p = fa[p];//更新原串后缀的连边
	}
	if (p == 0) {
		fa[q] = 1; //q莫得其他已有后缀
	} else {
		int x = ch[p][c];
		if (len[p] + 1 == len[x]) {
			fa[q] = x; //x成为q的后缀
		} else {
			int y = ++node;
			fa[y] = fa[x];
			fa[x] = fa[q] = y;
			len[y] = len[p] + 1;
			memcpy (ch[y], ch[x], sizeof (ch[x]));
			while (p != 0 && ch[p][c] == x) {
				ch[p][c] = y;
				p = fa[p];
			}
		}
	}
}

作图很辛苦。如果对你有帮助，请记得点一下推荐哦\(QwQ\)

posted @ 2019-02-27 23:38  maomao9173  阅读(1405)  评论(8)  编辑  收藏  举报