数据结构基础

一，数据结构的重要性

 

非常重要

二，数据结构的定义

我们如何把现实中大量而且非常复杂的问题以特定的数据类型(个体)和特定的存储结构(个体的关系)保存到相应的主存储器(内存)中，

以及在此基础上为实现某个功能而执行的相应操作，这个相应的操作也叫做算法

 

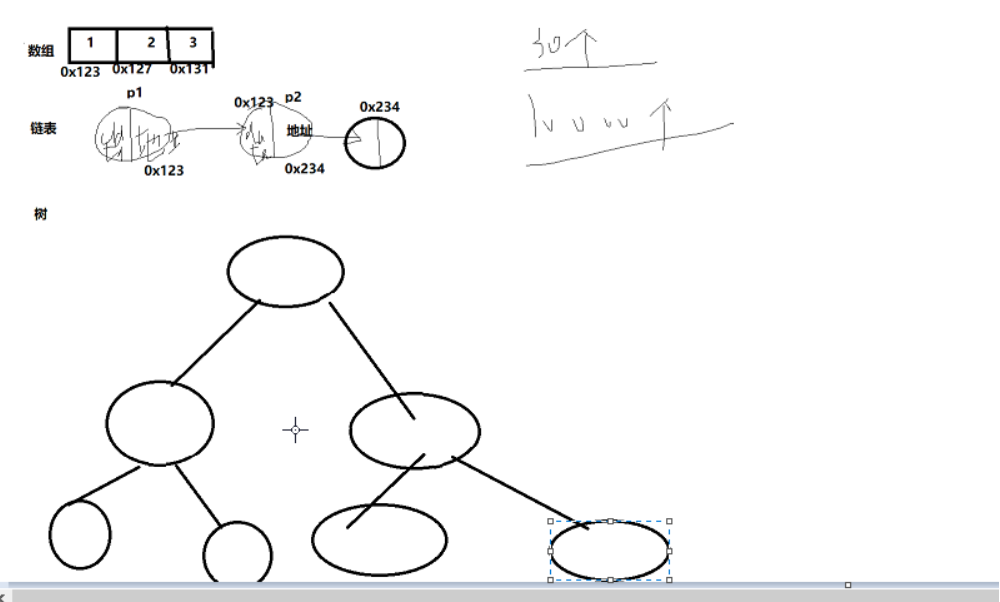
数据结构 == 个体 + 个体的关系
算法 == 对存储数据的操作

 

三，算法

衡量算法的标准
时间复杂度 指的是大概程序执行的次数，而非程序执行的时间
空间复杂度 指的是程序执行过程中，大概所占有的最大内存
难易程度：好的算法打破别人没有的
健壮性：不是合法的报异常，

 

 

总结

 

代码：

空间复杂度


1，排序算法
列表排序

冒泡排序
1，一次冒泡完总会得到一次结果，第二次就次大，直到排完
2、代码关键点：
• 趟数：n-1趟
• 无序区

代码：

def bubble_sort(li):
for i in range(len(li)-1):
for j in range(len(li)-i-1):
if li[j] > li[j+1]:
li[j], li[j+1] = li[j+1], li[j]

startTime = time()

bubbleSort(li)

costTime = time() - startTime
print("bubbleSort : " , costTime)

• 时间复杂度：O(n2)

选择排序

小的放前面

代码：

时间复杂度：O(n2)
#### 选择排序
'''
32, 29, 14, 37, 20
29,32,14,37,20
'''
def selectSort(li):

for i in range(len(li) - 1): #i表示趟数，也表示无序区开始的位置
min = i # 当min等于最小值时
for j in range(i+1, len(li)): #i ， i+1 就是最后一个位置的范围
if li[min] > li[j]: # 两个位置进行比较，如果后面一个比最小小，证明找到最小的
li[min], li[j] = li[j], li[min] # 两个值进行互相交换
# li = [32, 29, 14, 37, 20]
#
# quickSort(li,0,4)
# print(li)

插入排序

代码:

#### 插入排序
def insertSort(li):

for i in range(len(li) - 1): # 表示无序区的第一个数
tmp = li[i] # 摸到的牌
j = i - 1 # 指向有系区最后一个位置

while j >= 0 and li[j] > tmp: # 循环终止条件
li[j+1] = li[j] # 向后移动
j = j - 1
li[j+1] = tmp

快速排序

 

代码

快速排序的时间复杂度O(nlogn)
#### 快速排序

from timeit import Timer
from random import shuffle
from time import time

def partition(li, left, right):
tmp = li[left] #先把5取出来
while left < right:

while left < right and li[right] > tmp: #如果降序排列修改li[right] <= tmp
right = right - 1 #从右边找比5小的数，填充到5的位置
li[left] = li[right]

while left < right and li[left] < tmp: #如果降序排列修改li[right] >= tmp
left = left + 1 # 从左边找比5大的数字放在右边的空位
li[right] = li[left]

li[left] = tmp #当跳出循环条件的时候说明找到了，并且把拿出来的5在放进去

return left

def quickSort(li, left, right):
'''快速排序的两个关键点：归位，递归'''
if left < right: #至少有两个元素，才能进行递归
mid = partition(li, left, right)#找到归位的位置
quickSort(li, left, mid - 1)#递归，右边的-1
quickSort(li, mid+1, right)#递归，左边的+1

startTime = time()

quickSort(li, 0, len(li)-1)

costTime = time() - startTime
print("quickSort : " , costTime)

 

2，查找算法
列表：
将无序列表变为有序列表

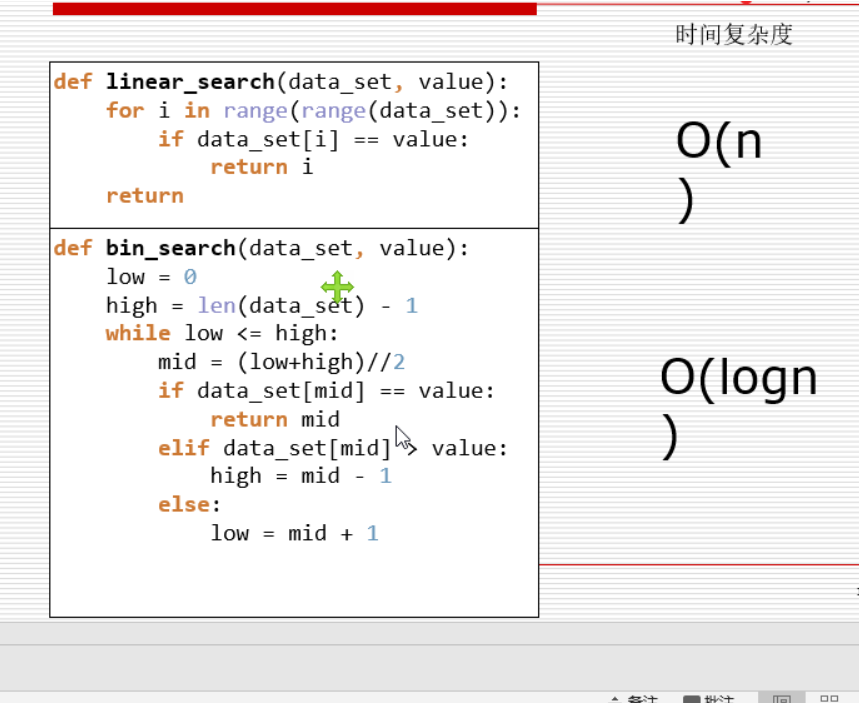
二分法
def serach(li,val):
low = 0 #开始索引
high = len(li) - 1 #结束索引
while low<=high:
mid = (low+high)//2
if li[mid] > val: #如果中间值比传进来的值大就从中间值的左边找
high = mid-1
elif li[mid]<val:
low = mid +1
else:
return mid
else:
return -1
li = list(range(0,101,2))
print(serach(li,98))
# ==================递归版的二分查找===========
def bin_serach_rec(li,val,low,high):
if low<=high:
mid = (low+high)//2
if li[mid] >val:
return bin_serach_rec(li,val,low,mid-1,)
elif li[mid]<val:
return bin_serach_rec(li,val,mid+1,high)
else:
return mid
else:
return
li = list(range(0,101,2))
print(serach(li,98))

 

四，线性结构
1，连续存储
数组
□ 优点:
® 存取速度快
□ 缺点：
® 事先需要知道数组的长度
® 需要大块的连续内存
® 插入删除非常的慢，效率极低

2，离散存储

 

链表

 

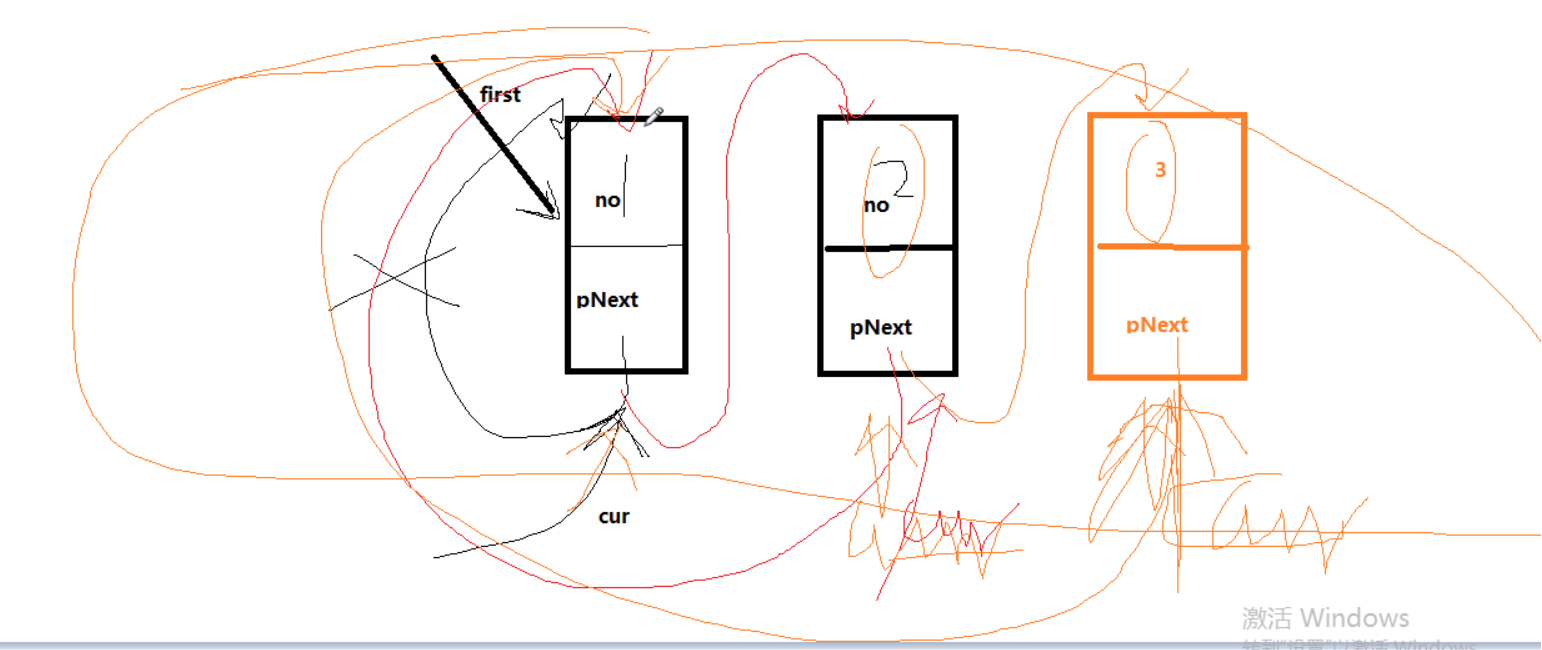
单链表 伪代码

 

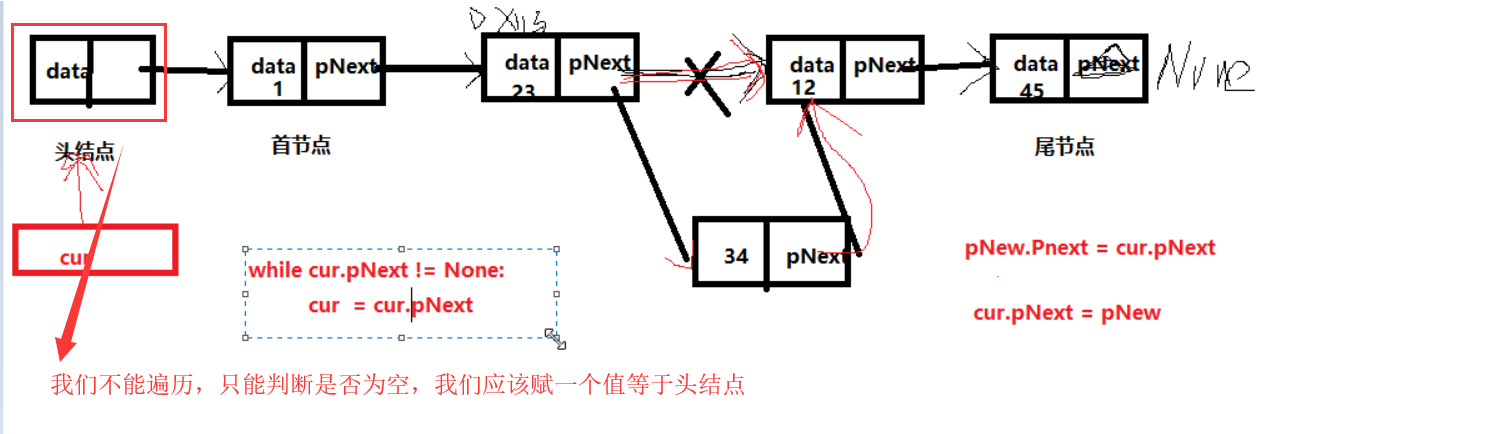
英雄排行榜代码：

    class Hero(object):
        def __init__(self, no=None, nickname=None, name=None, pNext = None):
            self.no = no
            self.nickname = nickname
            self.name = name
            self.pNext = pNext
    
    #### 添加节点
    def addHero(head, pNew):
        cur = head
        # while cur.pNext != None:
        #     cur = cur.pNext
        #
        # cur.pNext = pNew
    
        while cur.pNext != None:
            if cur.pNext.no > pNew.no:
                break
    
            cur = cur.pNext
    
        pNew.pNext = cur.pNext
        cur.pNext = pNew
    
        
    #### 遍历节点
    def showHero(head):
        if isEmpty(head):
            return None
    
        cur = head
    
        while cur.pNext != None:
            print("英雄的编号是: %s, 外号是：%s, 姓名:%s" % (cur.pNext.no, cur.pNext.nickname, cur.pNext.name))
            cur = cur.pNext
    ### 判断是否为空
    def isEmpty(head):
        if head.pNext != None:
            return False
        return True
    
    ## 删除节点
    def delHero(head, no):
        cur = head
        while cur.pNext != None:
            if cur.pNext.no == no:
                # 开始删除
                cur.pNext = cur.pNext.pNext
                break
            cur = cur.pNext
        else:
            print('没有找到')
    
    ### 链表的长度
    def getLength(head):
        length = 0
        cur = head
        while cur.pNext != None:
            cur = cur.pNext
            length = length + 1
    
        return length
    
    
    
    
    # 头结点
    head = Hero()
    
    ## 首节点
    h1 = Hero(1, '及时雨', '宋江')
    h2 = Hero(2, '玉麒麟', '卢俊义')
    h3 = Hero(6, '豹子头', '林冲')
    h4 = Hero(4, '入云龙', '公孙胜')
    h5 = Hero(5, '入云龙', '公孙胜')
    
    addHero(head, h1)
    addHero(head, h2)
    addHero(head, h3)
    addHero(head, h4)
    addHero(head, h5)
    
    showHero(head)
    print(getLength(head))
    

 

双链表

 

        class Node(object):
            def __init__(self, data=None):
                self.data = data
                self.next = None
                self.prior = None
        双向链表的操作：
        
        插入：
        
        p.next = curNode.next
        curNode.next.prior = p
        curNode.next = p
        p.prior = curNode
        删除：
        
        p = curNode.next
        curNode.next = p.next
        p.next.prior = curNode
        del p

 

环形列表

 

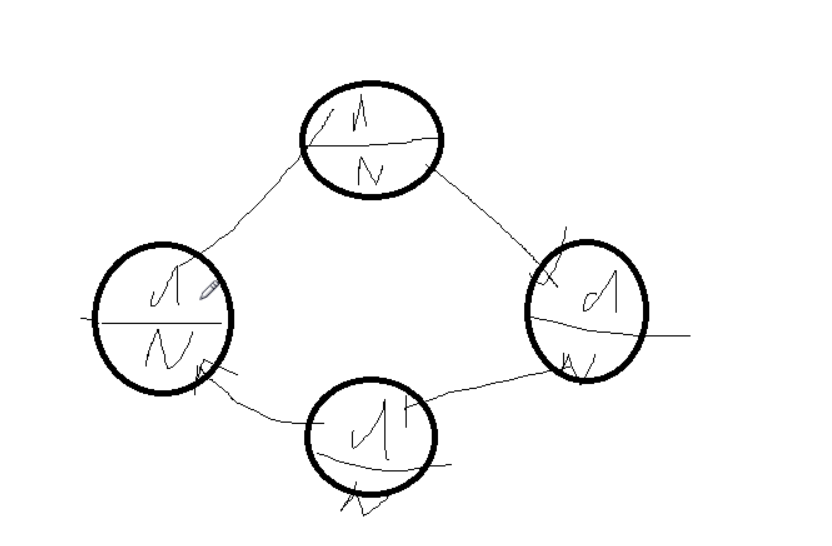
3，约瑟夫问题
设编号为1，2，… n的n个人围坐一圈，约定编号为k（1<=k<=n）的人从1开始报数，数到m 的那个人出列，它的下一位又从1开始报数，数到m的那个人又出列，依次类推，直到所有人出列为止，由此产生一个出队编号的序列

 

递归
队列
栈

 

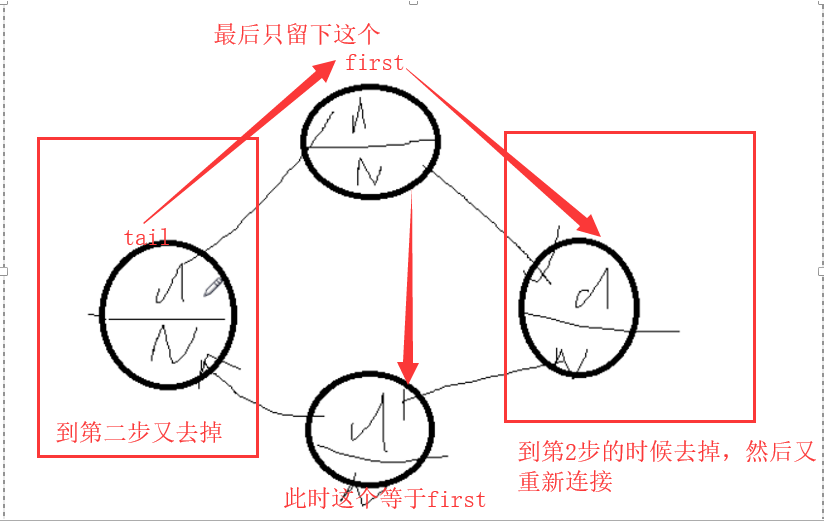
代码：

    class Child(object):
        first =  None
        def __init__(self,no= None,pNext=None):
            self.no=no
            self.pNext=pNext
        def add(self):
            cur = None
            for i in range(4):
                child=Child(i+1)
    
                if i == 0:
                    self.first = child  # 第一个孩子
                    child.pNext = self.first   # 值向下一个
                    cur = self.first           # 创建
                else:
                    cur.pNext = child
                    child.pNext = self.first
                    cur = cur.pNext
        def show(self):
            cur = self.first
            while cur.pNext != self.first:
                print("当前孩子的编号：%s"%cur.no)
                cur = cur.pNext
            print("当前孩子的编号是：%s "%cur.no)
    
        def countChild(self, m, k):
            tail = self.first
    
            while tail.pNext != self.first:
                tail = tail.pNext
    
            #### 当退出循环的时候，tail已经是在first的后面了
    
            for i in range(k - 1):
                tail = tail.pNext
                self.first = self.first.pNext
    
            while tail != self.first:
                for i in range(1):
                    tail = tail.pNext
                    self.first = self.first.pNext
    
                self.first = self.first.pNext
                tail.pNext = self.first
    
            print("最终剩下的孩子的编号是: %s" % self.first.no)
    
    c = Child()
    c.addChild(1000)
    c.showChild()
    c.countChild(3, 2)