MATLAB入门实验-MATLAB实验1...MATLAB实验8
MATLAB入门实验-MATLAB实验1...MATLAB实验8
实验1 MATLAB系统环境运算基础
一、实验目的
- 掌握启动和退出MATLAB的方法。
- 掌握MATLAB操作界面的组成。
- 掌握建立矩阵的方法。
- 掌握MATLAB表达式的书写规则以及常用函数的使用方法。
二、实验内容
1、启动MATLAB系统环境,完成下列操作。
在MATLAB命令行窗口输入以下命令后,观察工作区窗口的内容。
3、先建立自己的工作文件夹,再将自己的工作文件夹设置MATLAB工作空间的使用情况并保存全部变量。
(1)\(Z_{1} = \frac{2*sin85^{\circ}}{1+e^{2}}\)
Z1 = 2*sind(85)/(1+exp(2))
| 运行结果 |
|---|
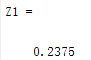 |
(2)\(Z_{2} = \frac{\pi }{x+y}\),其中\(x=12,y=10^{-5}\)。
x=12;y= 10^-5;
Z2 = pi/(x+y)
| 运行结果 |
|---|
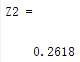 |
(3)\(Z_{3}= \frac{1}{2} \ln_{}{x+\sqrt{1+x^{2}}}\) ,其中\(x=\begin{bmatrix} 2& 1+2i\\ -0.45&5\end{bmatrix}\)。
x = [2 1+2i;-0.45 5];
Z3 = 1/2*log(x+sqrt(1+x^2))
| 运行结果 |
|---|
 |
(4)\(Z_{4}=\frac{e^{0.3 a}-e^{-0.3 a}}{2} \sin (a+0.3)+\ln \frac{0.3+a}{2}\) , 当 a 取 -3.0,-2.9,-2.8, ……, 2.8,2.9,3.0 时, 求各点的函数值。
a=-3:0.01:3;
Z4 = (exp(0.3.*a)-exp(-0.3.*a))/2.*sin(a+0.3)...
+log((0.3+a)/2)
| 运行结果 |
|---|
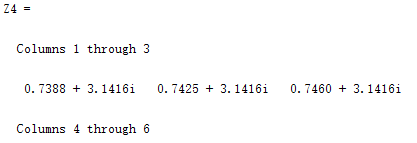 |
4、已知 \(A=\left[\begin{array}{ccc}12 & 34 & -4 \\34 & 7 & 87 \\3 & 65 & 7\end{array}\right]\),\(B=\left[\begin{array}{ccc}1 & 3 & -1 \\2 & 0 & 3 \\3 & -2 & 7\end{array}\right]\),
求下列表达式的值。
(1) \(A^{\wedge} 3\) 和 \(A .^{\wedge} 3\)
(2) \(A^{*} B\) , \(B^{*} A\) ,与 \(A .^{*}B\)
(3) \(A / B\) 及 \(B \backslash A\)
(4) \([\mathrm{A}, \mathrm{B}]\) 和 \(\left[\mathrm{A}([1,3],:) ; \mathrm{B}^{\wedge} 2\right]\)
A=[12 34 -4;34 7 87;3 65 7;];B=[1 3 -1;2 0 3;3 -2 7];
%(1)
A*B,B*A,A.*B
%(2)
A^3,A.^3
%(3)
A/B,B\A
%(4)
[A,B],[A([1,3],:);B^2]
| 运行结果 |
|---|
%(1)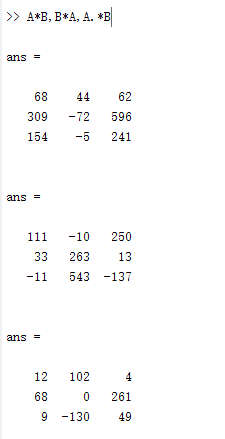 |
%(2) |
%(3) |
%(4) |
5、设有矩阵 A 和 B
(1) 求它们的乘积 \(\mathrm{C}=\mathrm{A} * \mathrm{~B}\) .
(2) 将矩阵 \(\mathrm{C}\) 的右下角 3 * 2 子矩阵赋给 \(\mathrm{D}\) .
A=(reshape(1:1:25,5,5))';
B=[3 0 16;17 -6 9;0 23 -4;9 7 0;4 13 11];
%(1)
C=A*B
%(2)
D = C(3:5,2:3)
| 运行结果 |
|---|
%(1)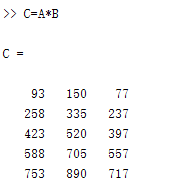 |
%(2) |
6、完成以下操作。
(1) 求[100,999]之间能被21整除的数的个数。
A = [100:1:999];
B = find(rem(A,21)==0);
length(B)
| 运行结果 |
|---|
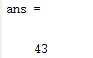 |
(2) 建立一个字符串向量,删除其中大写字母。
E='aadfW4DF4';
F=find(E>='A'&E<='Z');%find返回下标索引
E(F)=[]
| 运行结果 |
|---|
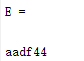 |
实验2 MATLAB矩阵处理
一、实验目的
- 掌握生成特殊矩阵的方法。
- 掌握矩阵处理的方法。
- 掌握用矩阵求逆法解线性方程组的方法。
二、实验内容
1、设有分块矩阵 \(\mathrm{A}=\left[\begin{array}{ll}E_{3 * 3} & R_{3 * 2} \\O_{2 * 3} & S_{2 * 2}\end{array}\right]\),其中 \(\mathrm{E}\)、\(\mathrm{R}\)、\(\mathrm{O}\)、\(\mathrm{S}\) 分别为单位矩阵、随机矩阵、零矩阵和对角阵,试通过数值计算验证 \(\left[A^{2}\right]=\left[\begin{array}{cc}E & R+R S \\O & S^{2}\end{array}\right]\) 。
E = eye(3,3);R = rand(3,2);O = zeros(2,3);S = diag([1,2]);
A = [E R;O S];
Z1 = A^2;
Z2 = [E R+R*S; O S^2];
Z1-Z2
| 运行结果 |
|---|
 |
2、建立一个5*5矩阵,求它的行列式值、迹、秩和范数。
E = rand(5);%5阶(0.1)随机方阵
A = det(E)%行列式的值
B = trace(E)%矩阵的迹
C = rank(E)%矩阵的秩
D1 = norm(E,1) %矩阵E的1-范数
D2 = norm(E) %矩阵E的2-范数
D3 = norm(E,inf) %矩阵E的∞-范数
| 运行结果 |
|---|
 |
4、已知\(\mathrm{A}=\left[\begin{array}{ccc}-29 & 6 & 18 \\20 & 5 & 12 \\-8 & 8 & 5\end{array}\right]\),求 \(\mathrm{A}\) 的特征值及特征向量,并分析其数学意义。
A=[-29 6 18;20 5 12;-8 8 5];
[X,D] = eig(A)
%矩阵A的全部特征值构成对角阵D,相应的特征向量构成矩阵X
| 运行结果 |
|---|
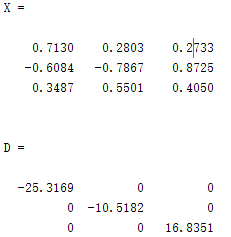 |
| \(A\)的特征值\(D\)及特征向量\(X\),分析其数学意义——有满足:\(A=XDX^{-1}\) |
5、下面是一个线性病态方程组:\(\left[\begin{array}{lll}1 / 2 & 1 / 3 & 1 / 4 \\1 / 3 & 1 / 4 & 1 / 5 \\1 / 4 & 1 / 5 & 1 / 6\end{array}\right]\left[\begin{array}{l}x_{1} \\x_{2} \\x_{3}\end{array}\right]=\left[\begin{array}{l}0.95 \\0.67 \\0.52\end{array}\right]\)
(1)用矩阵求逆法求方程的解。
(2)将方程右边向量元素 \(b_3\) 改为0.53,再求解,并比较 \(b_3\) 变化和解的相对变化。
(3)计算系数矩阵 \(A\) 的条件数并分析结论。
A = [1/2 1/3 1/4;1/3 1/4 1/5;1/4 1/5 1/6];
b = [0.95 0.67 0.52]';
%(1)矩阵求逆法求方程的解
x1 = inv(A)*b
%(2)
b = [0.95 0.67 0.53]';%b_3改为0.53,再求解
x2 = inv(A)*b
%(3)
A = [1/2 1/3 1/4;1/3 1/4 1/5;1/4 1/5 1/6];
C1 = cond(A,1) %矩阵A的1-范数下的条件数
C2 = cond(A) %矩阵A的2-范数下的条件数
C3 = cond(A,inf) %矩阵A的∞-范数下的条件数
| 运行结果 |
|---|
 |
| (2) \(b_3\) 从0.52变大为0.53,相应解,\(x^1,x^3\)都变大、\(x^2\)变小。 |
| (3)系数矩阵\(A\)的条件数都不接近1,矩阵的系能差。 |
实验3 顺序结构程序设计
一、实验目的
- 掌握建立和执行M文件的方法。
- 掌握输入输出的方法。
- 握顺序结构程序设计方法。
二、实验内容
1、从键盘输入一个4位整数,按如下规则加密后输出。
加密规则:每位数字都加上7,然后用和除以10的余数取代该数字;然后将第一位数与第三位数互换,第二位数与第四位数互换。
x=ones(1,4);
x(1)=input('输入第一位:');
x(2)=input('输入第二位:');
x(3)=input('输入第三位:');
x(4)=input('输入第四位:');
x=rem(7+x,10);
y=1000.*x(3)+100.*x(4)+10.*x(1)+x(2)
| 运行结果 |
|---|
 |
2、输入一个正的实数 x ,分别输出 x 的整数部分和小数部分。
x=input('输入一个正的实数:');
y1=fix(x)
y2=x-y1
| 运行结果 |
|---|
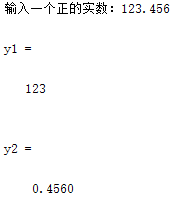 |
4、输入3个整数给a、b、c,然后交换它们的值;把a中原来的值赋给b,把b中原来的值赋给c,把c中原来的值赋给a。
a=input('输入第一个整数:')
b=input('输入第二个整数:')
c=input('输入第三个整数:')
A=[a b c];
b=A(1)
c=A(2)
a=A(3)
| 运行结果 |
|---|
 |
5、随机产生一个3位整数,将它的十位数变为0。例如,如果生成的3位整数为738,则输出为708。
A=randi ([100,999],1,1)
A=fix(A/100)*100+rem(A,10)
| 运行结果 |
|---|
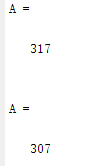 |
实验4 选择结构程序设计
一、实验目的
- 掌握利用 if 语句实现选择结构的方法。
- 掌握利用 switch 语句实现多分支选择结构的方法。
- 掌握 try 语句的使用方法。
二、实验内容
1、求分段函数的值。\(\mathrm{y}=\left\{\begin{array}{lr}x^{2}+x-6, & x<0 \text { 且 } x \neq-3 \\x^{2}-5 x+6, & 0 \leq x<5 \text { 且 } x \neq 2 \text { 及 } x \neq 3\\x^{2}-x-1, & \text { 其他 }\end{array}\right.\)
用 if 语句实现,分别输出 x=-5.0 ,-3.0 ,1.0 ,2.0 ,2.5 ,3.0 ,5.0 时的y值。
x=[-5 -3 1 2 2.5 3 5];
for i=1:7
if and(x(i)<0,x~=-3)
y(i)=x(i)^2+x(i)-6;
elseif x(i)>=0 & x(i)<5 & x(i)~=2 & x(i)~=3
y(i)=x(i)^2-5*x(i)+6;
else
y(i)=x(i)*2-x(i)-1;
end
end
disp(y);
| 运行结果 |
|---|
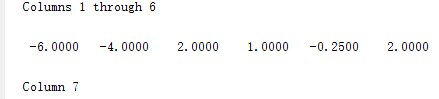 |
2、输入一个百分制成绩,要求输出成绩等级A、B、C、D、E。其中90~100分为A,80~89分别为B,70~79分别为C,60~69分别为D,60分以下为E。
要求:
(1) 分别用if语句和switch语句实现。
(2) 输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
%2.1
a=input('输入一个百分制成绩:','s');
%input()存数字或矩阵
%input('','s')存字符串
k=str2double(a);
x=floor(k/10);
%附:fix(),向零方向取整。发现输入-4,取整为0,不报错
%附:floor(),不大于自变量的最大整数
%附:ceil(),不小于自变量的最大整数
%附:rount(),四舍五入到最临近的整数
%str2double()把字符转换为数字。是“数字”则正常转换、不是则得NaN
%isnan()判断是否为NaN
if isnan(k)
y='error!';
else
if or(x==10,x==9)
y='A';
elseif x==8
y='B';
elseif x==7
y='C';
elseif x==6
y='D';
elseif x==6|x==5|x==4|x==3|x==2|x==1|x==0
y='E';
else
y='error!';
end
end
disp(y);
% 2.2
a=input('输入一个百分制成绩:','s');
k=str2double(a);
x=floor(k/10);
if isnan(k)
y='error!';
else
switch x
case 10
case 90
y='A';
break;
case 8
y='B';
break;
case 7
y='C';
break;
case 6
y='D';
break;
case 6
case 5
case 4
case 3
case 2
case 1
case 0
y='E';
break;
otherwise
y='error!';
end
end
disp(y);
| 运行结果 |
|---|
  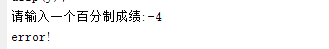    |
4、设计程序,完成两位数的加、减、乘、除四则运算,即产生两个两位随机整数,再输入一个运算符号,完成对应的运算,并显示相应的结果。
x=rand(1,2);
y=input('输入一个运算符号:','s');
switch y
case '+'
z=x(1)+x(2);
break;
case '-'
z=x(1)-x(2);
break;
case '*'
z=x(1)*x(2);
break;
case '/'
z=x(1)/x(2);
break;
otherwise
z='error!';
end
disp(z);
| 运行结果 |
|---|
 |
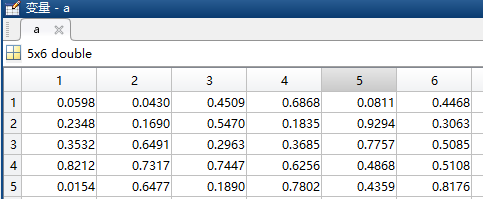
5、建立5*6矩阵,要求输入矩阵第n行元素。当n值超过矩阵的行数时,自动转为输出矩阵最后一行元素,并给出错误信息。
a=rand(5,6);
x=input('输入矩阵第n行:\n');
m=size(a,1);%求矩阵行数
%n=size(a,2);%求矩阵列数
%[m,n]=size(a);%求矩阵行列数
if ~(x<=m)
disp('错误!超过矩阵的行数,转为自动输出矩阵最后一行');
x=m
end
y=a(x,:);
disp(y);
| 运行结果 |
|---|
  |
实验5 循环结构程序设计
一、实验目的
- 掌握利用for语句实现循环结构的方法。
- 掌握利用while语句实现循环结构的方法。
- 熟悉利用向量运算来代替循环操作的方法。
二、实验内容
1、已知\(y=\frac{1}{3}+\frac{1}{3} \cdot \frac{1}{3^{3}}+\frac{1}{5} \cdot \frac{1}{5^{3}}+\cdots+\frac{1}{2 n-1} \cdot \frac{1}{3^{2 n-1}}\left(=\frac{\ln 2}{2}\right)\);求y的近试值。当n分别取100、1000、10000时,结果是多少?分别使用循环结构和向量运算。
%1.1
R=[];%循环结构
for n=[100,1000,10000];
s=0;
for i=1:n
s=s+1/(2*i-1) * 1/(3^(2*i-1));
end
R=[R,s];
end
R
%1.2
R=[];%向量运算
for n=[100,1000,10000];
i=1:n; %生成1到n的行向量
%s=sum(1./i);
s=sum(1./(2.*i-1) .* 1./(3.^(2.*i-1)));
R=[R,s];
end
R
| 运行结果 |
|---|
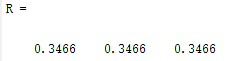 |
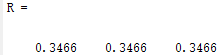 |
根据\(y=1+\frac{1}{3}+\frac{1}{5}+\cdots+\frac{1}{2 n-1}\),求:
(1) y ❤️ 时的最大 n 值。
(2) 与(1)的 n 值对应的 y 值。
n=0;
y=0;
while y<3
n=n+1;
y=y+n;
end
disp(['n=',num2str(n),',y=',num2str(y)]);
%n,y本是double型数据。class(n)查看
%disp(['n=',n,',y=',y])错误!
%disp([n,y]);
| 运行结果 |
|---|
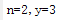 |
4、已知 \(\left\{\begin{array}{c}f_{1=1} \\f_{2}=0 \\f_{3}=1 \\f_{n}=f_{n-1}-2 f_{n-2}+f_{n-3} \quad(n>3)\end{array}\right.\),求f1~f100中:
(1) 最大值、最小值、各数之和。
(2) 正数、零、负数的个数。
f(1)=1;f(2)=0;f(3)=1;
format long g%对双精度,显示15位定点或浮点格式;对单精度,显示7位
n=input('输入一个n:');
for i=4:n
f(i)=f(i-1)-2*f(i-2)+f(i-3);
end
%(1)
max=max(f)
min=min(f)
sum=sum(f)
%(2)
postive=length(f(f>0))
negative=length(f(f<0))
zero=length(f(f==0))
| 运行结果 |
|---|
 |
5、若两个连续自然数的乘积减1是素数,则称这两个连续自然数的亲密数对,该素数是亲密素数。例如,2×3-1=5,由于5是素数,所以2和3是亲密数对,5是亲密素数。求[2,50]区间内:
(1) 亲密数对的对数。
(2) 与上述亲密数对对应的所以亲密素数之和。
a=2:50;
count=0;
sum=0;
for i = a
if i==49
break;
end
x(i)=a(i)*a(i+1)-1;
if isprime(x(i))%isprime判断是否为素数
count=count+1;
sum=sum+x(i);
end
end
disp(['[2,50]区间亲密数对的对数',num2str(count)]);
disp(['所有亲密素数之和',num2str(sum)]);
| 运行结果 |
|---|
 |
实验6 函数文件
一、实验目的
- 理解函数文件的概念。
- 掌握定义和调用MATLAB函数的方法。
二、实验内容
1、定义一个函数文件,求给定复数的指数、对数正弦和余弦,并在脚本文件中调用该函数文件。
%函数文件 f61.m
function [ expval,logval,sinval,cosval ] = f61( inputArg1 )
expval=exp(inputArg1);
logval=log(inputArg1);
sinval=sin(inputArg1);
cosval=cos(inputArg1);
end%
x=input('输入x:')
[ expval,logval,sinval,cosval ]=f61(x)
| 运行结果 |
|---|
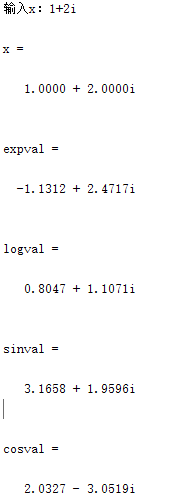 |
2、某物理系统可用下列方程组来表示:
从键盘输入\(m^{1}\)、\(m^{2}\)和θ的值,求 \(a^{1}\)、\(a^{2}\)、\(N^{1}\) 和 \(N^{2}\) 的值。其中 \(g\) 取9.8,输入 \(θ\) 时以角度为单位。
%函数文件 f62.m
function [ value ] = f62( m1,m2,ag )
g=9.8;
P=[m1*cos(ag),-m1,-sin(ag),0;m1*sin(ag),0,-cos(ag),0;...
0,m2,-sin(ag),0;0,0,-cos(ag),1;]
q=[0,m1*g,0,m2*g]';
value=inv(P)*q;
end
m1=input('输入m1:');
m2=input('输入m2:');
ag=input('输入角度:');
[result]=f62(m1,m2,ag)
| 运行结果 |
|---|
 |
5、已知 \(y=\frac{f(40)}{f(30)+f(20)}\)
(1) 当 \(\mathrm{f}(\mathrm{n})=\mathrm{n}+10 \ln \left(n^{2}+5\right)\) 时, \(y\) 的值是多少?
(2) 当 \(f(n)=1 \times 2+2 \times 3+3 \times 4+\cdots+n \times(n+1)\) 时,\(y\) 的值是多少?
%函数文件f651.m
%(1)
function m=f651(n)
m=n+10*log(n*n+5);
end
%函数文件f652.m
%(2)
function m=f652(n)
m=0;
for i=1:n
m=n*(n+1)+m;
end
end
y=f651(40)/(f651(30)+f651(20))
y=f652(40)/(f652(30)+f652(20))
| 运行结果 |
|---|
 |
 |
实验7 绘图操作
一、实验目的
- 掌握绘制二维图形的方法。
- 掌握绘制三维图形的方法。
- 掌握绘制图形的辅助操作。
二、实验内容
1、绘制函数曲线。
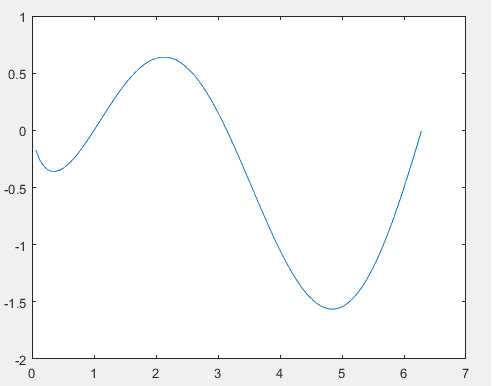
(1) 设 \(\mathrm{y}=\left(0.5+\frac{3 \sin x}{1+x^{2}}\right) \cos x\),把 \(\mathrm{x}=0 \sim 2 \pi\) 区间分为101点,绘制函数的曲线。
x=linspace(0,2*pi,101)
y=log(x).*sin(x);
plot(x,y)
(2) 已知 \(\mathrm{y}=\left\{\begin{array}{c}\frac{x+\sqrt{\pi}}{e^{2}}, \quad x \leq 0 \\ \frac{1}{2} \ln \left(x+\sqrt{1+x^{2}}\right), \quad x>0\end{array}\right.\),在\(-5 \leq \mathrm{x} \leq 5\) 区间绘制函数曲线。
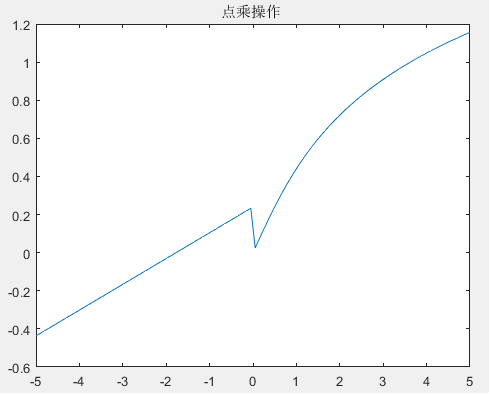
%点乘操作
x=linspace(-5,5,100)
y=(x<=0).*( (x+sqrt(pi))./exp(2) ) + (x>0).*( 1/2*log(x+sqrt(1+x.^2)) )
plot(x,y)
title('点乘操作 ')
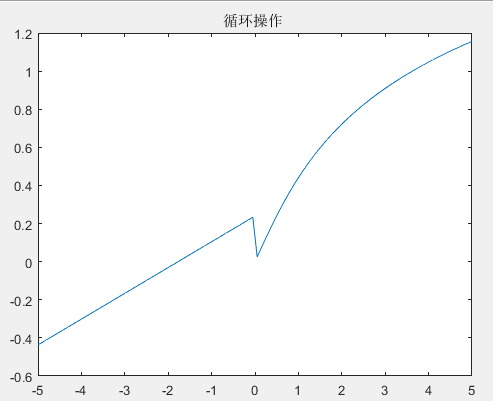
%循环判断操作
x=linspace(-5,5,100)
y=[];
for x0=x
if x0<0
y=[y,(x0+sqrt(pi))/exp(2)];
elseif x0>0
y=[y,1/2*log(x0+sqrt(1+x0^2))];
else y=[y,x0^2];
end
end
plot(x,y)
title('循环操作 ')
(3) 绘制极坐标曲线 \(\rho=10 \sin (1+5 \theta)\)。
t=0:pi/50:20*pi;%弧度
r=10.*sin(1+5*t);
polar(t,r)
| 运行结果 |
|---|
 |
| 运行结果 |
  |
| 运行结果 |
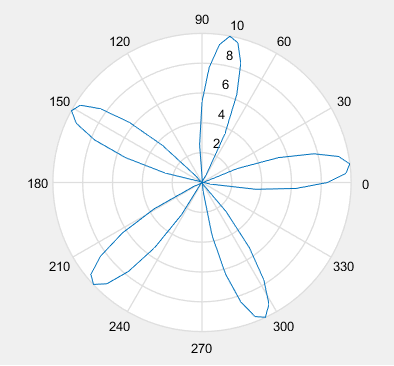 |
2、已知 \(y_{1}=x^{2}, y_{2}=\cos (2 x)\), \(y_{3}=y_{1} * y_{2}\),完成下列操作。
(1) 在同一坐标系下用不同的颜色和线型绘制3条曲线。
x=(0:pi/100:2*pi)';
y1=x.^2;
y2=cos(2*x);
y3=y1.*y2;
plot(x,y1,'k',x,y2,'b--',x,y3,'r:')
(2) 以子图形式绘制3条曲线。
%使用subplot(m,n,p)子图分成m行n列,指定第P幅图;
x=(0:pi/100:2*pi)';
y1=x.^2;
y2=cos(2*x);
y3=y1.*y2;
subplot(2,2,1);
plot(x,y1,'k')
subplot(2,2,2);
plot(x,y2,'b--')
subplot(2,2,3);
plot(x,y3,'r:')
(3) 分别用条形图、阶梯图、杆图和填充图绘制三条曲线。
%bar,stairs,stem,fill(用非白色的颜色进行实心填充,不然看不到现象),参考p118-p122
subplot(2,2,1);
bar(x,y1,'r')
subplot(2,2,2);
stairs(x,y1,'b')
subplot(2,2,3);
plot(x,y1,'y')
subplot(2,2,3);
stem(x,y2,'y')
subplot(2,2,4);
fill(x,y2,'k')
subplot(2,2,1);
bar(x,y,3,'r')
subplot(2,2,2);
stairs(x,y3,'b')
subplot(2,2,4);
fill(x,y,2,'r')
subplot(2,2,1);
bar(x,y,2,'r')
subplot(2,2,2);
stairs(x,y2,'b')
subplot(2,2,3);
stem(x,y3,'y')
subplot(2,2,4);
fill(x,y3,'k')
| 运行结果 |
|---|
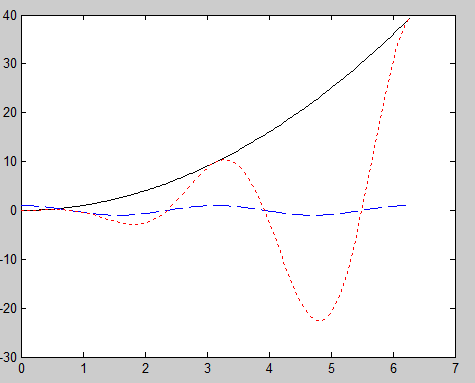 |
| 运行结果 |
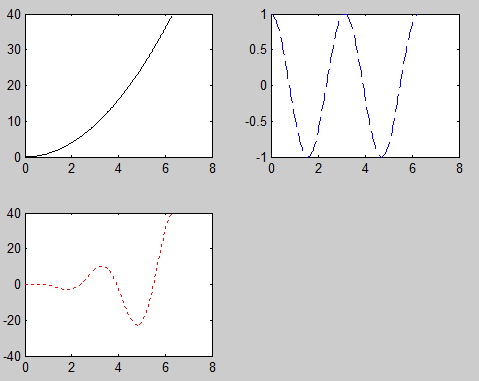 |
| 运行结果 |
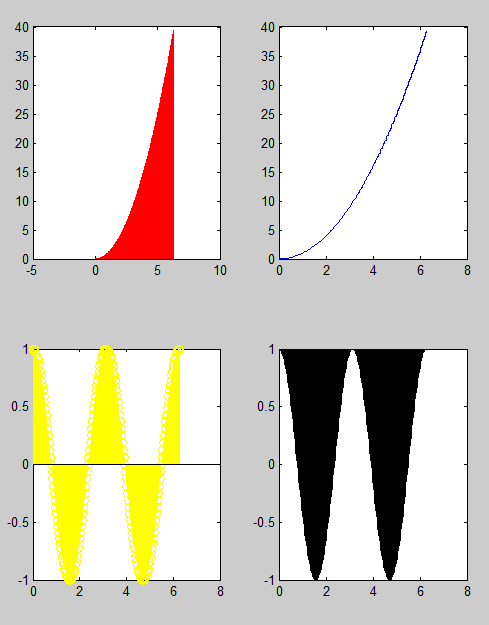 |
实验8 数据分析与多项式计算
一、实验目的
- 掌握数据统计和分析的方法
- 掌握多项式的常用计算。
- 掌握数据插值与曲线拟合的方法及其应用。
二、实验内容
1、利用 MATLAB 提供的 rand 函数生成 30000 个符合均匀分布的随机数,然后检验随机数的性质。
(1) 均值和标准差。
(2) 最大元素和最小元素。
(3) 大于0.5的随机数个数占总数的百分比。
X=rand(30000,1);
%(1)
mean=mean(mean(X))
std=std(std(X))
%(2)
max=max(X)
min=min(X)
%(3)
count=find(X>0.5);
length=length(count);
result=length/30000
| 运行结果 |
|---|
 |
2、将100个学生5门功课的成绩存入矩阵 \(P\) 中,进行如下处理。
(1)分别求每门课的最高分、最低分及相应学生序号。
(2)分别求每门课的分均分和标准差。
(3)5门课的总分的最高分、最低分及相应学生序号。
(4)将5门课总分按从大到小顺序存入 \(score\) 中,相应学生序号存入 \(num\) 。
P=100*rand(100,5);
%(1)
[eachmax,number1]=max(P)
[eachmin,number2]=min(P)
%(2)
eachmean=mean(P)
eachstd=std(P)
%(3)
[hall,number3]=max(sum(P,2))
[lall,number4]=min(sum(P,2))
%(4)
[score0,num0]=sort(sum(P,2),'descend');%按照从大到小
score=reshape(score0,10,10)%方便显示,进行转换
num=reshape(num0,10,10)
| 运行结果 |
|---|
 |
 |
 |
3、有3个多项式\(P_{1}(x)=x^{4}+2 x^{3}+4 x^{2}+5, P_{2}(x)=x+2, P_{3}(x)=x^{2}+ 2 x+3\) ,试进行下列操作。
(1) 求 \(P(x)=P_{1}(x)+P_{2}(x)+P_{3}(x)\)
(2) 求 \(P(x)\) 的根。
(3) 当x取矩阵\(A\)的每一元素时,求 \(P(x)\) 的值。其中 \(A=\left[\begin{array}{ccc}-1 & 1.2 & -1.4 \\ 0.75 & 2 & 3.5 \\ 0 & 5 & 2.5\end{array}\right]\)
(4) 当以矩阵\(A\)为自变量时,求 \(P(x)\) 的值。其中A的值与(3)相同。
%(1)
p1=[1,2,4,0,5];
p2=[1,2];
p3=[1,2,3];
p4=[0,conv(p2,p3)];%求结果
p=p1+p4
%(2)
y=roots(p)
%(3)
A=[-1,1.2,-1.4;0.75,2,3.5;0,5,2.5;];
y1=polyval(p,A)%x取矩阵A的每一元素
%(4)
y2=polyvalm(p,A)
| 运行结果 |
|---|
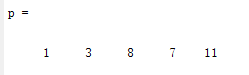 |
 |
 |
 |


