[USACO 08MAR]土地购买 Land Acquisition
[USACO08MAR] 土地购买 Land Acquisition
1.题目
题目描述
约翰准备扩大他的农场，眼前他正在考虑购买N块长方形的土地。如果约翰单买一块土地，价格就是土地的面积。但他可以选择并购一组土地，并购的价格为这些土地中最大的长乘以最大的宽。比如约翰并购一块3 × 5和一块5 × 3的土地，他只需要支付5 × 5 = 25元， 比单买合算。 约翰希望买下所有的土地。他发现，将这些土地分成不同的小组来并购可以节省经费。 给定每份土地的尺寸，请你帮助他计算购买所有土地所需的最小费用。
输入输出格式
输入格式：
Line 1: A single integer: N
Lines 2..N+1: Line i +1 describes plot i with two space-separated integers: \(width_{i}\) and \(length_i\)
输出格式：
Line 1: The minimum amount necessary to buy all the plots.
输入输出样例
输入样例#1：
复制
4 100 1 15 15 20 5 1 100输出样例#1：
500说明
There are four plots for sale with dimensions as shown.
The first group contains a 100x1 plot and costs 100. The next group contains a 1x100 plot and costs 100. The last group contains both the 20x5 plot and the 15x15 plot and costs 300. The total cost is 500, which is minimal.
2.题解
这题可以使用斜率优化。设长为\(l\)，宽为\(r\)。
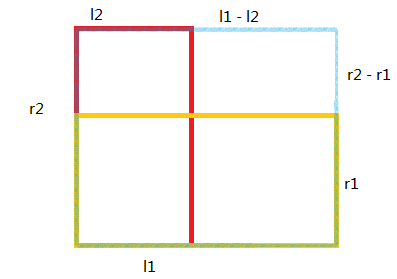
当考虑矩形1与矩形2组合时，则花费为\(l1 \times r2\)。需要额外承担的花费为\((l1 - l2) * (r2 - r1)\)。所以在转移时我们需要考虑两正方形之间长与宽的差的绝对值最小。所以按照先长升序后宽升序排序。
这样我们就得到了一个长递增，宽之间关系不确定的序列。再考虑当\(i > j\)，若\(l_{i} > l_{j}\)且\(w_{i} > w_{j}\)，则矩形\(i\)一定包含矩形\(j\)。这样我们可以预处理一下，将被包含的矩形去除掉，不需要再DP。这样，在矩形\(i\)前且\(w_{j} < w_{i}\)的矩形就被处理没了，我们就获得了一个长递增，宽递减的序列，转移式就非常好写了。
#include <algorithm>
#include <cstdio>
typedef long long ll;
const int MAXN = 50010;
struct LAND{
int l, w;
}a[MAXN];
int n, tmpn;
ll f[MAXN];
inline bool cmp(LAND a, LAND b) { //排序
return (a.l == b.l ? a.w < b.w : a.l < b.l);
}
inline double slope(int i, int j) {
return ((f[j] - f[i]) / (1.0 * (a[j + 1].w - a[i + 1].w)));
}
struct QUEUE {
int head, tail;
int q[MAXN];
QUEUE() {head = tail = 0;}
void clean() {head = tail = 0;}
void push(int x) { //斜率是负数，所以与普通下凸包维护操作不同
while(head <= tail && slope(q[tail], x) > slope(q[tail - 1], q[tail])) tail--;
q[++tail] = x;
}
int pop(int i) {
int tmp = -a[i].l;
while(head < tail && slope(q[head], q[head + 1]) > tmp) head++;
return q[head];
}
}que;
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i)
scanf("%d%d", &a[i].w, &a[i].l);
std::sort(a + 1, a + n + 1, cmp);
for (int i = 1; i <= n; ++i) { //处理被包含的矩形
while(tmpn && a[tmpn].w <= a[i].w) tmpn--;
a[++tmpn] = a[i];
}
n = tmpn;
for (int i = 1; i <= n; ++i) {
int j = que.pop(i);
f[i] = f[j] + (ll)a[i].l * a[j + 1].w;
que.push(i);
}
printf("%lld\n", f[n]);
return 0;
}
因为斜率是负数，所以虽然要维护下凸包，但是\(slope(tail, i) < slope(tail - 1,tail)\)，\(slope(head, head+1) < k\)，我就栽在这里了一定要注意。
