如何判断数据是否满足正态分布

方法：P-P图、Q-Q图、DW检验(杜宾-瓦特森检验)

Q-Q图

分位数图示法（Quantile Quantile Plot，简称 Q-Q 图）

统计学里Q-Q图（Q代表分位数）是一个概率图，用图形的方式比较两个概率分布，把他们的两个分位数放在一起比较。首先选好分位数间隔。图上的点（x,y）反映出其中一个第二个分布（y坐标）的分位数和与之对应的第一分布（x坐标）的相同分位数。因此，这条线是一条以分位数间隔为参数的曲线。如果两个分布相似，则该Q-Q图趋近于落在y=x线上。如果两分布线性相关，则点在Q-Q图上趋近于落在一条直线上，但不一定在y=x线上。Q-Q图可以用来可在分布的位置-尺度范畴上可视化的评估参数。
从定义中可以看出Q-Q图主要用于检验数据分布的相似性，如果要利用Q-Q图来对数据进行正态分布的检验，则可以令x轴为正态分布的分位数，y轴为样本分位数，如果这两者构成的点分布在一条直线上，就证明样本数据与正态分布存在线性相关性，即服从正态分布

P-P图

P-P图是根据变量的累积概率对应于所指定的理论分布累积概率绘制的散点图，用于直观地检测样本数据是否符合某一概率分布。如果被检验的数据符合所指定的分布，则代表样本数据的点应当基本在代表理论分布的对角线上。
由于P-P图和Q-Q图的用途完全相同，只是检验方法存在差异。要利用QQ图鉴别样本数据是否近似于正态分布,只需看QQ图上的点是否近似地在一条直线附近,而且该直线的斜率为标准差,截距为均值.

具体用python作图步骤

1、将样本数据从小到大排序，假设排序后的样本数据为\(x_{1}\),\(x_{2}\),\(x_{3}\),...,\(x_{n}\).

2、对于\(n\)个样本数据，对应\(n\)个分位数。分位数的取值规则不一样，一个比较简答的规则是:第\(k\)个分位数的取值为\(Q_{k} = ( k − 0.5 )/n\).

3、横坐标为：\(x_{1}\),\(x_{2}\),\(x_{3}\),\(\dots\)，\(x_{n}\),纵坐标为：所判断分布的累计分布函数在分位数的逆函数值 \(F−(Q_{k} )\)，则为 QQ 图；若横坐标为:\(F_(x_{1})\),\(F(x_{2})\),\(F(x_{3})\),\(\dots\),\(F(x_{n})\)，纵坐标为：\(Q_{k}\) ,则为 PP 图。

PP 图与 QQ 图的功能基本一样，我见用 QQ 图的比较多。因为分位数的取值规则不一样，因此 QQ 图可能画的不太一样。

下面以正态分布的随机样本为例，用 python 画一下图形，专门的 QQ 图也可以调用 statsmodels 中的 ProbPlot 函数 (不是 scipy 中的 probplot，因为 scipy 中的 probplot 画的直线是拟合直线，并不是45度斜线)。

from scipy import stats
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np

df = [33,23,35,35.5,26,32.3,41,29,38.5,42,31,54.2,43,
      34,26.5,27,37,40.1,30,39.5,28,36.5,43,45,31,
      46.3,42.8,52.1,49,49,40,52.7,39,48.1,35,58,
      32,31.5,37,28,19,34.3,38,59.5,32.8,43,33,50,48,46]
sorted_ = np.sort(df)
yvals = np.arange(len(sorted_))/float(len(sorted_))
x_label = stats.norm.ppf(yvals)  #对目标累计分布函数值求标准正太分布累计分布函数的逆
plt.style.use('ggplot')
stats.probplot(df, dist="norm",plot=plt)  #画QQ图
plt.show()

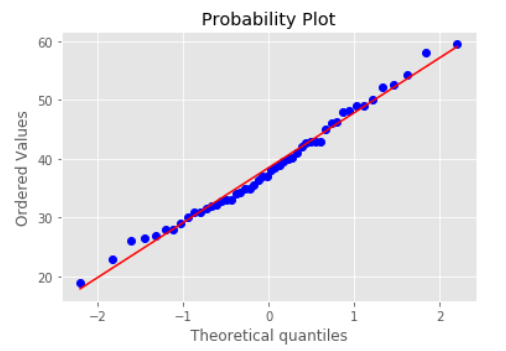
红色线条表示正态分布，蓝色线条表示样本数据，蓝色越接近红色参考线，说明越符合预期分布（这是是正态分布）

Q-Q图是通过比较数据和正态分布的分位数是否相等来判断数据是不是符合正态分布

由于 ProbPlot 的分位数取值规则不同，ProbPlot 的QQ图与自己画的QQ图略微不一样

小样本使用SW检验，大样本使用K-S检验。K-S检验可以做修正来减小样本偏差，修正具体是实际和理论概率累积量的max偏差值与零相比。
用QQ图还可获得样本偏度和峰度的粗略信息.

参考网页
https://www.cnblogs.com/king-lps/p/7840268.html
https://www.cnblogs.com/yuanjingnan/p/11668547.html
https://blog.csdn.net/robert_chen1988/article/details/106278793
https://blog.csdn.net/lvla_juan/article/details/97235734