算法(一):算法概述
1.算法的概念
1.1.算法的定义
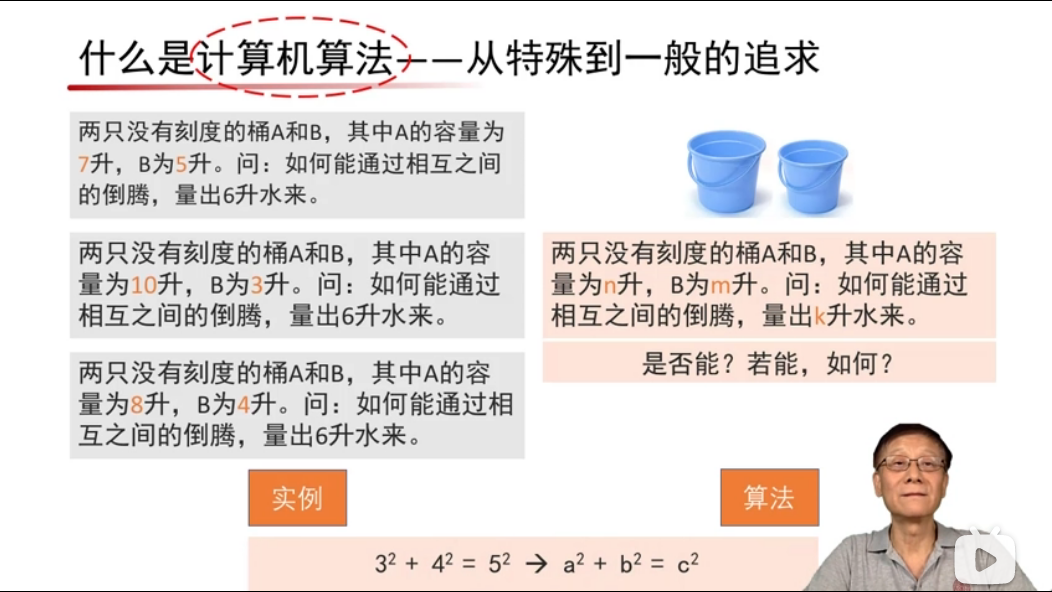
算法是解决问题的一系列操作步骤,而计算机算法要具有一般性,而非只适用于一些特殊实例。
1.2.算法的求解
从实例开始,一步一步解决问题,最终得到算法。
2.算法的描述
算法的描述就是用自然语言、流程图、伪代码这几种方式,以及顺序结构、 分支结构、 循环结构这三种控制结构来将问题求解的操作步骤描述出来。
算法描述有以下优点:
- 让目标读者看得懂;
- 便于分析算法的性质;
- 有助于程序的实现。
3.算法的分析
3.1.正确性
是否能得到预期输出。
3.2.健壮性
当输入非法数据时,算法恰当地做出反应或者进行相应的处理,而不是给出一个莫名奇妙的结果。
处理数据的方法错误时,不应是中断程序的执行,而应是返回一个表示错误的值,以便在更高的抽象层次上进行处理。
3.3.高效性
a.时间效率
事后分析法就是让算法运行起来,然后看运行的时间。
事前分析法就是算法的运行时间=所有语句的执行次数*一条语句的执行时间。由于一条语句的执行时间随着硬件的不同而不同,因此我们假设一条语句的执行时间均为单位时间,从而让算法的运行时间只和语句的执行次数有关。
为了便于比较不同算法之间的差异,我们取一个辅助函数f(n),使得当n无穷大时,T(n) / f(n)的极限值为不等于零的常数,此时记T(n) = O(f(n)),称 O(f(n))为算法的渐近时间复杂度。简而言之,时间复杂度就是执行次数T(n)关于数据规模n的函数,记T(n) = O(f(n))。
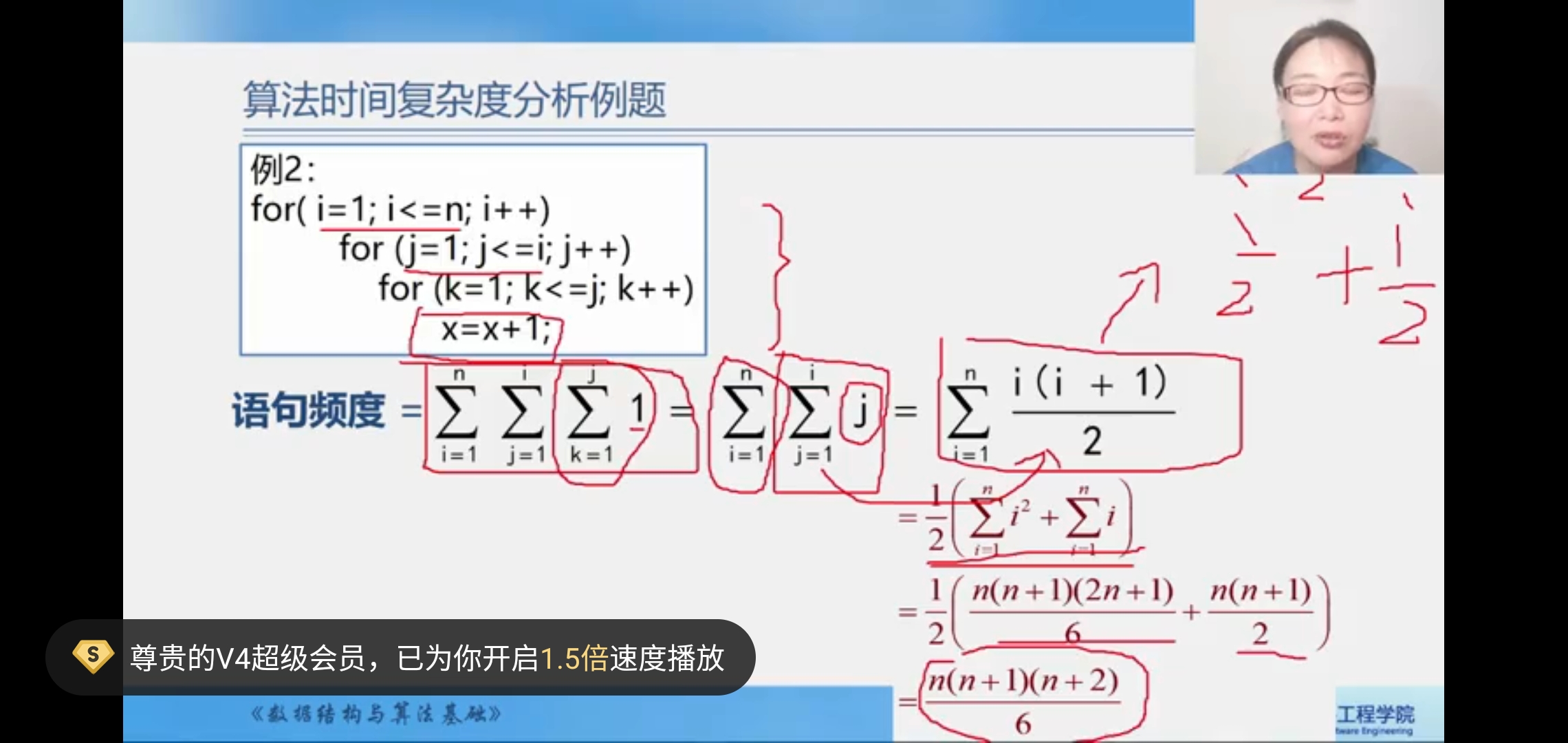
- 时间复杂度的计算方法为:先找出语句频度最大的作为基本语句;再计算基本语句的执行次数和问题规模n之间的关系f(n)(在计算f(n)时,如果不好计算可以使用级数来计算,也可以使用加法法则和乘法法则);最后取其数量级用符号O表示。
-
![hbAk7j.jpg]()
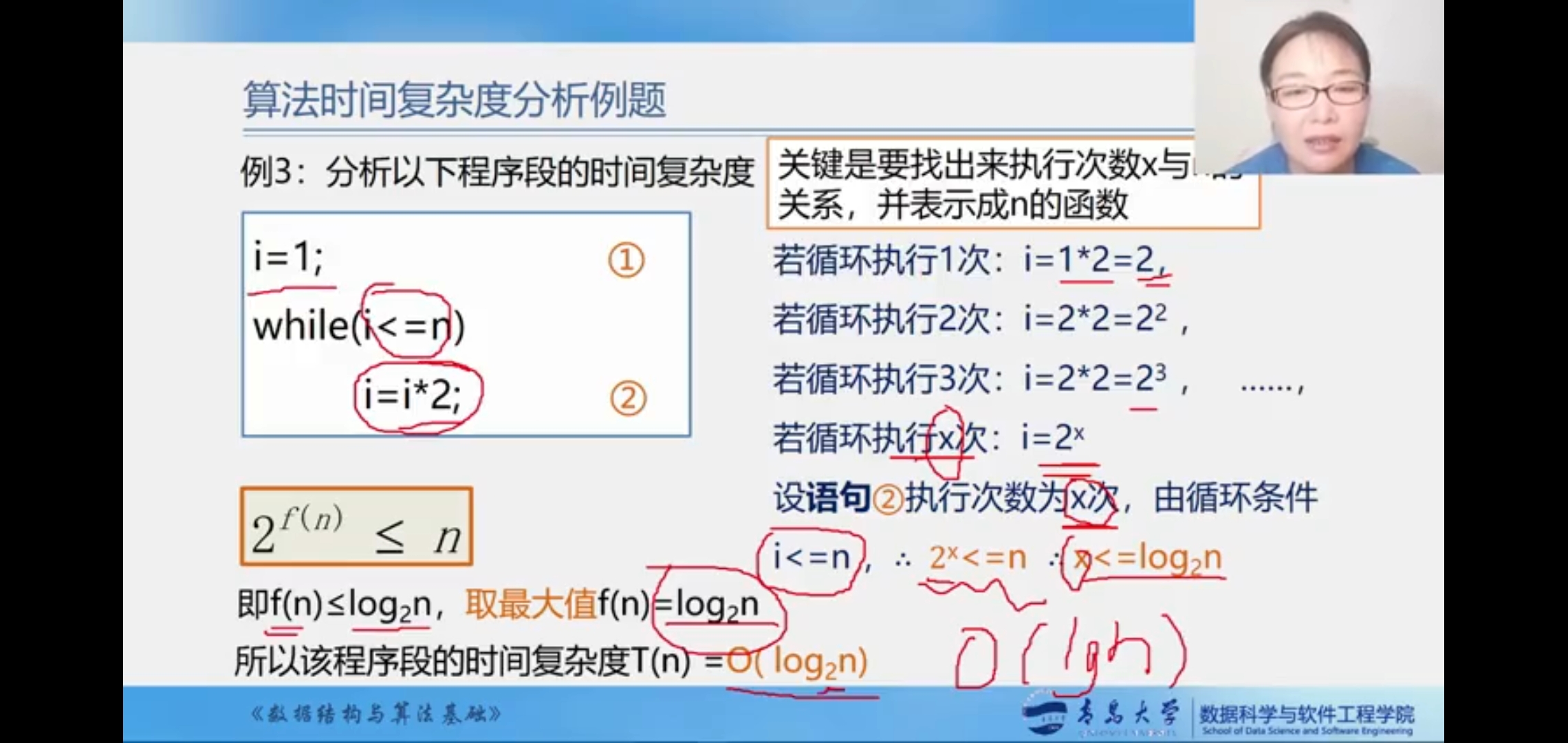
-
![hbAhDg.jpg]()
由于算法的执行次数还和数据集有关,因此存在着算法时间复杂度的最好、平均、最坏三种情况,一般来说我们只考虑最坏情况下的时间复杂度。
b.空间效率
算法的空间效率就是算法要占据的内存空间。我们也有事前分析法和事后分析法。
事后分析法就是空间效率就是算法使用的辅助空间。
类似的,使用S(n) = O(f(n)),将O(f(n))称为算法的空间复杂度。
3.4.可读性
a.代码规范
命名:大驼峰命名法、小驼峰命名法、下划线法、匈牙利命名法。
b.设计模式
4.算法的分类
4.1.按设计思想分
- 穷举算法
- 动态规划算法
- 分治算法
- 贪心算法
- 启发算法
- 回溯算法
4.2.按效率分
- O(1)、O(logn)、O(n)、O(n^2)、O(n!)
4.3.按应用场合分
- 数值算法:主要目的在于模拟与仿真。
- 非数值算法:主要目的在于搜索、推理、决策、规划等。
4.4.按数据存在的介质分
- 内存算法
- 外存算法
本文来自博客园,作者:曼路的个人博客,转载请注明原文链接:https://www.cnblogs.com/manlujun/p/15642357.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号