观景房

观景房

题意

给出若干个矩形，所有矩形组合形成的图形包含了若干条水平线。

你可以选出若干条水平线，必须满足高度先上升后下降，求选出的水平线长度和的最大值。

思路

先考虑如何求出所有水平线的高度和长度，观察下面的图片。

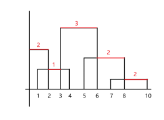
每个位置的水平高度就是覆盖这个位置的矩形高度最大值。

我们就需要一个数据结构支持以下操作：

1. 区间修改，给定 \(l,r,v\)，\(a_i \leftarrow \max \left \{a_i,v \} \right.(i \in [l,r])\)。

2. 单点查询 \(a_i\) 的值。

可以使用线段树维护。

每个线段树节点打一个标记，存这个节点被整体取 \(\max\) 的数。

查询时从叶子结点往根节点回溯时，把答案对当前节点标记取 \(\max\)。

得到每个位置的高度后，极长的一段高度相等的位置就是一条水平线，记录长度就行了。

完成这步后，发现这个问题很像最长上升子序列，可以对水平线进行 \(dp\)。

定义 \(f_{i,0/1}\) 表示考虑前 \(i\) 条水平线，从上一条水平线到这一条是上升了/下降了。

记 \(l_i\) 为第 \(i\) 条水平线的长度，\(h_i\) 为第 \(i\) 条水平线的高度。

转移方程：

\[\left\{ \begin{matrix} f_{i,0}=\max_{j<i,h_j \le h_i} \left \{ f_{j,0}\} \right.+l_i \\ f_{i,1}=\max_{j<i,h_j \ge h_i} \left \{ f_{j,0},f_{j,1} \} + l_i \right. \end{matrix} \right. \]

暴力转移时间复杂度是 \(O(n^2)\) 的，考虑优化。

\(j<i\) 这一条件通过从小到大的枚举顺序可以消除，每个位置从前面转移就行。

每次求 \(h_j\le h_i\) 的最大值不就是区间查询 \([1,h_i]\) 的最大值吗？

每次算出一个 \(f\) 值不就是单点修改 \(h_i\) 对应的最大值吗？

单点修改，区间查询，可以使用线段树维护。

转移时从当前对应的值域区间求出 \(f\) 的最大值，

转移后更新当前 \(h\) 对应位置的最大值。

开两棵线段树，一棵维护 \(f_{i,0}\) 一棵维护 \(f_{i,1}\)。

时间复杂度：\(O(n\log n)\)。

代码

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int N = 1e6 + 7;
const int W = 1e6 + 2;

struct segt {
	struct node {
		int l, r, tag;
	} t[N << 2]; 
	#define ls (p << 1)
	#define rs (p << 1 | 1)
	void build(int p, int l, int r) {
		t[p].l = l, t[p].r = r, t[p].tag = 0;
		if (l == r) return ;
		int mid = (l + r) >> 1;
		build(ls, l, mid);
		build(rs, mid + 1, r);
	}
	void modify(int p, int l, int r, int v) {
		if (l <= t[p].l && t[p].r <= r) {
			t[p].tag = max(t[p].tag, v);
			return ;
		}
		if (l <= t[ls].r) modify(ls, l, r, v);
		if (r >= t[rs].l) modify(rs, l, r, v);
	}
	int query(int p, int id) {
		if (t[p].l == t[p].r) return t[p].tag;
		if (id <= t[ls].r) return max(t[p].tag, query(ls, id));
		return max(t[p].tag, query(rs, id));
	}
} T; // 区间取max线段树

struct segt1 {
	struct node {
		int l, r, v;
	} t[N << 2]; 
	#define ls (p << 1)
	#define rs (p << 1 | 1)
	void build(int p, int l, int r) {
		t[p].l = l, t[p].r = r, t[p].v = 0;
		if (l == r) return ;
		int mid = (l + r) >> 1;
		build(ls, l, mid);
		build(rs, mid + 1, r);
	}
	void modify(int p, int id, int v) {
		if (t[p].l == t[p].r) {
			t[p].v = max(t[p].v, v);
			return ;
		}
		if (id <= t[ls].r) modify(ls, id, v);
		else modify(rs, id, v);
		t[p].v = max(t[ls].v, t[rs].v);
	}	
	int query(int p, int l, int r) {
		if (l > r) return 0;
		if (l <= t[p].l && t[p].r <= r) return t[p].v;
		int res = 0;
		if (l <= t[ls].r) res = max(res, query(ls, l, r));
		if (r >= t[rs].l) res = max(res, query(rs, l, r));
		return res;
	}
} Tf0, Tf1; // 区间求max线段树


int n, m, X1[N], X2[N], h[N], a[N];
int b[N], f[N][2], ans;

signed main() {
	freopen("see.in", "r", stdin);
	freopen("see.out", "w", stdout);
	
	cin >> n;
	T.build(1, 1, W);
	for (int i = 1; i <= n; i ++) {
		cin >> X1[i] >> X2[i] >> h[i]; 
		X1[i] ++, X2[i] ++; // 避免0的情况
		T.modify(1, X1[i] + 1, X2[i], h[i]); // 维护水平线高度
	}
	
	for (int i = 1; i <= W; i ++) 
		a[i] = T.query(1, i); // 求水平线高度

	for (int i = 1; i <= W; ) { // 求水平线长度
		int j = i; m ++;
		while (j < W && a[j + 1] == a[j]) j ++;
		b[m] = j - i + 1;
		i = j + 1; 
	}
	
	
	unique(a + 1, a + W + 1);
	
	Tf0.build(1, 1, W);
	Tf1.build(1, 1, W);
	
	for (int i = 2; i < m; i ++) {
		f[i][0] = Tf0.query(1, 1, a[i]) + b[i]; // 根据方程转移
		f[i][1] = max(Tf0.query(1, a[i], W), Tf1.query(1, a[i], W)) + b[i];
		Tf0.modify(1, a[i], f[i][0]); // 更新dp值
		Tf1.modify(1, a[i], f[i][1]);
		ans = max({ans, f[i][0], f[i][1]});
	} 
	
	cout << ans << "\n"; 
	return 0;
}