[COCI2020-2021#5] Po

[COCI2020-2021#5] Po

题意

给出一个序列 \(a\)，有一个序列 \(b\)，初始全为 \(0\)。

可以对序列 \(b\) 进行如下操作：使一个连续的区间内的所有数加上一个正整数 \(x\)。

但要求任意两个操作区间要么互不相交，要么一个包含另外一个。

求将序列 \(b\) 变为序列 \(a\) 的最小操作次数。

思路

使用单调递增栈维护。

对于新来的一个数：

若它比所有数都大，则入栈，答案加一。

否则，弹栈直到栈顶不大于它。

因为这些数对以后的数都没用了，如下图。

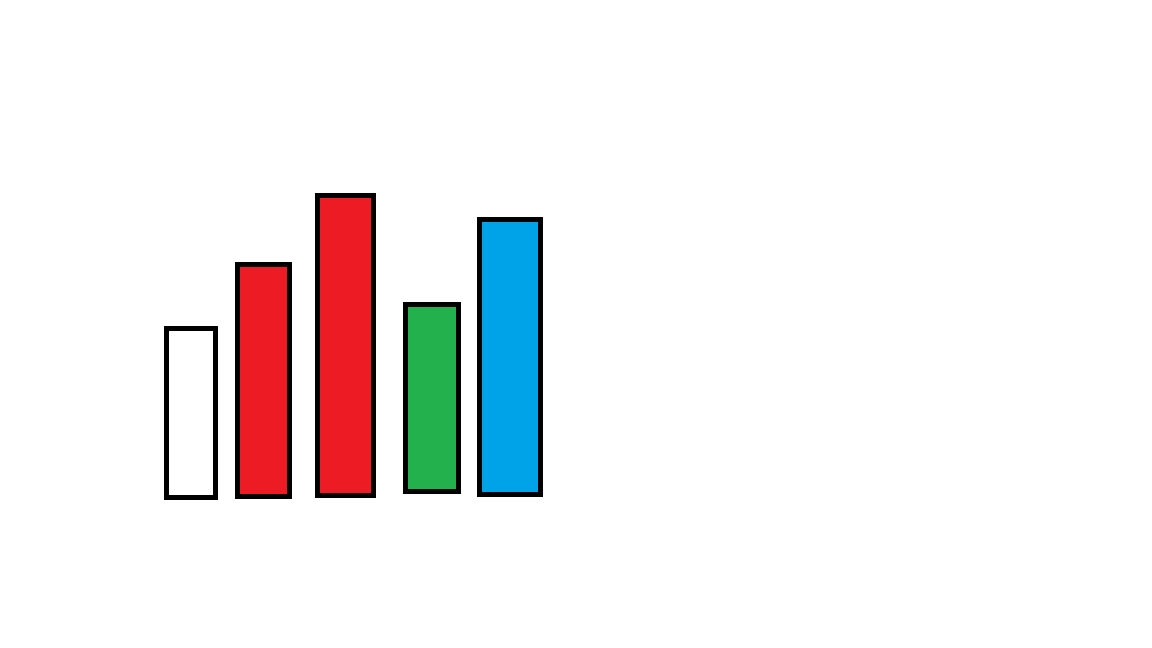
红色柱子和蓝色柱子在一个区间中加的高度一定不超过绿色柱子，

所以两个红色柱子就没有贡献了，弹出即可。

然后将当前数入栈，将答案加一。

特别地，若栈顶等于当前数，答案不加一。

因为最优情况下，造出那个数时，当前数也被造出了。

代码

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5 + 5;
int n, a[N], ans;
int top, stk[N];
void solve() {
	cin >> n;
	for (int i = 1; i <= n; i ++) cin >> a[i];
	stk[++ top] = 0;
	for (int i = 1; i <= n; i ++) {
		while (top && a[i] < stk[top]) top --;
		if (top && stk[top] == a[i]) continue;
		stk[++ top] = a[i], ans ++;
	}
	cout << ans << "\n";
}
signed main() {
	int T = 1;
//	cin >> T;
	while (T --)
		solve(); 
	return 0;
}