Atcoder Beginner Contest 365

Atcoder Beginner Contest 365

A

题意

输入年份，输出该年份天数。

思路

略

B

题意

输入一个序列，输出该序列次大值的位置。

思路

略

C

题意

给定 $N$，序列 $A$ 和 $M$。

求满足下条件的 $x$ 最大值。

$$\sum _{i=1}^{n}min(x,A_i)\le M$$

思路

式子左边有单调性，二分 $x$ 即可。

D

题意

两个人玩剪刀石头布，给出第一个人的动作。

第二个人不能输给第一个人（平局或赢），不能连续做两个相同的动作。

求第二个人最大赢的次数。

思路

动态规划。

状态：$d{p}_{i,j}$ 表示前 $i$ 回合，第 $i$ 回合出 $j$ 最大赢的次数。

枚举 $i$ 的动作和 $i-1$ 的动作转移即可。

E

题意

给定 $N$ 和序列 $A$，求：

$$\sum _{i=1}^{n-1}\sum _{j=i+1}^n\underset{k=i}{\overset{j}{⨁}}{A}_k$$

思路

按位考虑，把序列转化成只有 $0$ 和 $1$ 的序列。

枚举 $i$，考虑如何求出所有以 $i$ 为左端点的答案。

因为序列只有 $0$ 和 $1$，只有异或后结果为 $1$ 对答案才有贡献。

问题转化成：

$$\sum _{i=1}^{n-1}\sum _{j=i+1}^n[\underset{k=i}{\overset{j}{⨁}}{A}_k=1]$$

考虑倒序枚举 $i$，统计对于当前 $i$ 的符合条件的 $j$ 个数。

维护两个值。

$$o=\sum _{j=i+1}^n[\underset{k=i}{\overset{j}{⨁}}{A}_k=1]$$

$$z=\sum _{j=i+1}^n[\underset{k=i}{\overset{j}{⨁}}{A}_k=0]$$

当 $A_i=0$ 时，统计答案，将 $z$ 加一。

当 $A_i=1$ 时，交换 $o,z$，统计答案，将 $o$ 加一。

因为当 $A_i=1$ 时，原来对于 $i+1$ 的 $z$ 异或上当前的 $1$ 就变成当前 $o$，当前 $z$ 同理。

统计答案时记得乘上位权。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e5 + 5;
int n, a[N];
ll ans, one, zero;
void solve() {
    cin >> n;
    for (int i = 1; i <= n; i ++) cin >> a[i];
    for (int j = 0; j <= 30; j ++) {
        zero = one = 0;
        for (int i = n; i >= 1; i --) {
            if (a[i] >> j & 1) swap(zero, one);
            ans += one * (1 << j);
            zero += !(a[i] >> j & 1);
            one += (a[i] >> j & 1);
        }
    }
    cout << ans << "\n";
}
int main() {
    int T = 1;
    // cin >> T;
    while (T --) solve();
    return 0;
}

F

题意

给定一张地图，对于第 $i$ 列（$1\le i\le N$），当且仅当 $j\in [L_i,U_i]$ 的时候 $(i,j)$ 为空格子，其他格子均为障碍。

现在有 $Q$ 个询问。每个询问给定起点和终点坐标，求最少的移动步数。

保证给出的起点和终点的坐标为空格子。

思路

线段树。

发现一段区间的区间可以分为两种：

0. 所有区间有交集，可以走到交集上一路向右。

1. 所有区间无交集，需要拐弯。

如下图，左边为 $0$ 区间，右边为 $1$ 区间。

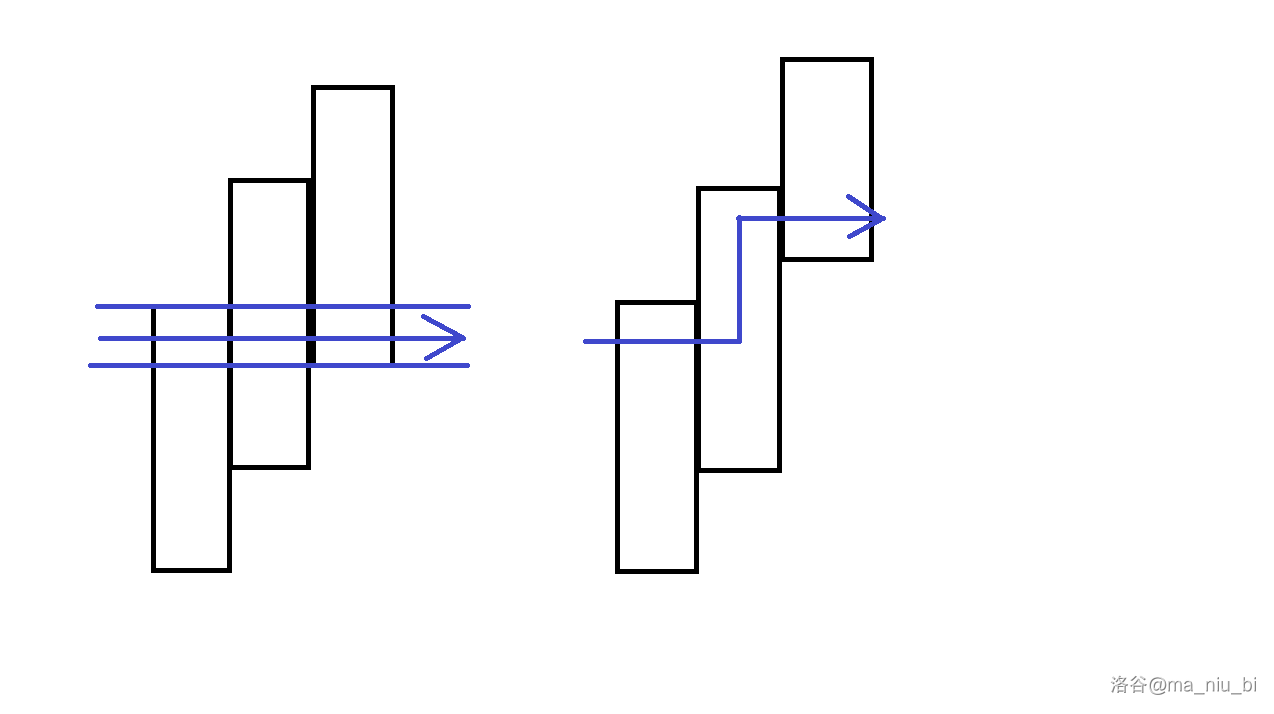
可以使用线段树维护区间信息。

节点 $[l,r]$ 维护一以下信息。

0. 区间类型

1. 区间交集

2. 区间起点

3. 区间终点

4. 区间从起点到终点的最短路

区间起点指从 $l$ 出发，无论从哪个点出发，经过起点一定不劣。

区间终点指到 $r$ 结束，无论到哪个点结束，经过终点一定不劣。

$0$ 区间不存在区间起/终点。

$1$ 区间不存在区间交集。

合并节点时分类讨论：

0. 两个 $0$ 合并，若还有交集，结果还是 $0$。最短路没有贡献。

1. 两个 $0$ 合并，若没有交集，结果变为 $1$。最短路贡献为两个区间的最短距离，区间起点/终点为使距离最短的两个点。可以发现这两个点要么是左儿子的右端点和右儿子的左端点，要么是左儿子的左端点和右儿子的右端点，分类讨论是哪种。容易发现若左儿子在下，右儿子在上，为前者，否则为后者。

2. 一个 $1$ 和一个 $0$ 合并，结果为 $1$。若 $1$ 区间起/终点在 $0$ 区间交集内，最短路贡献为 $0$，新的起/终点为 $1$ 区间起/终点。否则，最短路贡献为 $0$ 区间到 $1$ 区间起/终点的最小距离，更新起/终点与 $2$ 类似讨论即可。

3. 两个 $1$ 合并，结果还是 $1$。最短路贡献为左儿子终点到右儿子起点的距离，区间起点为左儿子起点，区间终点为右儿子终点。

统计答案时在线段树上查询出区间信息，对于真正的起/终点和区间的位置关系分类讨论，加上对应贡献。

0. 若区间为 $1$，贡献为起点到区间起点的距离加上终点到区间终点的距离。

1. 若区间为 $0$，起/终点都在交集中，直接加上起点到终点的距离。

2. 若区间为 $0$，起/终点在交集异侧，直接加上起点到终点的距离。

3. 若区间为 $0$，起/终点在交集同侧，若起/终点同在区间上方，加上起/终点到右端点的距离，若起/终点同在区间下方，加上起/终点到左端点的距离。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e5 + 5;
int n, q, U[N], V[N];   
bool check(pair <int, int> a, pair <int, int> b, pair <int*, int*> c) {
    if (a.first > b.first) swap(a, b);
    if (b.first > a.second) {
        *c.first = -1;
        *c.second = -1;
        return 0;
    }
    *c.first = max(a.first, b.first);
    *c.second = min(a.second, b.second);
    return 1;
}
struct segt {
    struct node {
        int l, r;
        int type;
        int L, R;
        int in, out;
        ll dis;
    } t[N << 2];
    #define ls (p << 1)
    #define rs (p << 1 | 1)
    friend node operator + (node a, node b) {
        node res;
        res.l = a.l, res.r = b.r;
        if (!a.type && !b.type) {
            if (check({a.L, a.R}, {b.L, b.R}, {&res.L, &res.R})) {
                res.type = 0;
                res.in = res.out = -1;
                res.dis = a.dis + b.dis;
            } else {
                res.type = 1;
                if (a.L > b.R) res.in = a.L, res.out = b.R;
                else res.in = a.R, res.out = b.L;
                res.dis = a.dis + b.dis + abs(res.in - res.out);
            }
        } else if (!a.type) {
            res.type = 1;
            res.out = b.out;
            res.dis = a.dis + b.dis;
            res.L = res.R = -1;
            if (a.L <= b.in && b.in <= a.R) {
                res.in = b.in;
            } else {
                if (b.in > a.R) {
                    res.in = a.R;
                    res.dis += b.in - a.R;
                } else if (b.in < a.L) {
                    res.in = a.L;
                    res.dis += a.L - b.in;
                }
            }
        } else if (!b.type) {
            res.type = 1;
            res.in = a.in;
            res.dis = a.dis + b.dis;
            res.L = res.R = -1;
            if (b.L <= a.out && a.out <= b.R) {
                res.out = a.out;
            } else {
                if (a.out > b.R) {
                    res.out = b.R;
                    res.dis += a.out - b.R;
                } else if (a.out < b.L) {
                    res.out = b.L;
                    res.dis += b.L - a.out;
                }
            }
        } else {
            res.type = 1;
            res.in = a.in, res.out = b.out;
            res.L = res.R = -1;
            res.dis = a.dis + b.dis + abs(a.out - b.in);
        }
        return res;
    }
    void build(int p, int l, int r) {
        t[p].l = l, t[p].r = r;
        if (l == r) {
            t[p].type = 0;
            t[p].L = U[l];
            t[p].R = V[l];
            t[p].in = t[p].out = -1;
            t[p].dis = 1;
            return ;
        }
        int mid = (l + r) >> 1;
        build(ls, l, mid);
        build(rs, mid + 1, r);
        t[p] = t[ls] + t[rs];
    }
    node query(int p, int l, int r) {
        if (l <= t[p].l && t[p].r <= r) return t[p];
        node res; res.l = -1;
        if (t[ls].r >= l) res = query(ls, l, r);
        if (t[rs].l <= r) {
            if (res.l == -1) res = query(rs, l, r);
            else res = res + query(rs, l, r);
        }
        return res;
    }
} T;
void solve() {
    cin >> n;
    for (int i = 1; i <= n; i ++) cin >> U[i] >> V[i];
    T.build(1, 1, n);
    cin >> q;
    while (q --) {
        int sx, sy, tx, ty;
        cin >> sx >> sy >> tx >> ty;
        if (sx > tx) {
            swap(sx, tx);
            swap(sy, ty);
        }
        segt::node res = T.query(1, sx, tx);
        if (!res.type) {
            if (!(res.L <= sy && sy <= res.R) && !(res.L <= ty && ty <= res.R)) {
                if (sy < res.L && ty > res.R || ty < res.L && sy > res.R) res.dis += abs(sy - ty);
                else if (sy < res.L && ty < res.L) res.dis += abs(sy - res.L) + abs(ty - res.L);
                else if (sy > res.R && ty > res.R) res.dis += abs(sy - res.R) + abs(ty - res.R);
            } else res.dis += abs(sy - ty);
        } else {
            res.dis += abs(sy - res.in) + abs(ty - res.out);
        }
        cout << res.dis - 1 << "\n";
    }
}
int main() {
    int T = 1;
    // cin >> T;
    while (T --) solve();
    return 0;
}

G

题意

有 $n$ 个人在办公室工作。

办公室的门有出入记录系统。现在共有 $m$ 条记录，每条记录由二元组 $(T_i,P_i)$ 组成，表示在 $T_i$ 的时间 $P_i$ 号人进入或走出办公室（若当时在外面即为进入，在里面即为出去）。

一开始所有人都在外面。

给定 $q$ 次询问，每次询问 $A_i$ 号和 $B_i$ 号人同时在办公室的时间。

思路

根号分治。

设定阀值 $B=\sqrt{m}$，将出现次数大于等于 $B$ 的人和小于 $B$ 的人分开处理。

出现次数大于等于 $B$ 的人不多于 $\frac{m}{B}=\sqrt{m}$ 个，使用前缀和统计出他们和所有人的答案，询问时直接输出，时间复杂度 $O(n\sqrt{m})$。

出现次数小于 $B$ 的人直接使用双指针统计答案，时间复杂度不大于 $O(\sqrt{m})$。

总时间复杂度：$O(n\sqrt{m})$。

总空间复杂度：$O(n\sqrt{(}m))$。

实现细节见代码。

代码

#include <bits/stdc++.h>
#define int ll
using namespace std;
typedef long long ll;
const int N = 2e5 + 5;
int n, m, q, B, P[N], T[N];
int tot, ans[505][N], sum[N], id[N];
vector <int> v[N];
void solve() {
    cin >> n >> m, B = sqrt(m);
    for (int i = 1; i <= m; i ++) {
        cin >> T[i] >> P[i];
        v[P[i]].push_back(i);
    }
    for (int i = 1; i <= n; i ++) {
        if (v[i].size() < B) continue;
        tot ++, id[i] = tot;
        for (int j = 1, st = 0; j <= m; j ++) {
            sum[j] = sum[j - 1];
            if (st) sum[j] += T[j] - T[j - 1];
            if (P[j] == i) st ^= 1;
        }
        for (int j = 1; j <= n; j ++) 
            for (int k = 1; k < v[j].size(); k += 2) 
                ans[tot][j] += sum[v[j][k]] - sum[v[j][k - 1]];
    }
    cin >> q;
    while (q --) {
        int a, b;
        cin >> a >> b;
        if (id[a]) cout << ans[id[a]][b] << "\n";
        else if (id[b]) cout << ans[id[b]][a] << "\n";
        else {
            int ANS = 0;
            for (int i = 1, p = 1; i < v[a].size(); i += 2) {
                while (p < v[b].size() && T[v[b][p]] < T[v[a][i]]) {
                    ANS += max(0ll, T[v[b][p]] - max(T[v[b][p - 1]], T[v[a][i - 1]]));
                    p += 2;
                }
                if (p < v[b].size())
                    ANS += max(0ll, T[v[a][i]] - max(T[v[b][p - 1]], T[v[a][i - 1]]));
            }
            cout << ANS << "\n";
        }
    }
}
signed main() {
    int Case = 1;
    // cin >> Case;
    while (Case --) solve();
    return 0;
}