树链剖分学习笔记

树链剖分学习笔记

简介

树链剖分是一种可以把树丢到线段树上维护的一种算法，时间复杂度为 \(O(n \log^2 n)\)。

思路

一、一些概念

1.重儿子：如果一个点有儿子，那么所有儿子中儿子最多的一个儿子就是这个点的重儿子。有点绕，可以看图理解。图中标红的点就是重儿子。

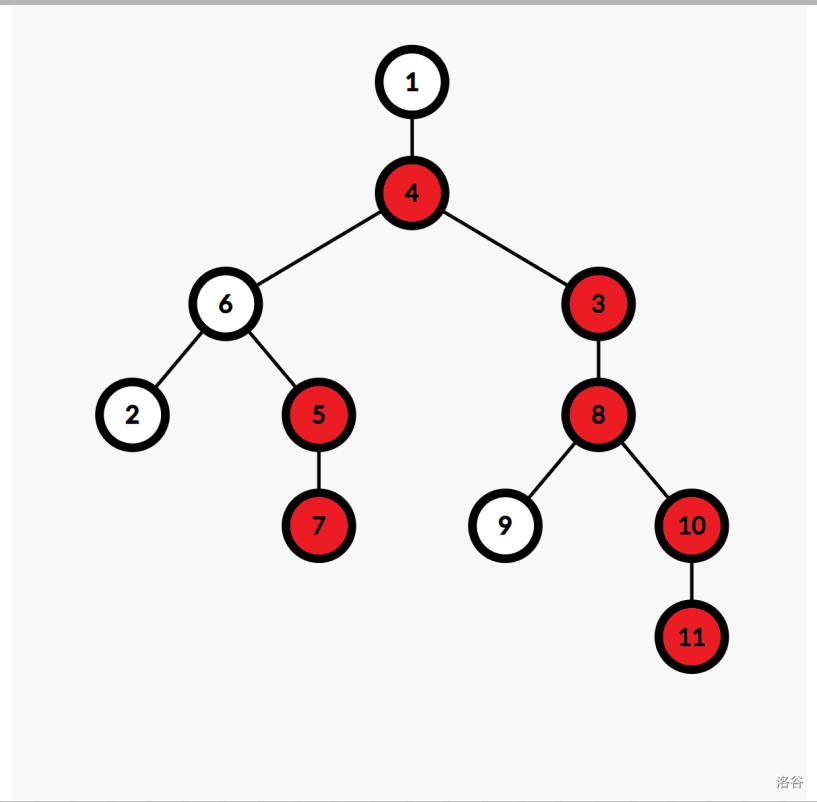
2.轻儿子：不是重儿子的点就是轻儿子。上图中白色的点就是轻儿子。

3.重链：由一个轻儿子开始，其他所有点都是重儿子的链。下图中红色的链就是重链。

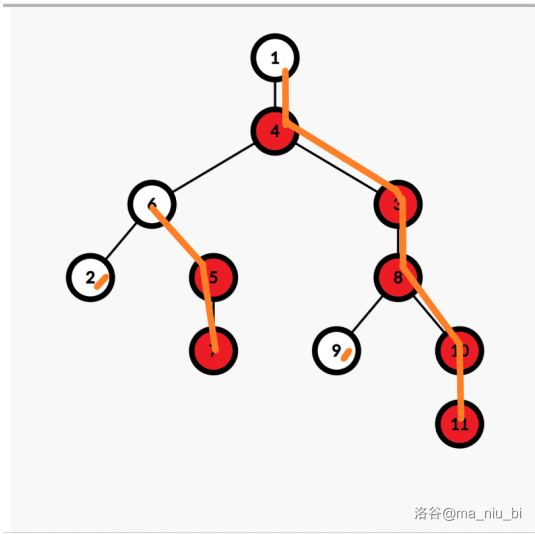
4.dfs序：从根开始，先dfs重儿子再dfs其他儿子，第几个被dfs到就是它的dfs序，下图中点旁边的数字就是dfs序。

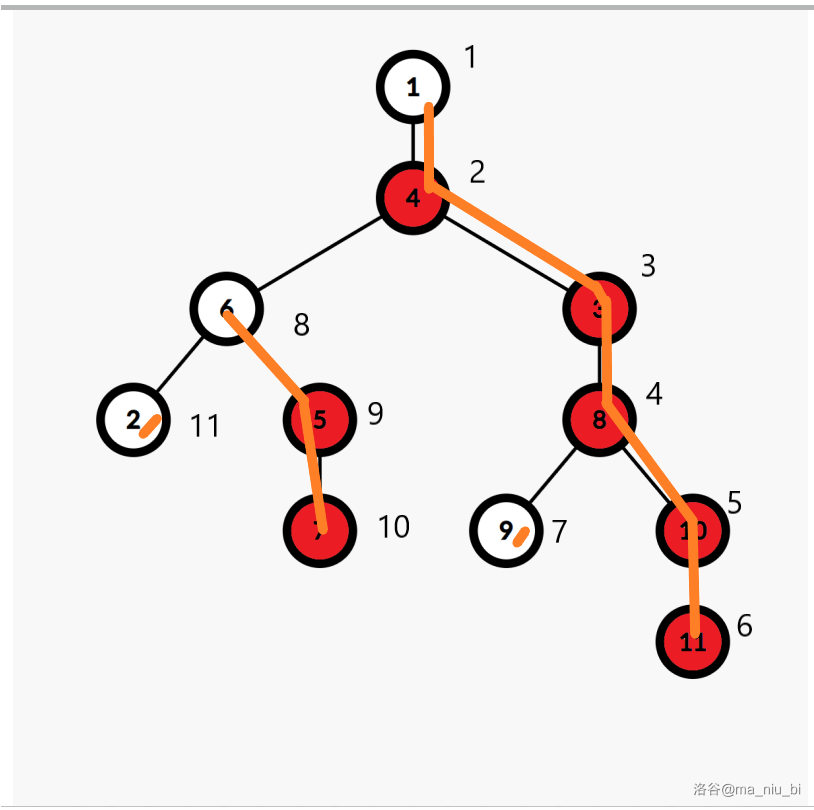
二、性质

有了这四个概念，再结合上面那张图，就可以发现一些有趣的性质

1.每一条重链上的dfs序是连续的。

2.每一棵子树里的dfs序也是连续的。

有了这些性质就可以把这棵树的dfs序扔到线段树里去了。

三、实现

1.求出重儿子，子树大小，父亲，深度（dfs1）

void dfs1(int x,int f){//de:深度,siz:子树大小,fa:父亲
	fa[x]=f,de[x]=de[fa[x]]+1,siz[x]=1;
	for(int i=head[x];i;i=nxt[i]){
		if(ver[i]==fa[x])continue;
		dfs1(ver[i],x);
		siz[x]+=siz[ver[i]];
		if(siz[ver[i]]>siz[son[x]])son[x]=ver[i];
	}
}

代码比较简单。

2.求出重链的起点和dfs序（dfs2）

void dfs2(int x,int f){//top:这个节点所在的重链的起点,dfn:dfs序,fdfn:dfs序对应的数
	top[x]=f,dfn[x]=++cnt,fdfn[cnt]=x;
	if(son[x]==0)return;
	dfs2(son[x],f);
	for(int i=head[x];i;i=nxt[i]){
		if(ver[i]==fa[x])continue;
		if(ver[i]==son[x])continue;
		dfs2(ver[i],ver[i]);
	}
}

代码也比较简单。

这样就可以把树放到线段树里维护啦！

例题

洛谷模板

这道题需要的操作是

• 1 x y z，表示将树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值都加上 \(z\)。

• 2 x y，表示求树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值之和。

• 3 x z，表示将以 \(x\) 为根节点的子树内所有节点值都加上 \(z\)。

• 4 x 表示求以 \(x\) 为根节点的子树内所有节点值之和

操作3和4可以通过性质2和线段树直接解决。

代码：

void x_subtree_add_z(int x,int z){
	tree.change(1,dfn[x],dfn[x]+siz[x]-1,z);
}
int ask_x_subtree(int x){
	return tree.ask(1,dfn[x],dfn[x]+siz[x]-1);
}

操作1和2：

树上两点的最短路径是：x->\(\text{lca}\)(x,y)->y。

我们可以用类似于跳lca的方法做，从一个点开始跳，每一次跳跳到这个重链的起点的父亲，直到两点在同一重链上，然后用线段树维护。

代码：

void x_to_y_add_z(int x,int y,int z){
	while(top[x]!=top[y]){
		if(de[top[x]]<de[top[y]])swap(x,y);//让更深一点的跳
		tree.change(1,dfn[top[x]],dfn[x],z);//先修改(x~top[x])
		x=fa[top[x]];//跳
	}
	if(de[x]<de[y])swap(x,y);//已经在同一条链上
	tree.change(1,dfn[y],dfn[x],z);//修改
}
int ask_x_to_y(int x,int y){//同理
	int ans=0;
	while(top[x]!=top[y]){
		if(de[top[x]]<de[top[y]])swap(x,y);
		ans=(ans+tree.ask(1,dfn[top[x]],dfn[x]));
		x=fa[top[x]];
	}
	if(de[x]<de[y])swap(x,y);
	ans=(ans+tree.ask(1,dfn[y],dfn[x]));
	return ans;
}

完整代码：

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=100005;
int MOD;
//------------------------------------------------------------以下为线段树模板
class SegmentTree{
	private:
		struct node{
			int l,r,data,add;
		}t[MAXN<<2];
		#define LSON (p<<1)
		#define RSON ((p<<1)|1)
		#define mid ((l+r)>>1)
		void make_lazy_tag(int p,int val){
			t[p].data=(t[p].data+(t[p].r-t[p].l+1)*val%MOD)%MOD;
			t[p].add=(t[p].add+val)%MOD;
		}
		void push_up(int p){
			t[p].data=(t[LSON].data+t[RSON].data)%MOD;
		}
		void push_down(int p){
			if(!t[p].add)return;
			make_lazy_tag(LSON,t[p].add);
			make_lazy_tag(RSON,t[p].add);
			push_up(p);
			t[p].add=0;
		}
	public:
		void build(int p,int l,int r,int* a,int* b){
			t[p].l=l,t[p].r=r;
			if(l==r){
				t[p].data=a[b[l]]%MOD;
				return;
			}
			build(LSON,l,mid,a,b);
			build(RSON,mid+1,r,a,b);
			push_up(p);
		}
		void change(int p,int l,int r,int val){
			if(l<=t[p].l&&t[p].r<=r){
				make_lazy_tag(p,val);
				return;
			}
			push_down(p);
			if(t[LSON].r>=l)change(LSON,l,r,val);
			if(t[RSON].l<=r)change(RSON,l,r,val);
			push_up(p);
		}
		int ask(int p,int l,int r){
			if(l<=t[p].l&&t[p].r<=r)return t[p].data%MOD;
			int ans=0;
			push_down(p);
			if(t[LSON].r>=l)ans=(ans+ask(LSON,l,r))%MOD;
			if(t[RSON].l<=r)ans=(ans+ask(RSON,l,r))%MOD;
			return ans%MOD;
		}
}tree;
//------------------------------------------------------------以上为线段树模板
int ver[MAXN<<1],nxt[MAXN<<1],head[MAXN],tot=1,n,m,r,a[MAXN];
int de[MAXN],fa[MAXN],son[MAXN],siz[MAXN],top[MAXN],dfn[MAXN],fdfn[MAXN],cnt;
void add(int x,int y){
	ver[++tot]=y;
	nxt[tot]=head[x];
	head[x]=tot;
}
void dfs1(int x,int f){
	fa[x]=f,de[x]=de[fa[x]]+1,siz[x]=1;
	for(int i=head[x];i;i=nxt[i]){
		if(ver[i]==fa[x])continue;
		dfs1(ver[i],x);
		siz[x]+=siz[ver[i]];
		if(siz[ver[i]]>siz[son[x]])son[x]=ver[i];
	}
}
void dfs2(int x,int f){
	top[x]=f,dfn[x]=++cnt,fdfn[cnt]=x;
	if(son[x]==0)return;
	dfs2(son[x],f);
	for(int i=head[x];i;i=nxt[i]){
		if(ver[i]==fa[x])continue;
		if(ver[i]==son[x])continue;
		dfs2(ver[i],ver[i]);
	}
}
void x_to_y_add_z(int x,int y,int z){
	while(top[x]!=top[y]){
		if(de[top[x]]<de[top[y]])swap(x,y);
		tree.change(1,dfn[top[x]],dfn[x],z);
		x=fa[top[x]];
	}
	if(de[x]<de[y])swap(x,y);
	tree.change(1,dfn[y],dfn[x],z);
}
int ask_x_to_y(int x,int y){
	int ans=0;
	while(top[x]!=top[y]){
		if(de[top[x]]<de[top[y]])swap(x,y);
		ans=(ans+tree.ask(1,dfn[top[x]],dfn[x]))%MOD;
		x=fa[top[x]];
	}
	if(de[x]<de[y])swap(x,y);
	ans=(ans+tree.ask(1,dfn[y],dfn[x]))%MOD;
	return ans;
}
void x_subtree_add_z(int x,int z){
	tree.change(1,dfn[x],dfn[x]+siz[x]-1,z);
}
int ask_x_subtree(int x){
	return tree.ask(1,dfn[x],dfn[x]+siz[x]-1)%MOD;
}
signed main(){
	scanf("%lld%lld%lld%lld",&n,&m,&r,&MOD);
	for(int i=1,x;i<=n;i++){
		scanf("%lld",&x);
		a[i]=x%MOD;
	}
	for(int i=1,f,t;i<n;i++){
		scanf("%lld%lld",&f,&t);
		add(f,t);
		add(t,f);
	}
	de[r]=1,fa[r]=r;
	dfs1(r,r);dfs2(r,r);
	tree.build(1,1,n,a,fdfn);
	for(int i=1,op,x,y,z;i<=m;i++){
		scanf("%lld",&op);
		if(op==1){
			scanf("%lld%lld%lld",&x,&y,&z);
			x_to_y_add_z(x,y,z%MOD);
		}
		if(op==2){
			scanf("%lld%lld",&x,&y);
			printf("%lld\n",ask_x_to_y(x,y)%MOD);
		}
		if(op==3){
			scanf("%lld%lld",&x,&z);
			x_subtree_add_z(x,z%MOD);
		}
		if(op==4){
			scanf("%lld",&x);
			printf("%lld\n",ask_x_subtree(x)%MOD);
		}
	}
	return 0;
}

细节

要注意线段树实在dfs序上建立的，修改和查询时都要用dfs序。