树状数组学习笔记

树状数组学习笔记

简介

树状数组是一个可以在 \(O(\log n)\) 的时间复杂度内支持单点修改和查询前缀和的操作的数据结构。

原理

观察发现线段树中有很多的冗余的部分。

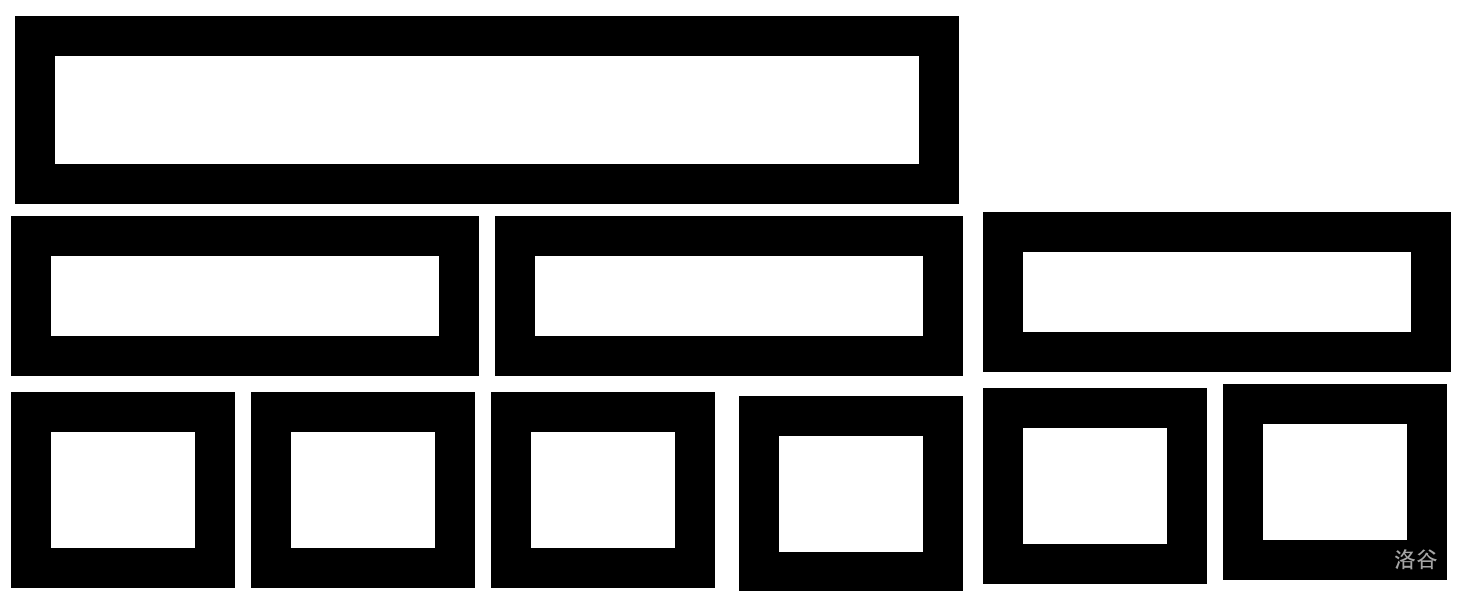
红色部分为冗余部分。

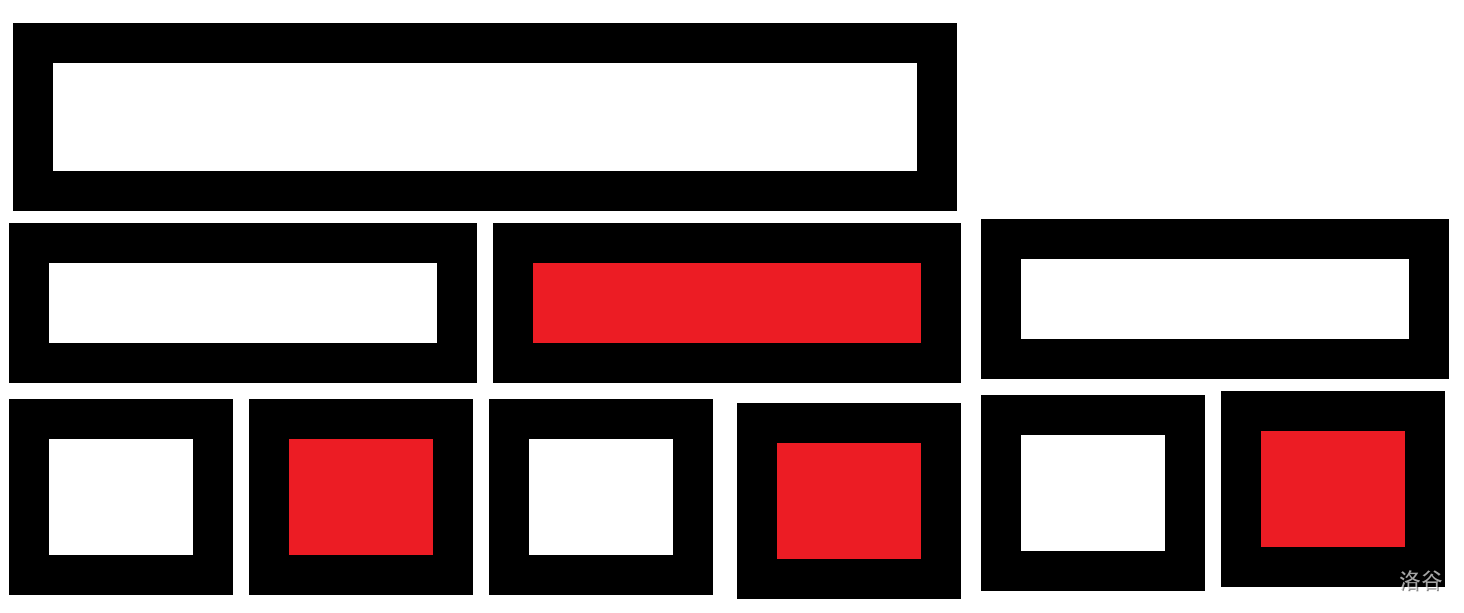
把冗余部分去掉。

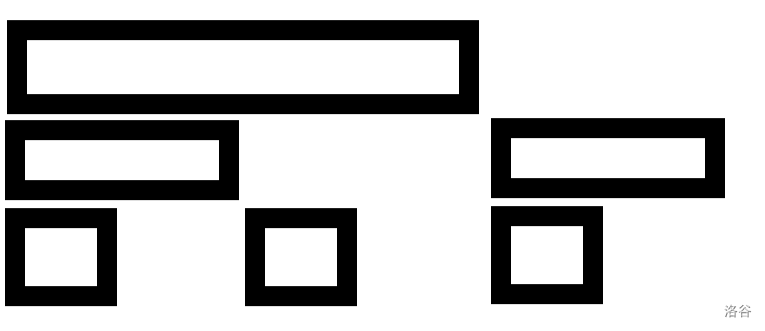
把每个节点编个号。

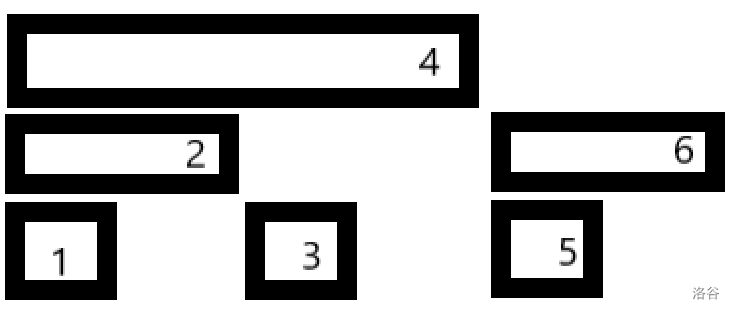
把每个节点的子节点个数和父结点编号列表出来。

1	2	3	4	5	6	7	8
1	2	1	4	1	2	1	8
2	4	4	8	6	8	8	\

这个表有什么规律呢？

\(\text{lowbit}\)

\(\text{lowbit}\) 是指一个数在二进制下最末尾的1的位置。
\(\text{lowbit(x) = x and -x}\)

观察发现，编号为 \(i\) 的节点的子节点个数为 \(\text{lowbit}(i)\)，父结点编号为 \(i+\text{lowbit}(i)\)。

每个点存储和就好了，比如点4存储\([1,4]\)的和，点6存储\([5,6]\)的和。

写法

修改

把点\(i\)的所有祖先节点加上修改的数。

查询

如果要查询\([l,r]\)的和，就可以用\(r\)的前缀和减去\(l-1\)的前缀和。

如何求前缀和呢？

节点 \(i\) 的儿子其实就是 \(i-\text{lowbit}(i)\)，从\(i\)开始往下，一直到儿子为0停止，把中间的节点的和加起来。

比如要求\([1,3]\)，从\(3\)开始，把\([3,3]\)加上，然后跳到\(3-\text{lowbit(3)}=2\)，然后把\([1,2]\)加上，最后跳到\(2-\text{lowbit(2)}=0\)，结束。

具体实现看代码。

代码

int val[MAXN];
void change(int x,int data){//修改&建立
    for(int i=x;i<=MAXN;i+=lowbit(i))val[i]+=data;
}
int ask(int x){//前缀和
    int ans=0;
    for(int i=x;i!=0;i-=lowbit(i))ans+=val[i];
    return ans;
}
int ask(int l,int r){//查询
    return ask(r)-ask(l-1);
}

二维树状数组

可以求出二维数组里的前缀和，时间复杂度\(O(\log^2 n)\)。

与一维树状数组相似。

int val[MAXN][MAXN];
void change(int x,int y,int data){//修改&建立
    for(int i=x;i<=MAXN;i+=lowbit(i))
    for(int j=y;j<=MAXN;j+=lowbit(j))
    val[i][j]+=data;
}
int ask(int x,int y){//前缀和
    int ans=0;
    for(int i=x;i!=0;i-=lowbit(i))
    for(int j=y;j!=0;j-=lowbit(j))    
    ans+=val[i][j];
    return ans;
}
int ask(int x1,int y1,int x2,int y2){//查询
    return ask(x2,y2)-ask(x2,y1-1)-ask(x1-1,y2)+ask(x1-1,y1-1);
}