最近公共祖先(LCA)(RMQ)

【模板】最近公共祖先（LCA）(RMQ)

题目描述

如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

输入格式

第一行包含三个正整数 \(N,M,S\)，分别表示树的结点个数、询问的个数和树根结点的序号。

接下来 \(N-1\) 行每行包含两个正整数 \(x, y\)，表示 \(x\) 结点和 \(y\) 结点之间有一条直接连接的边（数据保证可以构成树）。

接下来 \(M\) 行每行包含两个正整数 \(a, b\)，表示询问 \(a\) 结点和 \(b\) 结点的最近公共祖先。

输出格式

输出包含 \(M\) 行，每行包含一个正整数，依次为每一个询问的结果。

样例 #1

样例输入 #1

5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5

样例输出 #1

4
4
1
4
4

提示

对于 \(30\%\) 的数据，\(N\leq 10\)，\(M\leq 10\)。

对于 \(70\%\) 的数据，\(N\leq 10000\)，\(M\leq 10000\)。

对于 \(100\%\) 的数据，\(N\leq 500000\)，\(M\leq 500000\)。

样例说明：

该树结构如下：

第一次询问：\(2, 4\) 的最近公共祖先，故为 \(4\)。

第二次询问：\(3, 2\) 的最近公共祖先，故为 \(4\)。

第三次询问：\(3, 5\) 的最近公共祖先，故为 \(1\)。

第四次询问：\(1, 2\) 的最近公共祖先，故为 \(4\)。

第五次询问：\(4, 5\) 的最近公共祖先，故为 \(4\)。

故输出依次为 \(4, 4, 1, 4, 4\)。

思路

我们已经学会了\(LCA\)的倍增祖先方法，我们再来学一个时间复杂度更低的算法:\(RMQ\)(\(Range Minimum/Maximum Query\))(区间最值算法)它能解决一个区间内的最值问题。它的预处理时间复杂度为为\(O(nlog_2n)\)查询时间复杂度为\(O(1)\)。它是用\(ST\)表实现的，我在这篇博客里讲过\(ST\)表的模板。但\(RMQ\)是需要一个序列的，而\(LCA\)是树上问题所以我们要把树转换成一个数列。怎么转化呢？

欧拉序

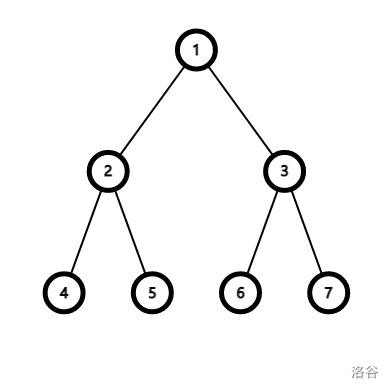
上面这棵树的欧拉序是\(1,2,4,2,5,2,1,3,6,3,7,3,1\)。其实这就是\(dfs\)序的变化，\(dfs\)序是:\(1,2,4,5,3,6,7\)，欧拉序就是每次回溯的时候再把这个节点输出一遍。

初始化

我们已经把一颗树变成了数列，然后就是\(ST\)表的初始化了。
定义:数组\(f[i][j]\)表示第\(i\)个数往后\(2^j\)个数里的深度最小的数，状态转移方程为：

if(de[f[i][j-1]]<de[f[i+2^{j-1}][j-1]])f[i][j]=f[i][j-1]//de[i]表示i的深度
else f[i][j]=f[i+2^{j-1}][j-1]

查询

如果要查\(x\)和\(y\)的最近公共祖先，就现需要查区间\([x,y]\)里的深度最小的数。查询代码：

int l=first[x],r=first[y];//first[i]表示i第一次在欧拉序里出现的位置
if(r<l)swap(l,r);
int k=log2(r-l+1);
return (de[f[l][k]]<de[f[r-(1<<k)+1][k]])?f[l][k]:f[r-(1<<k)+1][k];

完整代码:

提示：数组开大点，欧拉序很长。

#include<cstdio>
#include<cmath>
#define MAXN (5000000+100)
int ver[MAXN*2],next[MAXN*2],head[MAXN*2],bdfs[MAXN*5],de[MAXN],first[MAXN],f[MAXN][100],tot,n,m,s,cnt;
void add(int x,int y){
	ver[++tot]=y;
	next[tot]=head[x];
	head[x]=tot;
}
void swap(int& a,int& b){
	int temp=a;
	a=b;
	b=temp;
}
void dfs(int i,int father,int depth){//dfs求欧拉序和深度
	bdfs[++cnt]=i;
	de[i]=depth;
	if(!first[i])first[i]=cnt;
	for(int j=head[i];j;j=next[j]){
		if(ver[j]!=father){
			dfs(ver[j],i,depth+1);
			bdfs[++cnt]=i;
		}
	}
}
void init_st(){//初始化st表
	for(int i=cnt;i>=1;i--){
		f[i][0]=bdfs[i];
		for(int j=1;j<20;j++){
			if((i+(1<<(j-1)))>cnt){break;}
			f[i][j]=de[f[i][j-1]]<de[f[i+(1<<(j-1))][j-1]]?f[i][j-1]:f[i+(1<<(j-1))][j-1];//状态转移方程
		}
	} 
}
int getlca(int x,int y){//查询
	int l=first[x],r=first[y];
	if(r<l)swap(l,r);
	int k=log2(r-l+1);
	return (de[f[l][k]]<de[f[r-(1<<k)+1][k]])?f[l][k]:f[r-(1<<k)+1][k];
}
int main(){
	scanf("%d%d%d",&n,&m,&s);
	for(int i=1;i<=n-1;i++){
		int u,v;
		scanf("%d%d",&u,&v);
		add(u,v);
		add(v,u);
	}
	dfs(s,0,1);
	init_st();
	for(int i=1;i<=m;i++){
		int x,y;
		scanf("%d%d",&x,&y);
		printf("%d\n",getlca(x,y));
	}
	return 0;
}