最近公共祖先(LCA)(倍增)

【模板】最近公共祖先（LCA）

题目描述

如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

输入格式

第一行包含三个正整数 \(N,M,S\)，分别表示树的结点个数、询问的个数和树根结点的序号。

接下来 \(N-1\) 行每行包含两个正整数 \(x, y\)，表示 \(x\) 结点和 \(y\) 结点之间有一条直接连接的边（数据保证可以构成树）。

接下来 \(M\) 行每行包含两个正整数 \(a, b\)，表示询问 \(a\) 结点和 \(b\) 结点的最近公共祖先。

输出格式

输出包含 \(M\) 行，每行包含一个正整数，依次为每一个询问的结果。

样例 #1

样例输入 #1

5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5

样例输出 #1

4
4
1
4
4

提示

对于 \(30\%\) 的数据，\(N\leq 10\)，\(M\leq 10\)。

对于 \(70\%\) 的数据，\(N\leq 10000\)，\(M\leq 10000\)。

对于 \(100\%\) 的数据，\(N\leq 500000\)，\(M\leq 500000\)。

样例说明：

该树结构如下：

第一次询问：\(2, 4\) 的最近公共祖先，故为 \(4\)。

第二次询问：\(3, 2\) 的最近公共祖先，故为 \(4\)。

第三次询问：\(3, 5\) 的最近公共祖先，故为 \(1\)。

第四次询问：\(1, 2\) 的最近公共祖先，故为 \(4\)。

第五次询问：\(4, 5\) 的最近公共祖先，故为 \(4\)。

故输出依次为 \(4, 4, 1, 4, 4\)。

解题思路

1.暴力思路

很容易想到一个暴力思路：
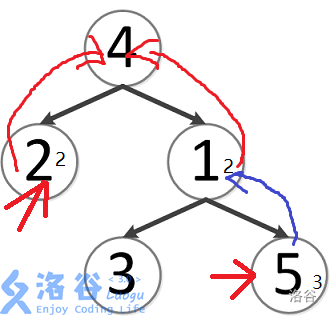
假设要求\(A\)和\(B\)的最近公共祖先,可以先判断\(A\)和\(B\)的深度相不相同，如果一样，就一起一层层地往上跑，直到相遇。如果不一样，就先让深得哪一个跑上来。如图：要求\(5\)和\(2\)的最近公共祖先。发现\(5\)的深度比\(2\)大,\(5\)就先向上跑(蓝线)。它们深度相等后就一起往上跑(红线)，最后发现在\(4\)相遇，因此\(4\)是\(2\)和\(5\)的最近公共祖先。因此我们需要通过\(dfs\)求出\(de\)(深度)数组和\(fa\)(父亲)数组。

暴力代码：

void dfs(int i,int d,int father){
	de[i]=d;//求出de数组
	fa[i]=father;//求出fa数组
	for(int j=head[i];j;j=next[j]){
		if(ver[j]!=father)dfs(ver[j],d+1,i);//dfs
	}
}
int getlca(int x,int y){
	if(x==y)return x;
	while(x!=y){
		if(de[x]==de[y])x=fa[x],y=fa[y];//一起向上跳
		else if(de[x]>de[y])x=fa[x];//如果深度不一样就跳
		else if(de[x]<de[y])y=fa[y];
	}
	return x;
}

2.倍增祖先

暴力思路会有个问题，比如树退化成一条链，就会\(TLE\)。
我们能不能想办法加快跳的速度呢? 我们可以使用倍增的方式加快跳。如：\(8\)，\(4\)，\(2\)，\(1\)，\(0\)。如图:

每次跳到最远能跳的点，这样能大大减少跳的次数。所以我们在\(dfs\)的时候可以多求一个\(f\)数组,\(f_{i,j}\)表示\(i\)的第\(2^j\)个祖先是谁。
转移方程为：\(f[i][j]=f[f[i][j-1]][j-1]\)初始条件为：\(f[i][0]=fa[i]\)(\(i\)的第 \(2^j\) 个祖先\(=\) \(i\) 的第\(2^{j-1}\)个祖先的第\(2^{j-1}\)个祖先。)

倍增代码:

void dfs(int i,int d,int father){
	de[i]=d,f[i][0]=father;//求出de数组
	for(int j=1;j<=log2(d);j++)f[i][j]=f[f[i][j-1]][j-1];//求出f数组
	for(int j=head[i];j;j=next[j]){
		if(ver[j]!=father)dfs(ver[j],d+1,i);//dfs
	}
}
int getlca(int x,int y){
	if(de[x]<de[y])swap(x,y);
	for(int i=19;i>=0;i--){//如果深度不一样就跳
		if(de[f[x][i]]>=de[y])x=f[x][i];
		if(x==y)return x;
	}
	for(int i=19;i>=0;i--){//一起向上跳
		if(f[x][i]!=f[y][i])x=f[x][i],y=f[y][i];
	}
	return f[x][0];
}