Topcoder Srm 671 Div2 1000 BearDestroysDiv2

## $>Topcoder \space Srm \space 671 \space Div2 \space 1000 \space BearDestroysDiv2<$

题目大意 : 有一个 \(W \times H\) 的网格，每一格上有一棵树和一个随机字母 \(S\) 或 \(E\) ，有一只熊在左上角，按从上到下从左到右的顺序遍历每一行每一列，如果其遇到一棵可以推倒的树，就尽可能按照字母表示的方向 (向下，向右) 推倒它，然后其推倒方向的下一棵树就不能被推倒了，同时树不能被推倒在边界之外，求对于所有可能的网格图，树的被推倒个数总和对 \(Mod\) 取模的值 。
\(1 \leq W \leq 7 \ ,1 \leq H \leq 40\)

解题思路 :

观察到 \(W\) 比较小，不妨对列进行状态压缩，又因为直接状压每一列后效性很难讨论，所以维护轮廓线来 \(dp\) 转移.

设 \(f[i][r][j][s]\) 表示第 \(i\) 行维护的轮廓线断点在 \(r\), 轮廓线上的点的状态为 \(s\) ，到目前位置推倒了 \(j\) 棵树的答案

考虑直接将轮廓线上的点定义为 {没推倒，向\(E\)推倒，向\(S\)推倒} 三种不仅无法很好描述状态来转移，复杂度也差强人意

观察发现，对于轮廓线上的点转移到下一状态时，被推倒和因为其他树推倒在它身上导致不能推倒是等价的.

换一种说法，轮廓线上的点对后面状态的更新当且仅当取决于其在此刻能否被推倒，不妨用 \(0\) 表示可以被推倒 \(1\)表示不行

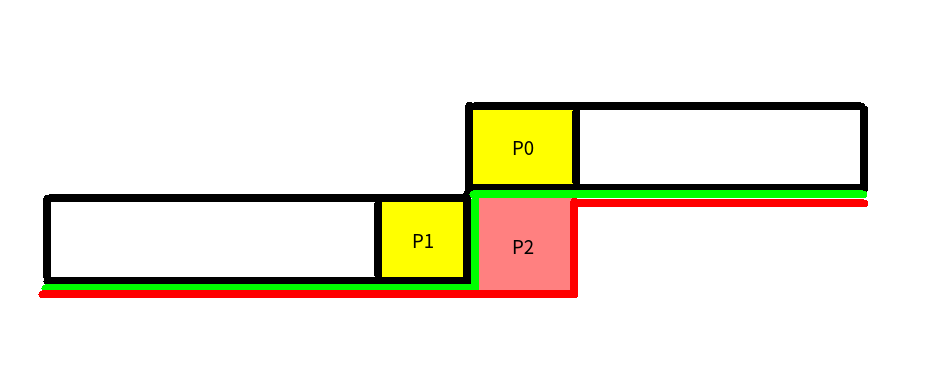
如图所示，绿色的是当前的轮廓线，红色的是要被更新的轮廓线，当前要把点 \(P_2\) 加到轮廓线中.

如果 \(mask(P_0) = 0\) 说明 \(P_0\) 能推倒但因为一些原因没有推倒其右边的点，根据题意，此时 \(P_0\) 必须要向下推倒

考虑 \(P_0\) 被向下推倒了之后，\(P_1\) 就不能向右推倒了，所以 \(P_1\) 如果要向下推倒选 \(S, E\) 都可以.

\(P_2\) 因为被卡住了不能动，所以选 \(S, E\) 也都可以，所以转移的时候方案数的系数为 \(2 \times \max(2 \times [mask(P_1) = 0], 1)\)

如果 \(mask(P_0) = 1\) 且　\(maxk(P_1) = 0\)

此时 \(P_1\) 既可以向下推倒又可以向右推倒，向下的情况只需要保留当且轮廓线的状态即可

考虑 \(P_1\) 要向右推倒，当且仅当 \(P_0\) 没有向下推倒且 \(P_1\) 上的字母为 \(E\) , 所以转移的时候方案数的系数为 \(2\)

如果都不能推倒，那么只需要保留当前轮廓线状态并添加新的点 \(P_2\) 即可

考虑边界的情况，对于所有右边界和下边界，推倒的树的字母都可以选择两种

特别的，对于下边界上的点，\(P_1\) 只能选择向右推倒，对于最后状态产生的未推倒的树，都可以选取两种颜色

所以只需要枚举轮廓线和推倒的树的个数，分类讨论转移

此题细节比较多，建议多算几遍系数，复杂度是 \(O(\frac{W^2H}{2}\times2^W)\)

/*program by mangoyang*/
typedef long long ll;
ll f[45][10][176][1<<7], Mod;
inline void update(ll &x, ll y){ (x += y) %= Mod; }
int BearDestroysDiv2::sumUp(int W, int H, int MOD){
	memset(f, 0, sizeof(f)); 
	int all = W * H / 2 + 1, lim = (1 << W) - 1;
	f[0][W][0][lim] = 1, Mod = MOD;
	for(int i = 1; i <= H; i++){
		for(int j = 0; j <= all; j++)
			for(int s = 0; s <= lim; s++) f[i][0][j][s] = f[i-1][W][j][s];
		for(int r = 0; r < W; r++)
			for(int j = 0; j <= all; j++)
				for(int s = 0; s <= lim; s++){
					if(!((1 << r) & s)){
						ll s2 = (r == W - 1) ? 2 : 1, s1 = 1;
						if(r && !((1 << r - 1) & s) && i != H) s1 = 2; 
						update(f[i][r+1][j+1][s|(1<<r)], f[i][r][j][s] * 2 * s2 * s1);
					}
					else{
						if(i < H) update(f[i][r+1][j][s^(1<<r)], f[i][r][j][s]);
						if(r && !((1 << r - 1) & s)){
							ll s2 = (i == H) ? 2 : 1;
							update(f[i][r+1][j+1][s|(1<<r)|(1<<r-1)], f[i][r][j][s] * 2 * s2);
						}
						else if(i == H) update(f[i][r+1][j][s^(1<<r)], f[i][r][j][s]);
					}
				}	
	}
	ll ans = 0;
	for(int j = 1; j <= all; j++) 
		for(int s = 0; s <= lim; s++) if(f[H][W][j][s]){
			ll res = 1;
			for(int i = 0; i < W; i++)
				if(!((1 << i) & s)) res *= 2;
			update(ans, f[H][W][j][s] * j * res);
		}
	return ans;
}