Codeforces 555 C. Case of Chocolate

\(>Codeforces \space 555 C. Case of Chocolate<\)

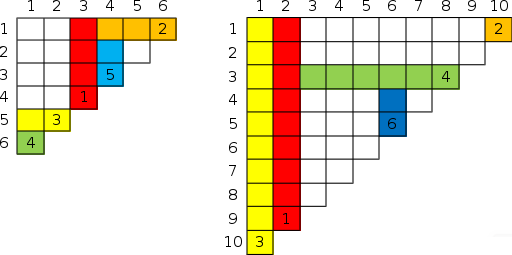
题目大意 : 有一块 \(n \times n\) 的倒三角的巧克力，有一个人要吃 \(q\) 次，每一次从一个在对角线上的点出发，向左或者向上吃若干块，直到吃到已经被吃掉的格子为止，对于每一次吃巧克力的操作，输出这一次被吃掉了多少巧克力。(文字表达不够清晰，可以配合图片理解)

\(1 ≤ n ≤ 10^9\ 1 ≤ q ≤ 2 \times 10^5\)

解题思路 :

询问可以转化为找到某一行或一列第一个被吃掉的位置，那么可以对于每一次修改，用数据结构维护这个东西

离散化后，维护每一行/列被吃掉的编号最大的格子，问题转化为了一个单点询问，区间修改的问题

可以对于行和列各建一棵线段树，对于吃掉行就修改列的线段树，对于吃掉列就修改行的线段树

对于所有询问操作就直接查对应点的答案

对于修改部分，以吃第 \(x\) 行为例，设查询到当前行被吃掉的列编号最大的的编号为 \(y\)

那么对于第 \(y + 1\) 到第 \(n - x + 1\) 列都要对 \(x\) 取 \(max\) 直接区间修改列的线段树即可， 吃列的操作同理

/*program by mangoyang*/
#include<bits/stdc++.h>
#define inf (0x7f7f7f7f)
#define Max(a, b) ((a) > (b) ? (a) : (b))
#define Min(a, b) ((a) < (b) ? (a) : (b))
typedef long long ll;
using namespace std;
template <class T>
inline void read(T &x){
    int f = 0, ch = 0; x = 0;
    for(; !isdigit(ch); ch = getchar()) if(ch == '-') f = 1;
    for(; isdigit(ch); ch = getchar()) x = x * 10 + ch - 48;
    if(f) x = -x;
}
#define lson (u << 1)
#define rson (u << 1 | 1)
#define int ll
#define N (600005)
char t[10];
map<int, int> mp[3];
int s[N], xx[N], yy[N], op[N], ff[N], gg[N], n, q, col;
struct Point{ int x, op, id; } X[N], Y[N];
inline bool cmp(Point A, Point B){ return A.x < B.x; } 
struct SegmentTree{
	int tag[N<<2], mx[N<<2]; 
	inline void pushdown(int u){
		if(!tag[u]) return;
		mx[lson] = Max(mx[lson], tag[u]);
		mx[rson] = Max(mx[rson], tag[u]);
		tag[lson] = Max(tag[lson], tag[u]);
		tag[rson] = Max(tag[rson], tag[u]), tag[u] = 0;
	}
	inline void change(int u, int l, int r, int L, int R, int v){
		if(l >= L && r <= R){
			mx[u] = Max(mx[u], v), tag[u] = Max(tag[u], v); return;
		}
		int mid = l + r >> 1; pushdown(u);
		if(L <= mid) change(lson, l, mid, L, R, v);
		if(mid < R) change(rson, mid + 1, r, L, R, v); 
		mx[u] = Max(mx[lson], mx[rson]);
	}
	inline int query(int u, int l, int r, int pos){
		if(l == r) return mx[u];
		int mid = l + r >> 1; pushdown(u);
		if(pos <= mid) return query(lson, l, mid,  pos);
		else return query(rson, mid + 1, r, pos); 
	}
}R, C;
inline void calcX(int x){ 
	xx[X[x].id] = col, op[X[x].id] = X[x].op, ff[col] = X[x].x; 
}
inline void calcY(int x){ 
	yy[Y[x].id] = col, op[Y[x].id] = Y[x].op, gg[col] = Y[x].x; 
}
main(){
	read(n), read(q);
	for(int i = 1, x, y; i <= q; i++){
		read(x), read(y), scanf("%s", t);
		if(t[0] == 'U') X[i] = (Point){x, 1, i}, Y[i] = (Point){y, 1, i};
		if(t[0] == 'L') X[i] = (Point){x, 2, i}, Y[i] = (Point){y, 2, i}; 
	}
	sort(X + 1, X + q + 1, cmp), ++col, calcX(1);
	for(int i = 2; i <= q; i++){ if(X[i].x > X[i-1].x) ++col; calcX(i); }
	int m = col; col = 0;
	sort(Y + 1, Y + q + 1, cmp), ++col, calcY(1);
	for(int i = 2; i <= q; i++){ if(Y[i].x > Y[i-1].x) ++col; calcY(i); }
	m = max(m, col) + 100000;
	for(int i = 1; i <= q; i++){
		if(op[i] == 1){
			if(mp[1][xx[i]]){ puts("0"); continue; }
			int ls = R.query(1, 1, m, xx[i]); mp[1][xx[i]] = 1;
			C.change(1, 1, m, ls + 1, yy[i], xx[i]);
			printf("%lld\n", n - ff[xx[i]] + 1 - gg[ls]);
		}
		if(op[i] == 2){
			if(mp[2][yy[i]]){ puts("0"); continue; }
			int ls = C.query(1, 1, m, yy[i]); mp[2][yy[i]] = 1;
			R.change(1, 1, m, ls + 1, xx[i], yy[i]);
			printf("%lld\n", n - gg[yy[i]] + 1 - ff[ls]);
		}
	}
	return 0;
}