Atcoder Grand Contest 018 E - Sightseeing Plan

Atcoder Grand Contest 018 E - Sightseeing Plan

枚举从第二个矩形的 \((x_1,y_1)\) 进入，\((x_2,y_2)\) 出来，那么中间可以选的点的数量是 \(x_2+y_2-x_1-x_2+1\) ，也就是说对于每一条合法路线，从 \((x_1,y_1)\) 进入的贡献为 \(-x_1-x_2\) ，从 \((x_2,y_2)\) 出来的贡献为 \(x_2+y_2+1\) ，枚举一下第二个矩形边界上的点，我们只需要分别计算某个点到第一个矩形的方案数和到第三个矩形的方案数即可。

考虑一个点到一个矩形的方案数是有一个组合意义转化的。

记 \(F(x,y)\) 表示 \((0,0)\) 到 \((x, y)\) 的方案数，有以下结论：

\[\sum_{i=0}^yF(x,i) =F(x,y+1) \\ \sum_{i=0}^x\sum_{j=0}^y F(i,j)=F(x+1,y+1)-1 \]

组合意义证明的话如图：

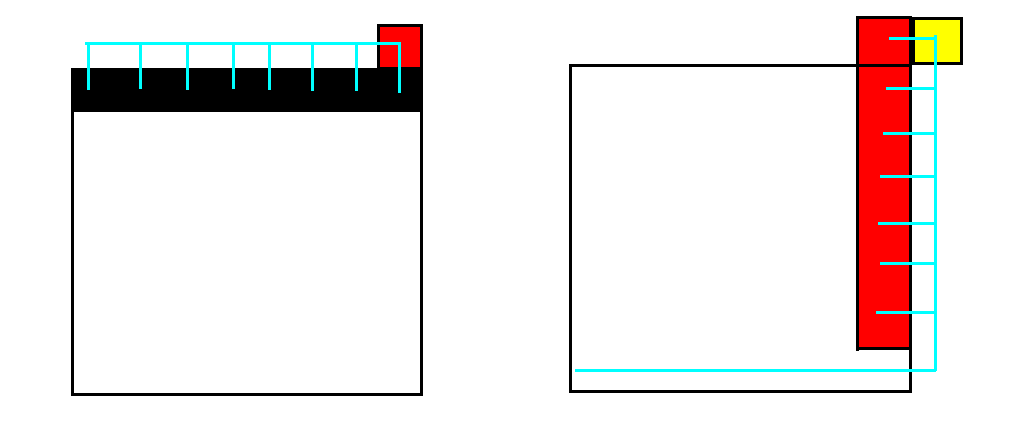
考虑第一个式子就相当于 \((0,0)\) 到左边这一排黑点的方案数，那么考虑到这个红点的每一种方案，因为每一条路径穿过第一个黑点以后的方案数唯一，第一个式子正确性显然。

第二个式子就相当于每一排的和，由第一个式子转化后就相当于要求右边这一排红点的方案数，先补上最下面一个红点，然后方案数就是到达黄点的方案数，最后再减去去掉经过最后一个红点的方案数 \(1\) 就是第二个式子

实际上写成组合数的性质利用一些经典恒等式也可以证明，但这里用组合意义更有趣一点。

code

/*program by mangoyang*/
#include <bits/stdc++.h>
#define inf (0x7f7f7f7f)
#define Max(a, b) ((a) > (b) ? (a) : (b))
#define Min(a, b) ((a) < (b) ? (a) : (b))
typedef long long ll;
using namespace std;
template <class T>
inline void read(T &x){
	int ch = 0, f = 0; x = 0;
	for(; !isdigit(ch); ch = getchar()) if(ch == '-') f = 1;
	for(; isdigit(ch); ch = getchar()) x = x * 10 + ch - 48;
	if(f) x = -x;
}
const int N = 2000005, mod = 1e9 + 7;
int js[N], inv[N], X[7], Y[7], ans;
inline void up(int &x, int y){ 
	x = x + y >= mod ? x + y - mod : x + y; 
}
inline int Pow(int a, int b){
	int ans = 1;
	for(; b; b >>= 1, a = 1ll * a * a % mod)
		if(b & 1) ans = 1ll * ans * a % mod;
	return ans;
}
inline int C(int x, int y){
	return 1ll * js[x] * inv[y] % mod * inv[x-y] % mod;
}
inline int GAO(int X1, int Y1, int X2, int Y2){
	int res = 0;
	up(res, C(X2 + Y2 + 2, Y2 + 1));
	up(res, C(X1 + Y1, Y1));
	up(res, mod - C(X2 + Y1 + 1, X2 + 1));
	up(res, mod - C(Y2 + X1 + 1, Y2 + 1));
	return res;
}

inline int gao1(int x, int y){
	return 1ll * GAO(x - X[2], y - Y[2] - 1, x - X[1], y - Y[1] - 1)
		* GAO(X[5] - x, Y[5] - y, X[6] - x, Y[6] - y) % mod;
}
inline int gao2(int x, int y){
	return 1ll * GAO(x - X[2], y - Y[2], x - X[1], y - Y[1])
		* GAO(X[5] - x, Y[5] - y - 1, X[6] - x, Y[6] - y - 1) % mod;
}
inline int gao3(int x, int y){
	return 1ll * GAO(x - X[2] - 1, y - Y[2], x - X[1] - 1, y - Y[1])
		* GAO(X[5] - x, Y[5] - y, X[6] - x, Y[6] - y) % mod;
}
inline int gao4(int x, int y){
	return 1ll * GAO(x - X[2], y - Y[2], x - X[1], y - Y[1])
		* GAO(X[5] - x - 1, Y[5] - y, X[6] - x - 1, Y[6] - y) % mod;
}
int main(){
	js[0] = inv[0] = 1;
	for(int i = 1; i < N; i++){
		js[i] = 1ll * js[i-1] * i % mod;
		inv[i] = Pow(js[i], mod - 2);
	}
	for(int i = 1; i <= 6; i++) read(X[i]);
	for(int i = 1; i <= 6; i++) read(Y[i]);
	for(int i = X[3]; i <= X[4]; i++){
		up(ans, 1ll * gao1(i, Y[3]) * (mod - i - Y[3]) % mod);
		up(ans, 1ll * gao2(i, Y[4]) * (i + Y[4] + 1) % mod);
	}
	for(int i = Y[3]; i <= Y[4]; i++){
		up(ans, 1ll * gao3(X[3], i) * (mod - X[3] - i) % mod);
		up(ans, 1ll * gao4(X[4], i) * (X[4] + i + 1) % mod);
	}
	cout << ans << endl;
	return 0;
}