树链剖分
树链剖分是把一棵树分割成若干条链,以进行树上操作的一种方法。树链剖分有很多种类,本文主要介绍最常用的重链剖分。
重链剖分
一、定义
一个节点的子节点中子树大小最大的为重子节点,其余节点为轻子节点。特别地,若有多个子节点的子树大小相等,则在其中任选一个作为重子节点,其余为轻子节点。
一个节点到其重子节点的边为重边,到轻子节点的边为轻边。
假设根节点是轻节点,那么我们从每个轻节点开始一直往下走重边,则每一条路都对应了一条链。
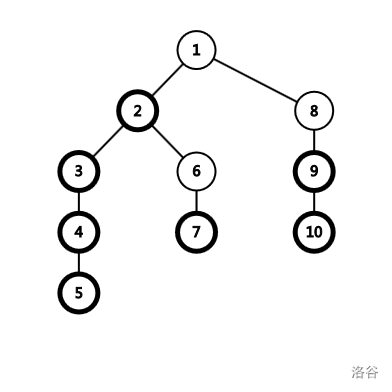
二、实现
我们 \(\rm dfs\) 两次来剖分。\(\operatorname{dfs1}\) 求出每个节点的 \(fa\)(父节点)、\(dep\)(深度)、\(siz\)(子树大小)、\(son\)(重子节点)。\(\operatorname{dfs2}\) 求出 \(dfn\)(dfs 序)、\(top\)(链头)。
int Time;
int fa[MAXN], dep[MAXN], siz[MAXN], son[MAXN], dfn[MAXN], top[MAXN];
void dfs1(int u, int father)
{
fa[u] = father;
dep[u] = dep[father] + 1;
siz[u] = 1;
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].to;
if (v == father)
{
continue;
}
dfs1(v, u);
siz[u] += siz[v];
if (siz[v] > siz[son[u]])
{
son[u] = v;
}
}
}
void dfs2(int u, int topp)
{
dfn[u] = ++Time;
top[u] = topp;
if (son[u])
{
dfs2(son[u], topp); // heavy_son's top is u's top
}
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].to;
if (top[v]) // v is u's father or u's heavy_son
{
continue;
}
dfs2(v, v); // v's top is itself
}
}
剖分之后,一棵树变成了若干条链(可看做序列)且有以下性质:
1. 一条链上的所有节点的 \(dfn\) 是连续的。
2. 一个节点的子树中所有节点的 \(dfn\) 也是连续的。
利用以上性质,我们就可以进行许多神奇的操作了。
三、操作
1.求 LCA
之前我们用倍增算法求过 \(\operatorname{LCA(x,y)}\),现在我们用树链剖分也可以求。
若 \(x\) 和 \(y\) 在同一条链上,那么 \(LCA\) 就是深度小的那个节点。
否则,\(LCA\) 要么在链头深度小的链上,要么是两个链头的父节点的 \(LCA\),但不可能在链头深度大的链上。
证明:
不妨设 \(dep[top[x]]\le dep[top[y]]\),且 \(LCA\) 在 \(y\) 所在的链上。
则 \(dep[LCA]\ge dep[top[y]]\),故 \(dep[LCA]\ge dep[top[x]]\)。
\(top[x]\) 是 \(x\) 的祖先,\(LCA\) 也是 \(x\) 的祖先,则 \(LCA\) 在 \(x\) 所在的链上,矛盾。
所以可以直接把链头深度较大的节点换成链头的父节点,然后继续求父节点与另一节点的 \(LCA\)。
int lca(int x, int y)
{
while (top[x] != top[y])
{
if (dep[top[x]] < dep[top[y]])
{
swap(x, y);
}
x = fa[top[x]];
}
if (dep[x] > dep[y])
{
swap(x, y);
}
return x;
}
2. 链上操作 + 子树操作
操作 \(1\):将树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值都加上 \(z\)。
类似求 \(\rm LCA\) 的过程,不妨设 \(dep(top(x))\ge dep(top(y))\),根据性质 \(1\),每次 \(\operatorname{update(1,dfn(top(x)),dfn(x),z)}\),并令 \(x\gets fa(top(x))\)。当 \(top(x)=top(y)\) 时,不妨设 \(dep(x)\le dep(y)\),\(\operatorname{update(1,dfn(x),dfn(y))}\)。
void update_path(int x, int y, int z)
{
while (top[x] != top[y])
{
if (dep[top[x]] < dep[top[y]])
{
swap(x, y);
}
update(1, dfn[top[x]], dfn[x], z);
x = fa[top[x]];
}
if (dep[x] > dep[y])
{
swap(x, y);
}
update(1, dfn[x], dfn[y], z);
}
操作 \(2\):求树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值之和。
同操作 \(1\),不妨设 \(dep(top(x))\ge dep(top(y))\),每次令 \(res\gets res+\operatorname{query(1,dfn(top(x)),dfn(x))}\),并令 \(x\gets fa(top(x))\)。当 \(top(x)=top(y)\) 时,不妨设 \(dep(x)\le dep(y)\),令 \(res\gets res+\operatorname{query(1,dfn(x),dfn(y))}\)。
int query_path(int x, int y)
{
int res = 0;
while (top[x] != top[y])
{
if (dep[top[x]] < dep[top[y]])
{
swap(x, y);
}
res += query(1, dfn[top[x]], dfn[x]);
x = fa[top[x]];
}
if (dep[x] > dep[y])
{
swap(x, y);
}
res += query(1, dfn[x], dfn[y]);
return res;
}
操作 \(3\):将以 \(x\) 为根节点的子树内所有节点值都加上 \(z\)。
根据性质 \(2\),子树内 \(dfn\) 最小的是 \(dfn(x)\),子树内共 \(siz(x)\) 的节点,故 \(dfn\) 最大的是 \(dfn(x)+siz(x)-1\)。直接 \(\operatorname{update(1,dfn(x),dfn(x)+siz(x)-1,z)}\) 即可。
void update_subtree(int x, int z)
{
update(1, dfn[x], dfn[x] + siz[x] - 1, z);
}
操作 \(4\):求以 \(x\) 为根节点的子树内所有节点值之和。
同操作 \(3\),\(res=\operatorname{query(1,dfn(x),dfn(x)+siz(x)-1)}\)。
int query_subtree(int x)
{
return query(1, dfn[x], dfn[x] + siz[x] - 1);
}
需要注意的是,以上 \(\operatorname{update}\) 和 \(\operatorname{query}\) 函数的参数 \(L,R\) 均为 \(dfn\),因此在 \(\operatorname{dfs2}\) 时需要把读入的数改按 \(dfn\) 存。
void dfs2(int u, int topp)
{
dfn[u] = ++Time;
a[Time] = b[u]; //b为读入的,a为按dfn存的
top[u] = topp;
if (son[u])
{
dfs2(son[u], topp);
}
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].to;
if (top[v])
{
continue;
}
dfs2(v, v);
}
}
其中的 \(\operatorname{update}\) 和 \(\operatorname{query}\) 函数为区修区查,可用线段树或树状数组实现(您甚至可以尝试分块)。
Code
#include <iostream>
#include <cstdio>
using namespace std;
const int MAXN = 1e5 + 5;
int n, m, r, p, cnt, Time;
int a[MAXN], b[MAXN], head[MAXN], fa[MAXN], dep[MAXN], siz[MAXN], son[MAXN], top[MAXN], dfn[MAXN];
struct edge
{
int to, nxt;
}e[MAXN << 1];
void add(int u, int v)
{
e[++cnt] = edge{v, head[u]};
head[u] = cnt;
}
void dfs1(int u, int father)
{
dep[u] = dep[father] + 1;
fa[u] = father;
siz[u] = 1;
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].to;
if (v == father)
{
continue;
}
dfs1(v, u);
siz[u] += siz[v];
if (siz[v] > siz[son[u]])
{
son[u] = v;
}
}
}
void dfs2(int u, int topp)
{
dfn[u] = ++Time;
a[Time] = b[u];
top[u] = topp;
if (son[u])
{
dfs2(son[u], topp);
}
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].to;
if (top[v])
{
continue;
}
dfs2(v, v);
}
}
#define lson pos << 1
#define rson pos << 1 | 1
struct tree
{
int l, r, val, siz, tag;
}t[MAXN << 2];
void pushup(int pos)
{
t[pos].val = (t[lson].val + t[rson].val) % p;
}
void pushdown(int pos)
{
if (t[pos].tag)
{
t[lson].val = (t[lson].val + t[pos].tag * t[lson].siz) % p;
t[lson].tag = (t[lson].tag + t[pos].tag) % p;
t[rson].val = (t[rson].val + t[pos].tag * t[rson].siz) % p;
t[rson].tag = (t[rson].tag + t[pos].tag) % p;
t[pos].tag = 0;
}
}
void build(int pos, int l, int r)
{
t[pos].l = l, t[pos].r = r, t[pos].siz = r - l + 1;
if (l == r)
{
t[pos].val = a[l] % p;
return;
}
int mid = (l + r) >> 1;
build(lson, l, mid);
build(rson, mid + 1, r);
pushup(pos);
}
void update(int pos, int L, int R, int k)
{
int l = t[pos].l, r = t[pos].r;
if (l >= L && r <= R)
{
t[pos].val = (t[pos].val + t[pos].siz * k) % p;
t[pos].tag = (t[pos].tag + k) % p;
return;
}
pushdown(pos);
int mid = (l + r) >> 1;
if (L <= mid)
{
update(lson, L, R, k);
}
if (R > mid)
{
update(rson, L, R, k);
}
pushup(pos);
}
int query(int pos, int L, int R)
{
int l = t[pos].l, r = t[pos].r;
if (l >= L && r <= R)
{
return t[pos].val;
}
pushdown(pos);
int mid = (l + r) >> 1, res = 0;
if (L <= mid)
{
res = query(lson, L, R) % p;
}
if (R > mid)
{
res = (res + query(rson, L, R)) % p;
}
return res;
}
void update_path(int x, int y, int z)
{
while (top[x] != top[y])
{
if (dep[top[x]] < dep[top[y]])
{
swap(x, y);
}
update(1, dfn[top[x]], dfn[x], z);
x = fa[top[x]];
}
if (dep[x] > dep[y])
{
swap(x, y);
}
update(1, dfn[x], dfn[y], z);
}
int query_path(int x, int y)
{
int res = 0;
while (top[x] != top[y])
{
if (dep[top[x]] < dep[top[y]])
{
swap(x, y);
}
res = (res + query(1, dfn[top[x]], dfn[x])) % p;
x = fa[top[x]];
}
if (dep[x] > dep[y])
{
swap(x, y);
}
res = (res + query(1, dfn[x], dfn[y])) % p;
return res;
}
void update_subtree(int x, int z)
{
update(1, dfn[x], dfn[x] + siz[x] - 1, z);
}
int query_subtree(int x)
{
return query(1, dfn[x], dfn[x] + siz[x] - 1);
}
int main()
{
scanf("%d%d%d%d", &n, &m, &r, &p);
for (int i = 1; i <= n; i++)
{
scanf("%d", b + i);
}
for (int i = 1; i < n; i++)
{
int x, y;
scanf("%d%d", &x, &y);
add(x, y);
add(y, x);
}
dfs1(r, 0);
dfs2(r, r);
build(1, 1, n);
while (m--)
{
int op, x, y, z;
scanf("%d%d", &op, &x);
if (op == 1)
{
scanf("%d%d", &y, &z);
update_path(x, y, z % p);
}
else if (op == 2)
{
scanf("%d", &y);
printf("%d\n", query_path(x, y));
}
else if (op == 3)
{
scanf("%d", &z);
update_subtree(x, z % p);
}
else
{
printf("%d\n", query_subtree(x));
}
}
return 0;
}
四、时间复杂度
预处理:\(2\) 次 dfs 时间均为 \(\operatorname{O}(n)\),线段树 \(\operatorname{build}\) 时间为 \(\operatorname{O}(n)\)。
操作:线段树每次 \(\operatorname{update}\) 和 \(\operatorname{query}\) 时间为 \(\operatorname{O}(\log n)\),跳链最多 \(\log n\) 次,故每次操作时间为 \(\operatorname{O}(\log^2n)\)。
综上,树链剖分的时间复杂度为 \(\operatorname{O}(n+q\log^2n)\)

