换根树剖
P3979 遥远的国度
本题需要支持 \(3\) 个操作:
- 把根修改为 \(id\);
- 将 \(x\;y\) 路径上的所有点权修改为 \(v\);
- 询问以 \(x\) 为根的子树中的最小点权。
看到这道题,第一思路就是对于每个操作 \(1\),换根后重新剖一遍。但时间复杂度为 \(\operatorname{O}(qn)\)!直接原地爆炸
所以,我们想到另一种方法,直接以 \(1\) 为根来剖,记录当前的根,每次修改和查询的时候再根据根的位置回答。
对于修改操作,由于一棵树上任意两点间只有一条路径,所以直接修改就行了。
重点是查询:
设当前的根为 \(rt\),要询问以 \(x\) 为根的子树中的最小值。
- \(x=rt\):直接输出全局最小值;
- \(rt\) 是 \(x\) 的祖先:直接输出 \(x\) 的子树的最小值;
- \(x\) 是 \(rt\) 的祖先:这种情况非常\(\color{White}{毒瘤}\)有意思!我们待会会讨论如何处理;
- 以上情况都不是,相当于 \(x\) 在其他的分支,也是直接输出 \(x\) 的子树的最小值。
判断顺序:先判断是否是 \(1\),再判断是否是 \(3\),剩下自然就是 \(2\) 和 \(4\) 了。
现在讨论一下如何处理情况 \(3\):
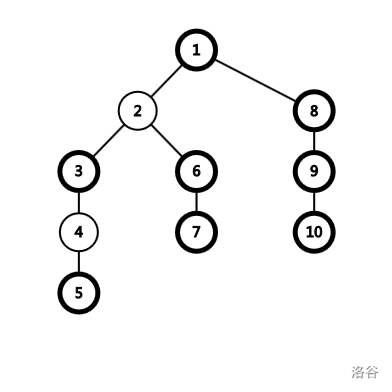
如图,若 \(x=2,rt=4\),则以 \(4\) 为根时,\(2\) 的子树就是除了往 \(4\) 的方向的节点外的所有节点。也就是要找 \(x\) 到 \(rt\) 这条路径上 \(x\) 的儿子。
找的方法可以用倍增,记录 \(fa(x)(i)\) 为 \(x\) 的第 \(2^i\) 级祖先,\(\operatorname{getfa}(x,k)\) 函数返回 \(x\) 的第 \(k\) 级祖先,实现如下:
int getfa(int x, int k)
{
for (int i = lg[k]; i >= 0; i--)
{
if (k >= (1 << i))
{
x = fa[x][i];
k -= (1 << i);
}
}
return x;
}
令 \(y\gets\operatorname{getfa}(x,dep[rt]-dep[x]-1)\),我们只需判断 \(fa(y)(0)\) 是否等于 \(x\) 即可,这样既判断了 \(x\) 是否是 \(rt\) 的祖先,又顺便求出了 \(y\)。
\(\Large\text{Code}\)
#include <iostream>
#include <cstdio>
using namespace std;
const int MAXN = 1e5 + 5;
const int INF = 0x7fffffff;
int cnt, Time;
int b[MAXN], a[MAXN], head[MAXN], fa[MAXN][18], lg[MAXN], dep[MAXN], siz[MAXN], son[MAXN], dfn[MAXN], top[MAXN];
struct edge
{
int to, nxt;
}e[MAXN << 1];
void add(int u, int v)
{
e[++cnt] = edge{v, head[u]};
head[u] = cnt;
}
void dfs1(int u, int father)
{
fa[u][0] = father;
for (int i = 1; i <= 17; i++)
{
fa[u][i] = fa[fa[u][i - 1]][i - 1];
}
dep[u] = dep[father] + 1;
siz[u] = 1;
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].to;
if (v == father)
{
continue;
}
dfs1(v, u);
siz[u] += siz[v];
if (siz[v] > siz[son[u]])
{
son[u] = v;
}
}
}
void dfs2(int u, int topp)
{
dfn[u] = ++Time;
a[Time] = b[u];
top[u] = topp;
if (son[u])
{
dfs2(son[u], topp);
}
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].to;
if (top[v])
{
continue;
}
dfs2(v, v);
}
}
int getfa(int x, int k)
{
for (int i = lg[k]; i >= 0; i--)
{
if (k >= (1 << i))
{
x = fa[x][i];
k -= (1 << i);
}
}
return x;
}
#define lson pos << 1
#define rson pos << 1 | 1
struct tree
{
int l, r, val = INF, tag;
}t[MAXN << 2];
void pushup(int pos)
{
t[pos].val = min(t[lson].val, t[rson].val);
}
void pushdown(int pos)
{
if (t[pos].tag)
{
t[lson].val = t[lson].tag = t[rson].val = t[rson].tag = t[pos].tag;
t[pos].tag = 0;
}
}
void build(int pos, int l, int r)
{
t[pos].l = l, t[pos].r = r;
if (l == r)
{
t[pos].val = a[l];
return;
}
int mid = (l + r) >> 1;
build(lson, l, mid);
build(rson, mid + 1, r);
pushup(pos);
}
void update(int pos, int L, int R, int k)
{
int l = t[pos].l, r = t[pos].r;
if (l >= L && r <= R)
{
t[pos].val = t[pos].tag = k;
return;
}
pushdown(pos);
int mid = (l + r) >> 1;
if (L <= mid)
{
update(lson, L, R, k);
}
if (R > mid)
{
update(rson, L, R, k);
}
pushup(pos);
}
int query(int pos, int L, int R)
{
int l = t[pos].l, r = t[pos].r;
if (l >= L && r <= R)
{
return t[pos].val;
}
pushdown(pos);
int mid = (l + r) >> 1, res = INF;
if (L <= mid)
{
res = query(lson, L, R);
}
if (R > mid)
{
res = min(res, query(rson, L, R));
}
return res;
}
void update_path(int x, int y, int v)
{
while (top[x] != top[y])
{
if (dep[top[x]] < dep[top[y]])
{
swap(x, y);
}
update(1, dfn[top[x]], dfn[x], v);
x = fa[top[x]][0];
}
if (dep[x] < dep[y])
{
swap(x, y);
}
update(1, dfn[y], dfn[x], v);
}
int query_subtree(int x)
{
return query(1, dfn[x], dfn[x] + siz[x] - 1);
}
int main()
{
int n, m, u, v, rt, op, x, y;
scanf("%d%d", &n, &m);
for (int i = 2; i <= n; i++)
{
lg[i] = lg[i >> 1] + 1;
}
for (int i = 1; i < n; i++)
{
scanf("%d%d", &u, &v);
add(u, v);
add(v, u);
}
for (int i = 1; i <= n; i++)
{
scanf("%d", b + i);
}
dfs1(1, 0);
dfs2(1, 1);
build(1, 1, n);
scanf("%d", &rt);
while (m--)
{
scanf("%d", &op);
if (op == 1)
{
scanf("%d", &rt);
}
else if (op == 2)
{
scanf("%d%d%d", &x, &y, &v);
update_path(x, y, v);
}
else
{
scanf("%d", &x);
if (x == rt)
{
printf("%d\n", t[1].val);
}
else if (dep[x] < dep[rt] && fa[y = getfa(rt, dep[rt] - dep[x] - 1)][0] == x)
{
if (dfn[y] + siz[y] <= n)
{
printf("%d\n", min(query(1, 1, dfn[y] - 1), query(1, dfn[y] + siz[y], n)));
}
else
{
printf("%d\n", query(1, 1, dfn[y] - 1));
}
}
else
{
printf("%d\n", query_subtree(x));
}
}
}
return 0;
}
CF916E Jamie and Tree
- 给定一个点 \(v\),将整颗树的根变为 \(v\);
- 给定两个点 \(u, v\),将 \(lca(u, v)\) 所在的子树都加上 \(x\);
- 给定一个点 \(v\),回答以 \(v\) 所在的子树的权值和。
这道题的操作 \(1\) 和 \(3\) 都和上一题一样,只是操作 \(2\) 变成了子树修改,所以也要分类讨论:
- \(lca=rt\):直接将全局和加上 \(x\);
- \(lca\) 是 \(rt\) 的祖先:同查询,记 \(lca\) 到 \(rt\) 这条路径上 \(lca\) 的儿子为 \(son\),我们可以先将全局和加上 \(x\),再将 \(son\) 的子树和减去 \(x\),这样相当于 \(son\) 的子树都没加。
- 其他情况下直接将 \(lca\) 的子树和加 \(x\)。
但是还有一个坑,就是 \(lca\) 也会根据 \(rt\) 的位置而改变!
- \(u\) 和 \(v\) 都在 \(rt\) 的子树内:\(lca\gets\operatorname{LCA}(u,v)\);
- 其中一个在 \(rt\) 的子树内:\(lca\gets rt\);
- \(u\) 和 \(v\) 都不在 \(rt\) 的子树内:\(lca\) 为 \(\operatorname{LCA}(u,rt)\) 和 \(\operatorname{LCA}(v,rt)\) 中深度较大的。
综上,可以发现,以上 \(3\) 种情况的 \(lca\) 都满足是 \(\operatorname{LCA}(u,v),\operatorname{LCA}(u,rt)\) 和 \(\operatorname{LCA}(v,rt)\) 中深度最大的那个。
\(\Large\text{Code}\)
#include <iostream>
#include <cstdio>
#define int long long
#define re register
using namespace std;
inline int read()
{
re int x = 0, f = 0;
re char c = getchar();
while (c < '0' || c > '9')
{
f |= c == '-';
c = getchar();
}
while (c >= '0' && c <= '9')
{
x = (x << 3) + (x << 1) + (c ^ 48);
c = getchar();
}
return f ? -x : x;
}
inline void write(int x)
{
if (x < 0)
{
putchar('-');
x = -x;
}
if (x > 9)
{
write(x / 10);
}
putchar(x % 10 ^ '0');
}
inline void swap2(int &x, int &y)
{
x ^= y ^= x ^= y;
}
inline int min2(int x, int y)
{
return x < y ? x : y;
}
//--------------------------------------------
const int MAXN = 1e5 + 5;
int cnt, Time;
int a[MAXN], b[MAXN], head[MAXN], fa[MAXN][18], lg[MAXN], dep[MAXN], siz[MAXN], son[MAXN], dfn[MAXN], top[MAXN];
struct edge
{
int to, nxt;
}e[MAXN << 1];
void add(int u, int v)
{
e[++cnt] = edge{v, head[u]};
head[u] = cnt;
}
void dfs1(int u, int father)
{
fa[u][0] = father;
dep[u] = dep[father] + 1;
siz[u] = 1;
for (re int i = 1; i <= 17; i++)
{
fa[u][i] = fa[fa[u][i - 1]][i - 1];
}
for (re int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].to;
if (v == father)
{
continue;
}
dfs1(v, u);
siz[u] += siz[v];
if (siz[v] > siz[son[u]])
{
son[u] = v;
}
}
}
void dfs2(int u, int topp)
{
dfn[u] = ++Time;
a[Time] = b[u];
top[u] = topp;
if (son[u])
{
dfs2(son[u], topp);
}
for (re int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].to;
if (top[v])
{
continue;
}
dfs2(v, v);
}
}
int lca(int x, int y)
{
if (dep[x] < dep[y])
{
swap2(x, y);
}
while (dep[x] > dep[y])
{
x = fa[x][lg[dep[x] - dep[y]]];
}
if (x == y)
{
return x;
}
for (re int i = 17; i >= 0; i--)
{
if (fa[x][i] != fa[y][i])
{
x = fa[x][i];
y = fa[y][i];
}
}
return fa[x][0];
}
int getfa(int x, int k)
{
for (re int i = lg[k]; i >= 0; i--)
{
if (k >= (1 << i))
{
x = fa[x][i];
k -= (1 << i);
}
}
return x;
}
#define lson pos << 1
#define rson pos << 1 | 1
struct tree
{
int l, r, siz, val, tag;
}t[MAXN << 2];
void pushup(int pos)
{
t[pos].val = t[lson].val + t[rson].val;
}
void cal(int pos, int val)
{
t[pos].val += val * t[pos].siz;
t[pos].tag += val;
}
void pushdown(int pos)
{
if (t[pos].tag)
{
cal(lson, t[pos].tag);
cal(rson, t[pos].tag);
t[pos].tag = 0;
}
}
void build(int pos, int l, int r)
{
t[pos].l = l, t[pos].r = r, t[pos].siz = r - l + 1;
if (l == r)
{
t[pos].val = a[l];
return;
}
int mid = (l + r) >> 1;
build(lson, l, mid);
build(rson, mid + 1, r);
pushup(pos);
}
void update(int pos, int L, int R, int k)
{
int l = t[pos].l, r = t[pos].r;
if (L <= l && r <= R)
{
cal(pos, k);
return;
}
pushdown(pos);
int mid = (l + r) >> 1;
if (L <= mid)
{
update(lson, L, R, k);
}
if (R > mid)
{
update(rson, L, R, k);
}
pushup(pos);
}
int query(int pos, int L, int R)
{
int l = t[pos].l, r = t[pos].r;
if (L <= l && r <= R)
{
return t[pos].val;
}
pushdown(pos);
int mid = (l + r) >> 1, res = 0;
if (L <= mid)
{
res = query(lson, L, R);
}
if (R > mid)
{
res += query(rson, L, R);
}
return res;
}
void update_subtree(int x, int k)
{
update(1, dfn[x], dfn[x] + siz[x] - 1, k);
}
int query_subtree(int x)
{
return query(1, dfn[x], dfn[x] + siz[x] - 1);
}
int getlca(int x, int y, int z) //3个lca中深度最大的
{
int a = lca(x, y), b = lca(x, z), c = lca(y, z);
if (dep[a] < dep[b])
{
a = b;
}
if (dep[a] < dep[c])
{
a = c;
}
return a;
}
signed main()
{
int n = read(), q = read(), rt = 1;
for (re int i = 2; i <= n; i++)
{
lg[i] = lg[i >> 1] + 1;
}
for (re int i = 1; i <= n; i++)
{
b[i] = read();
}
for (re int i = 1; i < n; i++)
{
int u = read(), v = read();
add(u, v);
add(v, u);
}
dfs1(1, 0);
dfs2(1, 1);
build(1, 1, n);
while (q--)
{
int op = read(), u = read(), v, x, p, q;
switch (op)
{
case 1:
rt = u;
break;
case 2:
v = read(), x = read();
u = getlca(u, v, rt);
if (u == rt)
{
update(1, 1, n, x);
}
else if (lca(u, rt) == u)
{
v = getfa(rt, dep[rt] - dep[u] - 1);
update(1, 1, n, x);
update_subtree(v, -x); //将v的子树减掉
}
else
{
update_subtree(u, x);
}
break;
case 3:
if (u == rt)
{
write(query(1, 1, n));
}
else if (lca(rt, u) == u)
{
v = getfa(rt, dep[rt] - dep[u] - 1);
write(query(1, 1, n) - query_subtree(v));
}
else
{
write(query_subtree(u));
}
putchar('\n');
break;
}
}
return 0;
}

