【题解】Luogu-P5303 [GXOI/GZOI2019]逼死强迫症
Preface
矩阵题的登峰造极之作。
Description
有 \(T\) 组数据。
对于每组数据,给定正整数 \(N\),请求出用 \((N-1)\) 个 \(2\times 1\) 的方格和 \(2\) 个 \(1\times 1\) 的方格铺满 \(2\times N\) 的大方格的方案数,其中 \(2\) 个 \(1\times 1\) 的方格不能有相邻的边。
- 答案对 \(10^9+7\) 取模。
- 对于 \(100\%\) 的数据,\(N\le 2\times 10^9,T\le 500\)。
Solution
前置芝士:
- 一定的小奥基础
- 矩阵快速幂
第一部分:何为所求
这两个 \(1\times 1\) 一定能框出一个 \(2\times m\) 的长方形,其中因为不能相邻,所以 \(m\ge 3\)。
考虑这 \(2\) 个 \(1\times 1\) 的摆放位置:同行或异行。
举个例子:
当 \(m\) 为偶数时:
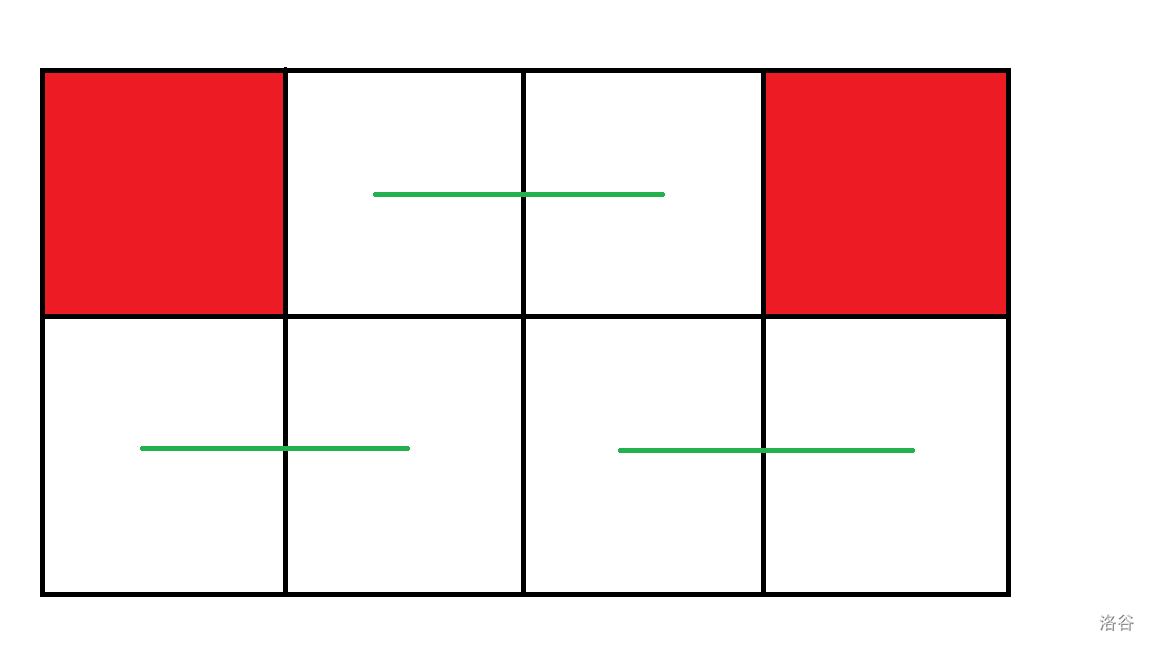
同行是可以的,而且这个长方形内只有 \(1\) 种方法。
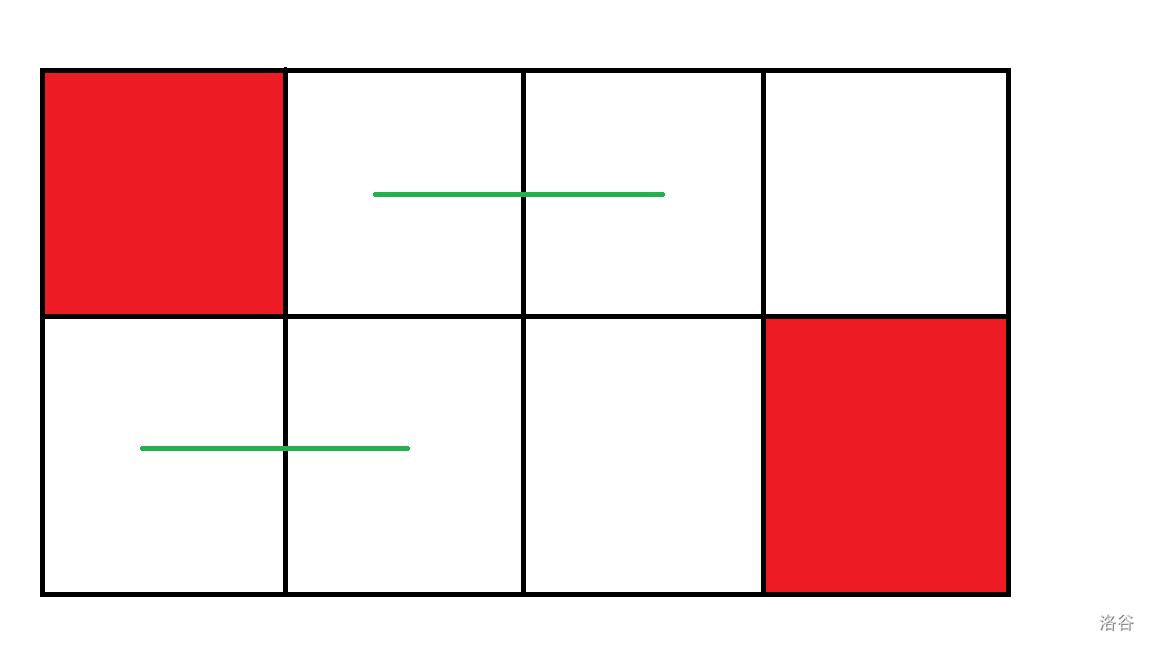
异行是不行的。
当 \(m\) 为奇数时:
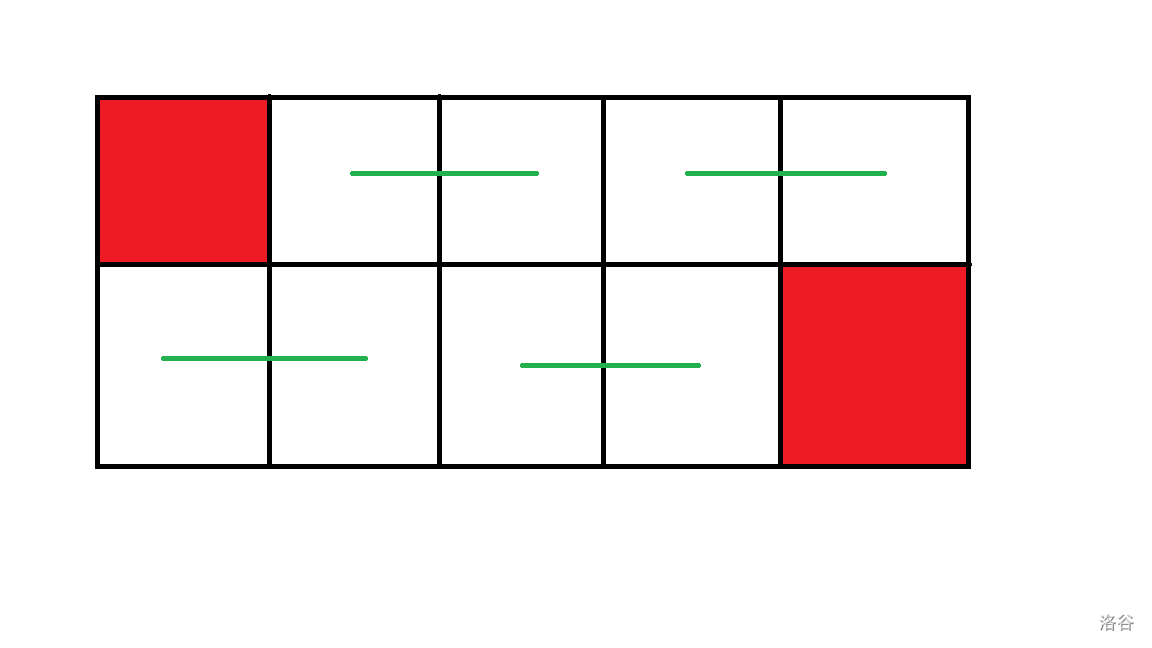
异行是可以的,而且这个长方形内只有 \(1\) 种方法。
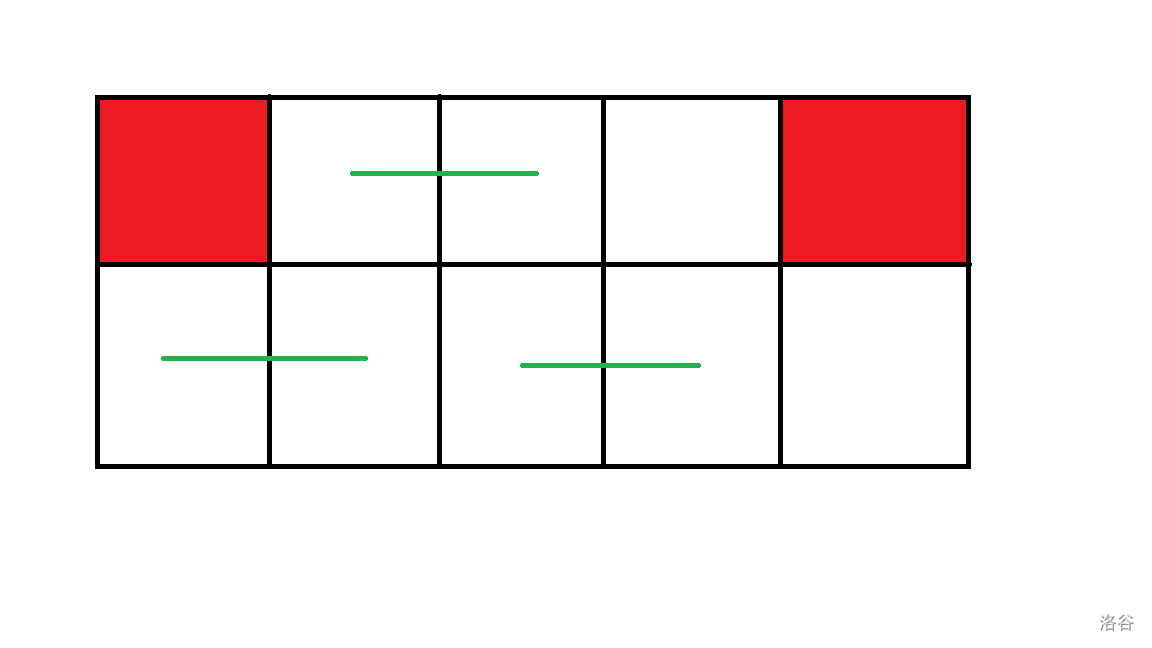
同行是不行的。
综上可以发现无论 \(m\) 的奇偶性,框出的 \(2\times m\) 有且仅有一种方法。
是吗?
因为 \(2\) 个小正方形的位置可以上下调换,所以这两种都需要乘 \(2\)。
再考虑全部:
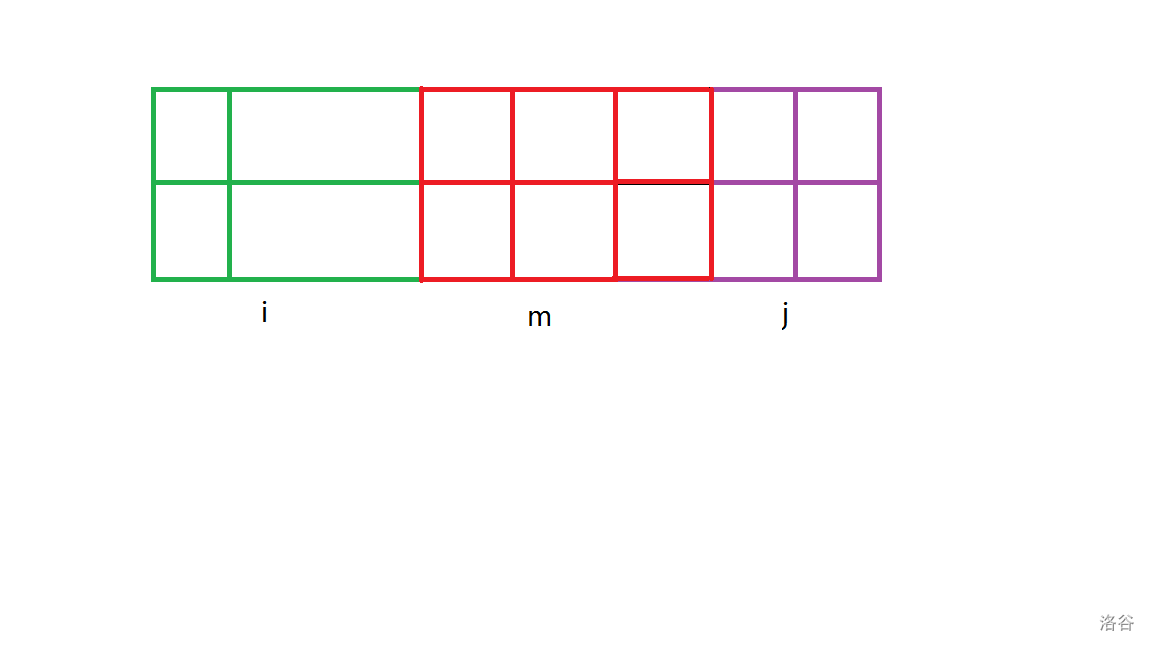
左右两边都是形如 \(2\times k\) 的长方形,根据小学奥数可知用 \(k\) 个 \(2\times 1\) 的覆盖 \(2\times k(k\in\mathbf{N})\) 的有 \(F_k\) 种(其中 \(\{F_k\}\) 为斐波那契数列,下标从 \(0\) 开始)。
确定了两边的 \(i,j\),中间的 \(m\) 就自动确定了。
中间是 \(2\) 个 \(1\times 1\) 的框出的长方形,有 \(2\) 种方法,又 \(m\ge 3\),所以
二、推式子
根据斐波那契数列的前缀和 \(\sum\limits_{i=0}^n F_i=F_{n+2}-1\),有
令 \(S_n=\sum\limits_{i=0}^n F_n\cdot F_{n-i}\),则
现在的问题就是如何求出 \(S_n\)。
可以用矩阵快速幂解决:
那么矩阵就是
初始值为
\(ans=2(1+S_{n-1}-2F_{n-1}-F_{n-2})\),所以求 \(S_{n-1}\) 乘 \((n-2)\) 次转移矩阵即可。
时间复杂度为 \(O(T\cdot 64\log n)\)。
Code
//18 = 9 + 9 = 18.
#include <iostream>
#include <cstdio>
#include <cstring>
#define Debug(x) cout << #x << "=" << x << endl
#define int long long
using namespace std;
struct matrix
{
int a[5][5];
matrix()
{
memset(a, 0, sizeof(a));
}
void build()
{
for (int i = 1; i <= 4; i++)
{
a[i][i] = 1;
}
}
};
const int MOD = 1e9 + 7;
matrix operator *(matrix x, matrix y)
{
matrix res;
for (int k = 1; k <= 4; k++)
{
for (int i = 1; i <= 4; i++)
{
if (!x.a[i][k])
{
continue;
}
for (int j = 1; j <= 4; j++)
{
res.a[i][j] = (res.a[i][j] + x.a[i][k] * y.a[k][j] % MOD) % MOD;
}
}
}
return res;
}
matrix qpow(matrix a, int b)
{
matrix base = a, ans;
ans.build();
while (b)
{
if (b & 1)
{
ans = ans * base;
}
base = base * base;
b >>= 1;
}
return ans;
}
signed main()
{
int t;
scanf("%lld", &t);
matrix base;
base.a[1][1] = base.a[1][2] = base.a[1][3] = base.a[1][4] = base.a[2][1] = base.a[3][3] = base.a[3][4] = base.a[4][3] = 1; //转移矩阵
matrix fst;
fst.a[1][1] = 2, fst.a[2][1] = fst.a[3][1] = fst.a[4][1] = 1; //初始矩阵
while (t--)
{
int n;
scanf("%lld", &n);
if (n == 1)
{
puts("0");
continue;
}
matrix res = qpow(base, n - 2) * fst;
int S = res.a[1][1], F1 = res.a[3][1], F2 = res.a[4][1]; //S : S_{n-1}, F1 : F_{n-1}, F2 : F_{n-2}
printf("%lld\n", (((1 + S - (F1 << 1) - F2) << 1) % MOD + MOD) % MOD);
}
return 0;
}
Reference
- [1] Great_Influence:题解 P5303 【[GXOI/GZOI2019]逼死强迫症】
- [2] StudyingFather:[洛谷 5303,loj 3086][GXOI/GZOI2019]逼死强迫症

