经典卷积神经网络 - LeNet

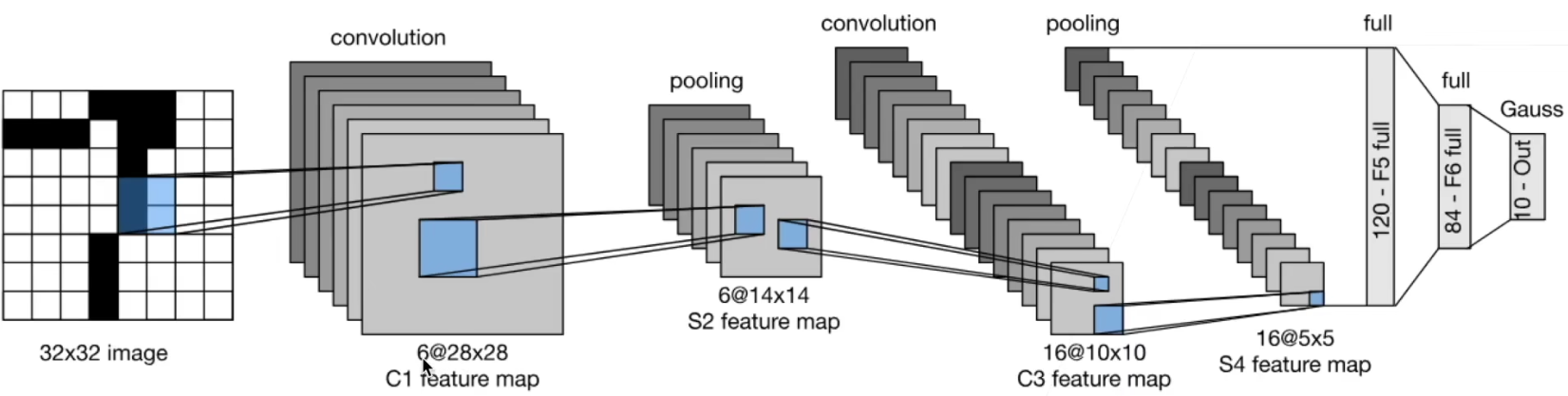
该模型用于手写的数字识别。
LeNet模型包含了多个卷积层和池化层，以及最后的全连接层用于分类。其中，每个卷积层都包含了一个卷积操作和一个非线性激活函数，用于提取输入图像的特征。池化层则用于缩小特征图的尺寸，减少模型参数和计算量。全连接层则将特征向量映射到类别概率上。

MNISt数据集

50000个训练数据，10000个测试数据。图像大小为28x28，共10类（0～9）。

• LeNet是早期成功的神经网络
• 先使用卷积层来学习图片空间信息
• 然后使用全连接层来转换到类别空间

对于padding

通用的卷积时padding 的选择

如卷积核宽高为3时 padding 选择1

如卷积核宽高为5时 padding 选择2

如卷积核宽高为7时padding选择3

至于选择填充多少像素，通常有两个选择，分别叫做Valid卷积和Same卷积。

Valid卷积意味着不填充，这样的话，如果你有一个$n\times n$的图像，用一个$f\times f$的过滤器卷积，它将会给你一个$(n-f+1)\times (n-f+1)$维的输出。例如，有一个6×6的图像，通过一个3×3的过滤器，得到一个4×4的输出。

Same卷积意味你填充后，你的输出大小和输入大小是一样的。根据这个公式$n-f+1$，当你填充$p$个像素点，n就变成了$n+2p$，最后公式变为$n+2p-f+1$。因此如果你有一个$n\times n$的图像，用$p$个像素填充边缘，输出的大小就是这样的$(n+2p-f+1)\times (n+2p-f+1)$。如果你想让$(n+2p-f+1)=n$的话，使得输出和输入大小相等，如果你用这个等式求解$p$，那么$p=(f-1)/2$。所以当$f$是一个奇数的时候，只要选择相应的填充尺寸，你就能确保得到和输入相同尺寸的输出。

代码实现

LeNet（LeNet-5）由两个部分组成：卷积编码器和全连接层密集块。

model.py

from torch import nn

class Reshape(nn.Module):
    def forward(self,x):
        return x.reshape((-1,1,28,28))

class MyLeNet(nn.Module):
    def __init__(self, *args, **kwargs) -> None:
        super().__init__(*args, **kwargs)
        # 假如sigmoid激活函数后 损失不下降
        self.model = nn.Sequential(
            Reshape(),
            nn.Conv2d(1,6,kernel_size=5,padding=2),
            nn.Sigmoid(),
            nn.AvgPool2d(2,stride=2),
            nn.Conv2d(6,16,kernel_size=5),
            nn.Sigmoid(),
            nn.AvgPool2d(2,stride=2),
            nn.Flatten(),
            nn.Linear(16*5*5,120),
            nn.Linear(120,84),
            nn.Linear(84,10)
        )

    def forward(self,x):
        return self.model(x)

train.py

# 扫描数据次数
epochs = 20
# 分组大小
batch = 64
# 学习率
learning_rate = 0.05
# 训练次数
train_step = 0
# 测试次数
test_step = 0


# 定义图像转换
transform = transforms.Compose([
    transforms.ToTensor()
])
# 读取数据
train_dataset = datasets.MNIST(root="./dataset",train=True,transform=transform,download=True)
test_dataset = datasets.MNIST(root="./dataset",train=False,transform=transform,download=True)
# 加载数据
train_dataloader = DataLoader(train_dataset,batch_size=batch,shuffle=True,num_workers=0)
test_dataloader = DataLoader(test_dataset,batch_size=batch,shuffle=True,num_workers=0)
# 数据大小
train_size = len(train_dataset)
test_size = len(test_dataset)
print("训练集大小：{}".format(train_size))
print("验证集大小：{}".format(test_size))

# GPU
device = torch.device("mps" if torch.backends.mps.is_available() else "cpu")

# 创建网络
net = MyLeNet()
net = net.to(device)
# 定义损失函数
loss = nn.CrossEntropyLoss()
loss = loss.to(device)
# 定义优化器
optimizer = torch.optim.SGD(net.parameters(),lr=learning_rate)

writer = SummaryWriter("logs")
# 训练
for epoch in range(epochs):
    print("-------------------第 {} 轮训练开始-------------------".format(epoch))
    net.train()
    for data in train_dataloader:
        train_step = train_step + 1
        images,targets = data
        images = images.to(device)
        targets = targets.to(device)
        outputs = net(images)
        loss_out = loss(outputs,targets)
        optimizer.zero_grad()
        loss_out.backward()
        optimizer.step()

        if train_step%100==0:
            writer.add_scalar("Train Loss",scalar_value=loss_out.item(),global_step=train_step)
            print("训练次数：{}，Loss：{}".format(train_step,loss_out.item()))

    # 测试
    net.eval()
    total_loss = 0
    total_accuracy = 0
    with torch.no_grad():
        for data in test_dataloader:
            test_step = test_step + 1
            images, targets = data
            images = images.to(device)
            targets = targets.to(device)
            outputs = net(images)
            loss_out = loss(outputs, targets)
            total_loss = total_loss + loss_out
            accuracy = (targets == torch.argmax(outputs,dim=1)).sum()
            total_accuracy = total_accuracy + accuracy
        # 计算精确率
        print(total_accuracy)
        accuracy_rate = total_accuracy / test_size

        print("第 {} 轮，验证集总损失为：{}".format(epoch+1,total_loss))
        print("第 {} 轮，精确率为：{}".format(epoch+1,accuracy_rate))
        writer.add_scalar("Test Total Loss",scalar_value=total_loss,global_step=epoch+1)
        writer.add_scalar("Accuracy Rate",scalar_value=accuracy_rate,global_step=epoch+1)
    torch.save(net,"./model/net_{}.pth".format(epoch+1))
    print("模型net_{}.pth已保存".format(epoch+1))