时间序列模型
自然语言处理的输入输出基本上都是序列,序列问题是自然语言处理最本质的问题。
序列模型:就是输入输出均为序列数据的模型,序列模型将输入序列数据转换为目标序列数据。
序列数据
-
实际上很多数据是有时序结构的
-
电影的评价随时间变化而变化
- 拿奖后评分上升,直到奖项被忘记
- 看了很多好电影后,人们的期望变高
- 季节性:贺岁片、暑期档
- 导演、演员的负面报道导致评分变低
-
音乐、语言、文本和视频都是连续的
-
大地震发生后,很可能会有几次较小的余震
-
人的互动是连续的
-
预测明天的股价要比填补昨天遗失的股价更困难
统计工具
-
在时间 t t t观察到 x t x_t xt,那么得到 T T T个不独立的随机变量 ( x 1 , . . . , x t ) (x_1,...,x_t) (x1,...,xt)~ p ( X ) p(X) p(X)
-
使用条件概率展开
p ( a , b ) = p ( a ) p ( b ∣ a ) = p ( b ) p ( a ∣ b ) p(a,b) = p(a)p(b|a) = p(b)p(a|b) p(a,b)=p(a)p(b∣a)=p(b)p(a∣b)
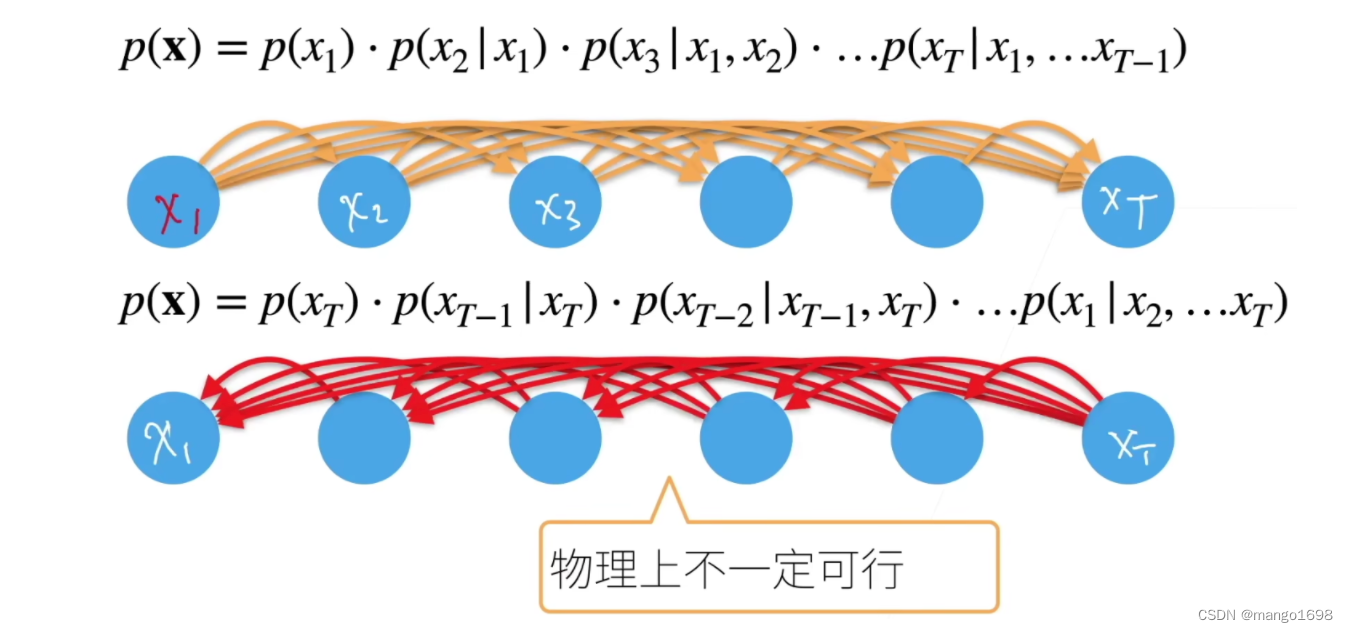
对条件概率建模:
p ( x t ∣ x 1 , . . . , x t − 1 ) = p ( x t ∣ f ( x 1 , . . . , x t − 1 ) ) p(x_t|x_1,...,x_{t-1}) = p(x_t|f(x_1,...,x_{t-1})) p(xt∣x1,...,xt−1)=p(xt∣f(x1,...,xt−1))
对见过的数据建模,也成自回归模型。
核心事情:怎么算 f ( x 1 , . . . , x t − 1 ) f(x_1,...,x_{t-1}) f(x1,...,xt−1)
方案A - 马尔科夫假设
p ( X ) = p ( x 1 ) ⋅ p ( x 2 ∣ x 1 ) ⋅ p ( x 3 ∣ x 1 , x 2 ) ⋅ . . . ⋅ p ( x T ∣ x 1 , . . . , x T − 1 ) p(X) = p(x_1)·p(x_2|x_1)·p(x_3|x_1,x_2)·...·p(x_T|x_1,...,x_{T-1}) p(X)=p(x1)⋅p(x2∣x1)⋅p(x3∣x1,x2)⋅...⋅p(xT∣x1,...,xT−1)
假设当前数据只跟 τ \tau τ个过去数据点相关

p
(
x
t
∣
x
1
,
.
.
.
,
x
t
−
1
)
=
p
(
x
t
∣
f
(
x
t
−
τ
,
.
.
.
,
x
t
−
1
)
)
=
p
(
x
t
∣
f
(
x
t
−
τ
,
.
.
.
,
x
t
−
1
)
)
p(x_t|x_1,...,x_{t-1}) = p(x_t|f(x_{t-\tau},...,x_{t-1}))=p(x_t|f(x_{t-\tau},...,x_{t-1}))
p(xt∣x1,...,xt−1)=p(xt∣f(xt−τ,...,xt−1))=p(xt∣f(xt−τ,...,xt−1))
方案B - 潜变量模型
p
(
X
)
=
p
(
x
1
)
⋅
p
(
x
2
∣
x
1
)
⋅
p
(
x
3
∣
x
1
x
2
)
⋅
.
.
.
⋅
p
(
x
T
∣
x
1
,
.
.
.
,
x
T
−
1
)
p(X) = p(x_1)·p(x_2|x_1)·p(x_3|x_1x_2)·...·p(x_T|x_1,...,x_{T-1})
p(X)=p(x1)⋅p(x2∣x1)⋅p(x3∣x1x2)⋅...⋅p(xT∣x1,...,xT−1)
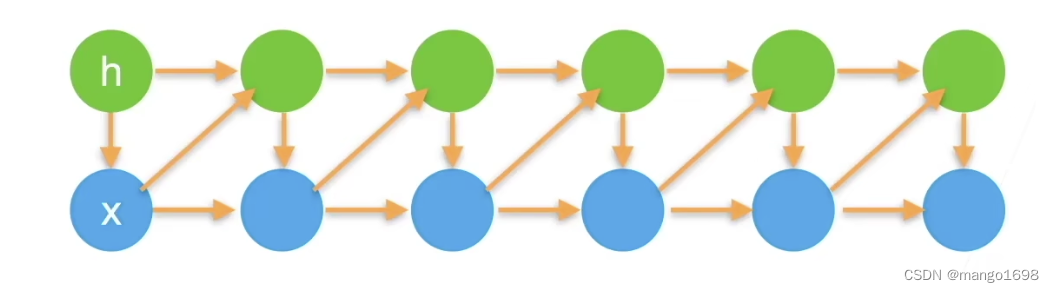
引入潜变量
h
t
h_t
ht来表示过去信息
h
t
=
f
(
x
1
,
.
.
.
,
x
t
−
1
)
h_t=f(x_1,...,x_{t-1})
ht=f(x1,...,xt−1)
这样 x t = p ( x t ∣ h t ) x_t=p(x_t|h_t) xt=p(xt∣ht)
总结:
- 时序模型中,当前数据跟之前观察到的数据相关
- 自回归模型使用自身过去数据来预测未来
- 马尔科夫模型假设当前只跟最近少数数据相关,从而简化模型
- 潜变量模型使用潜变量来概括历史信息



