深度学习笔记 - 刘二大人
1. 梯度下降与反向传播
梯度下降、随机梯度下降、批量随机梯度下降
- 梯度下降:所有数据一起求损失、求平均,进行梯度下降,可并行,但是效果不好
- 随机梯度下降:每一个样本数据单独进行梯度下降,不可并行,效果好,但是费时间
- 批量随机梯度下降:将数据进行分组(batch),对上述两组方法进行中和。batch,原来是指全部数据,所以更正式的是称为mini-batch。
矩阵求导书籍:Matrix cookbook
线性变换,无论使用多少层,最终都可以化简为一层。
为了解决这个问题,对每一层最终输出加一个非线形变换函数,即激活函数,如sigmoid、softmax,ReLU等。
Tensor包含data: w w w,和grad: ∂ l o s s ∂ w \frac{\partial{loss}}{\partial{w}} ∂w∂loss
torch.tensor([0,1])
w.requires_grad = True # 计算梯度,默认为False
l = loss(x,y)
l.backward() # 反向传播,将链路上需要梯度的,计算出来,梯度存到变量(Tensor)w的grad中,然后计算图会被释放掉
w.data = w.data - 0.01*w.grad.detach # 之前使用.data,现在.data被弃用,如果直接使用w.grad,则会建立计算图
在求损失总和时,因为l=loss(x,y)求出的l是一个Tensor,直接相加,会建立计算图,占用内存,正确的是提取l.item(),如
total_loss += l.item() # .item:把tensor转为python的float类型
Tensor类型书籍参与运算时会建立计算图
w.grad.data.zero_() # 将权重变量中梯度的数据清零,如果不清零,梯度会累加
w.grad.item():用于获取标量张量中的数值,适用于有一个元素的张量w.grad.data:已弃用,用于获取梯度张量的数据部分,这是一个包含梯度值的张量w.grad.detach():用于将梯度张量从计算图中分离出来,这样不会再建立计算图
构建神经网络步骤:
- 准备数据
- 设计模型
- 构造损失函数和优化器
- 训练(前馈、反馈、更新)
optimizer.zero_grad()虽然当前计算图中的梯度被清零,但是在优化器步骤中使用的梯度信息仍然存在于参数的.grad属性中。
在Pytorch中,有两个空间存储了梯度信息:
- 计算图中的梯度
- 模型参数的
.grad属性
2. Logistic回归
Sigmoid函数包含:
-
σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1+e^{-x}} σ(x)=1+e−x1
-
e r f ( π 2 x ) erf(\frac{\sqrt\pi}{2}x) erf(2πx)
-
x 1 + x 2 \frac{x}{\sqrt{1+x^2}} 1+x2x
-
t a n h ( x ) tanh(x) tanh(x)
-
2 π a r c t a n ( π 2 x ) \frac{2}{\pi}arctan(\frac{\pi}{2}x) π2arctan(2πx)
-
2 π g d ( π 2 x ) \frac{2}{\pi}gd(\frac{\pi}{2}x) π2gd(2πx)
-
x 1 + ∣ x ∣ \frac{x}{1+|x|} 1+∣x∣x
tanh(x)为双曲正切函数,在循环神经网络中经常使用。

这些函数都被称为sigmoid函数,但是 1 1 + e − x \frac{1}{1+e^{-x}} 1+e−x1函数(Logistic函数)最出名,所以人们习惯将其直接称为sigmoid函数。

模型更改后,损失函数也要变化,之前我们使用的MSE,即
l
o
s
s
=
(
y
^
−
y
)
2
=
(
x
⋅
w
−
y
)
2
loss=(\hat y - y)^2=(x·w-y)^2
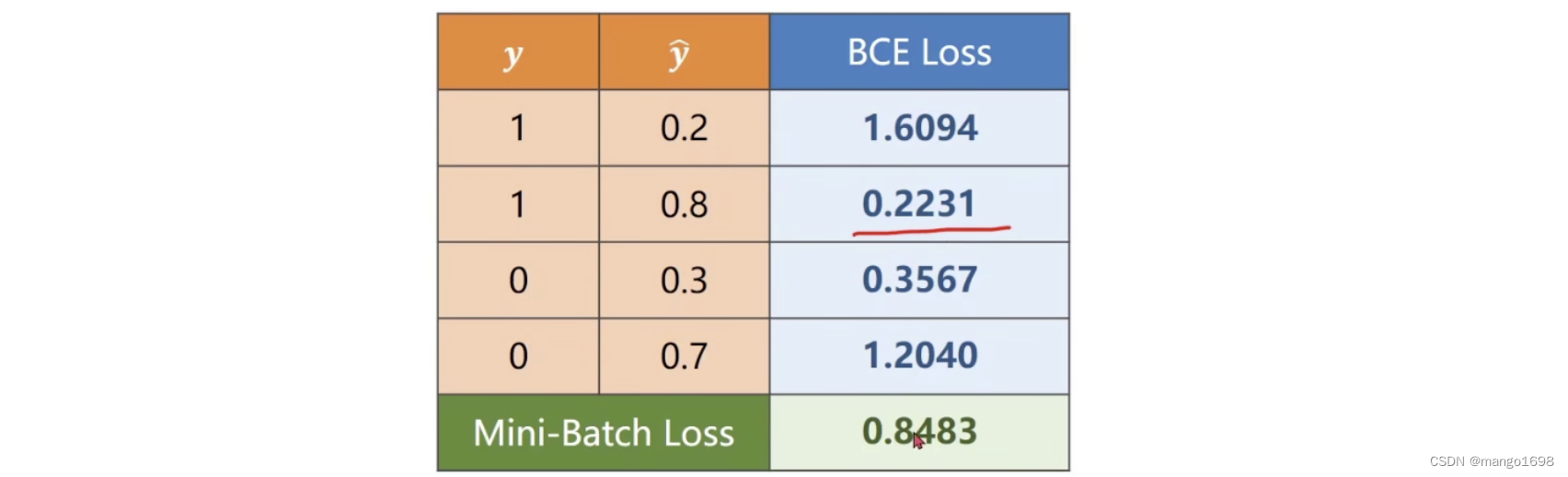
loss=(y^−y)2=(x⋅w−y)2要更改为BCE损失,即二元交叉熵损失函数。交叉熵损失函数为CE Loss(Cross-Entropy Loss)。
l
o
s
s
=
−
(
y
l
o
g
y
^
+
(
1
−
y
)
l
o
g
(
1
−
y
^
)
)
loss = -(ylog\hat y+(1-y)log(1-\hat y))
loss=−(ylogy^+(1−y)log(1−y^))
实际上是求两个分布的差异的大小。
loss_func = torch.nn.BCELoss(size_average=False) # size_average:是否给每一个批量求均值,影响如何选择学习率
# size_average被弃用,使用reduction属性进行替代
# size_average=True -> reduction='mean'
# size_average=False -> reduction='sum'
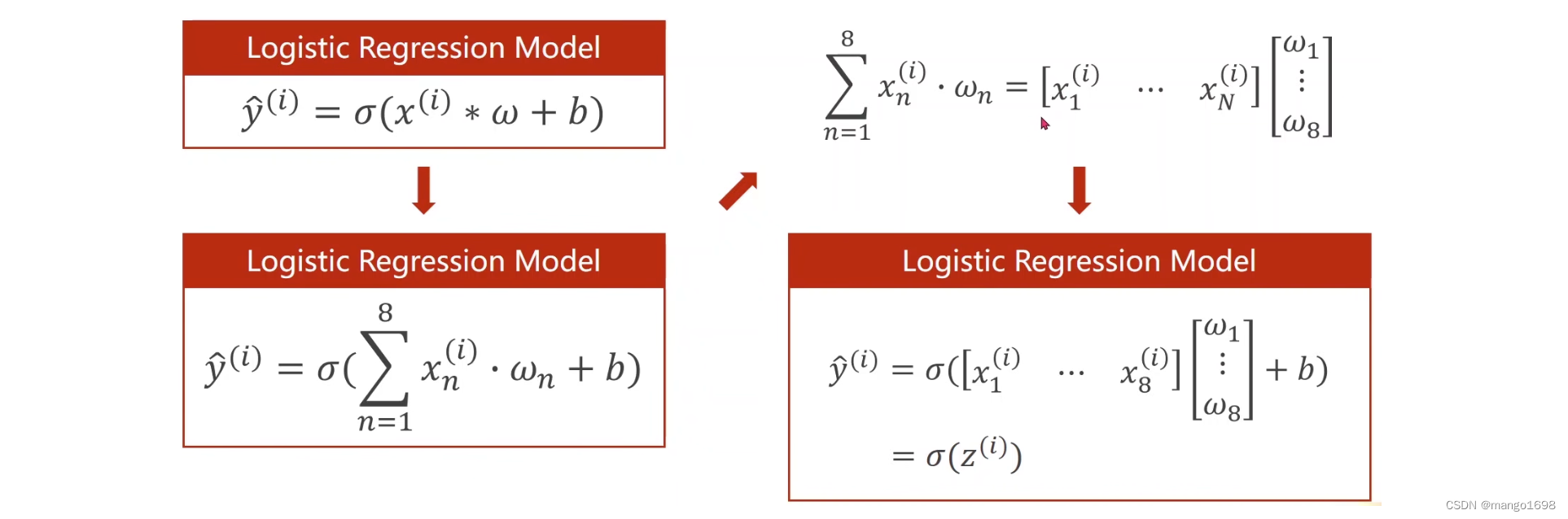
3. 处理多维特征的输入

4. 加载数据集
实现Dataset
注意:Dataset是一个抽象类
我们定义自己的数据集,就要继承Dataset这个抽象类
import torch
from torch.utils.data import DataLoader,Dataset
class DiabetesDataset(Dataset):
def __init__(self):
pass
# 允许对象进行下标操作
def __getitem__(self, item):
pass
# 允许通过len(对象)来获取数据集的大小
def __len__(self):
pass
__getitem__:允许对象通过下标进行操作
__len__:允许通过len(对象),来获取数据集的大小
在__init__中我们有两种选择:
- 把所有的数据都读到内存里面,适用于小数据集
- 初始化存储数据的文件名/文件地址,通过
__getitem__读取数据的时候再将数据加载进内存

代码实现:
import torch
from torch.utils.data import DataLoader,Dataset
import numpy as np
class DiabetesDataset(Dataset):
def __init__(self,filepath):
xy = np.loadtxt(filepath,delimiter=',',dtype=np.float32)
self.len = xy.shape[0]
self.x_data = torch.from_numpy(xy[:,:-1])
self.y_data = torch.from_numpy(xy[:,[-1]])
# 允许对象进行下标操作
def __getitem__(self, index):
return self.x_data[index],self.y_data[index]
# 允许通过len(对象)来获取数据集的大小
def __len__(self):
return self.len
data = DiabetesDataset('./data/diabetes.csv')
train_data = DataLoader(data,batch_size=64,shuffle=True,num_workers=0)
5. 多分类问题

Softmax激活函数:
P
(
y
=
i
)
=
e
Z
i
∑
j
=
0
K
−
1
e
Z
j
i
∈
{
0
,
.
.
.
,
K
−
1
}
P(y=i)=\frac{e^{Z_i}}{\sum_{j=0}^{K-1}e^{Z_j}}\ \ \ i\in\{0,...,K-1\}
P(y=i)=∑j=0K−1eZjeZi i∈{0,...,K−1}

在pytorch中,交叉熵损失包含了softmax,所以神经网络的最后一层不再需要我们家softmax激活函数。
注:CrossEntorpyLoss <==> LogSoftmax + NLLLoss
6. 卷积神经网络
下采样:通道数不变,特征图大小改变

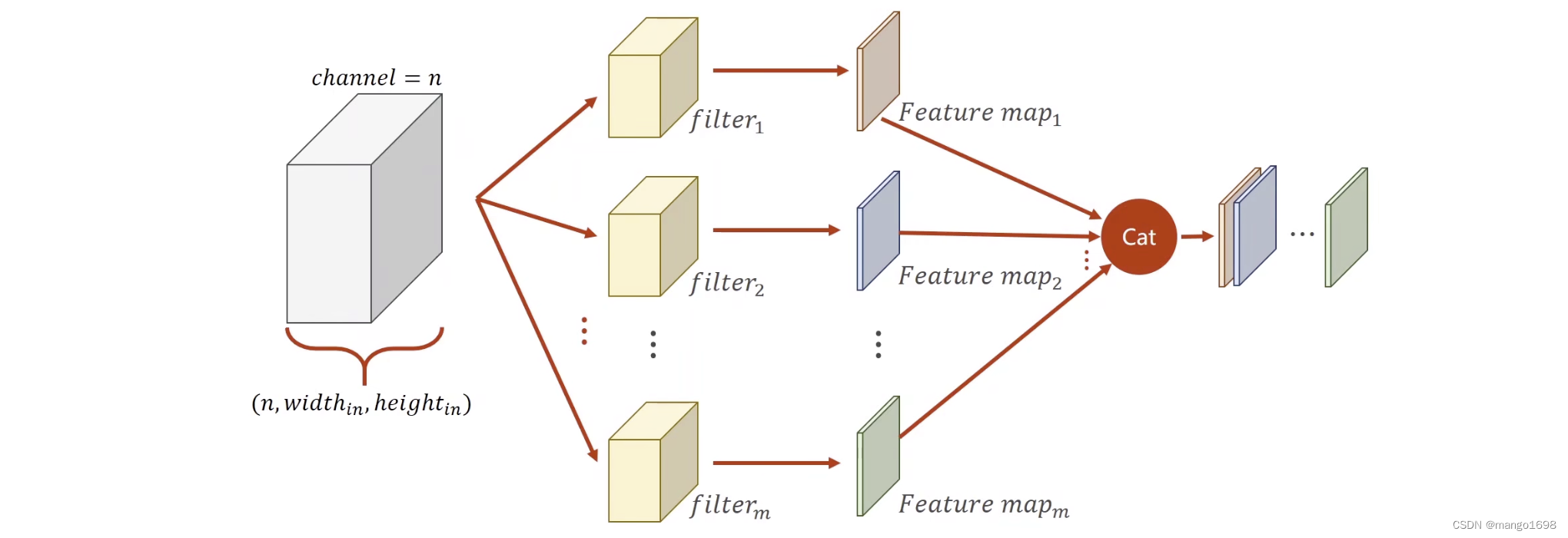
对于复杂的网络,在定义网络时,
- 要减少代码的冗余:
- 使用函数
- 使用类

如GoogLeNet,我们将如图中红圈画出来的框,称为Inception。
Inception块
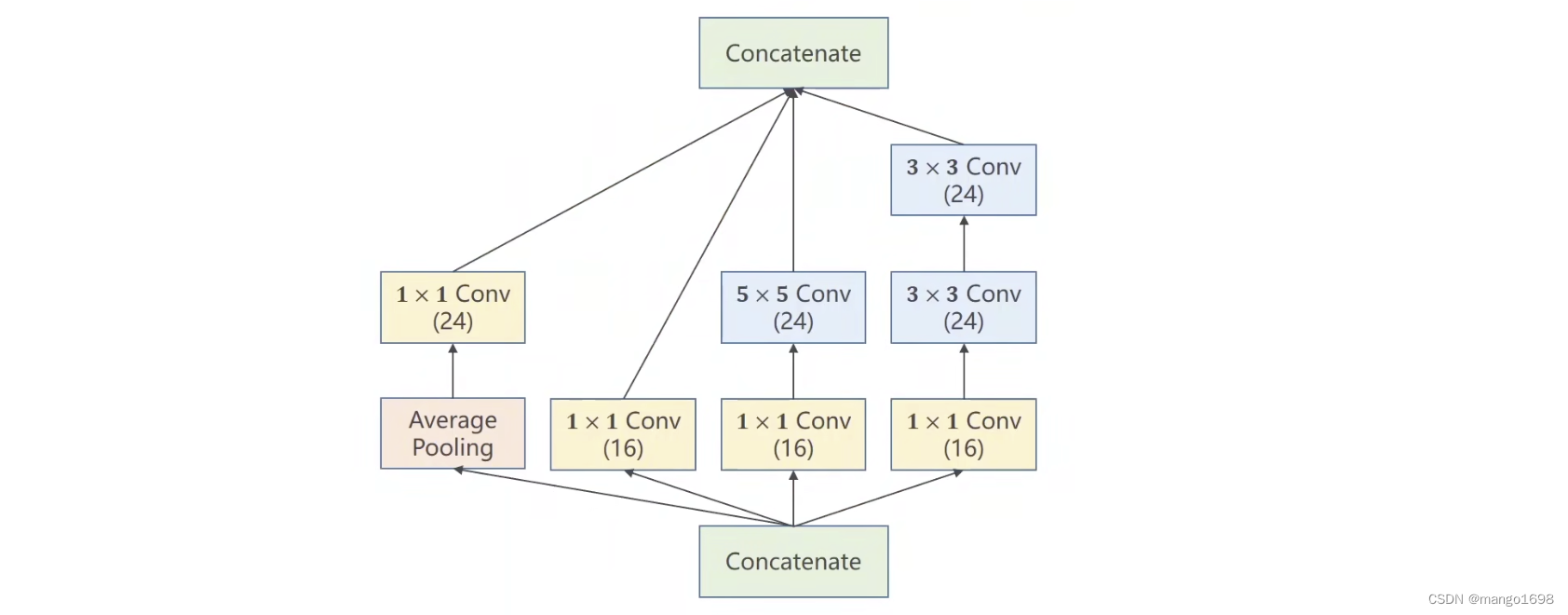
我们在构造神经网络时,有些超参数是比较难选的,如卷积核的大小Kernel,所以GoogLeNet就在一个Inception块使用多个卷积,然后将结果摞在一起,比如如果3x3的卷积好用,那么3x3的权重就会变的比较大,其他路线上的权重就会变小。一句话说,就是提供了几种候选的配置,然后通过训练,在候选配置中找到最优的卷积组合。
Concatenate:将张量拼接到一起,沿着通道进行拼接。 但是,注意,对于这些候选的路径,最后拼接之前要保证特征图的宽度和高度一致。
**1x1卷积:**改变通道数量。
FLOPS(S大写):指每秒浮点运算次数。用来衡量硬件的性能。
FLOPs(S小写):浮点运算次数,可以用来衡量算法/模型复杂度。
FLOPs运算量计算方法:

输入通道大小192,图像大小28x28,卷积核大小:5x5,输出通道为32。
F
L
O
P
s
=
w
×
h
×
k
2
×
c
×
c
′
F
L
O
P
s
=
28
×
28
×
5
2
×
192
×
32
FLOPs = w\times h \times k^2 \times c \times c' \\ FLOPs = 28 \times 28 \times 5^2\times 192 \times 32
FLOPs=w×h×k2×c×c′FLOPs=28×28×52×192×32
在神经网络中,我们最大的问题是运算量太大,所以我们要想办法来降低运算量。所以就提出用1x1的卷积来改变通道数量,以降低通道数量来减少运算量。
代码实现Inception:
import torch
from torch import nn
class Inception(nn.Module):
def __init__(self,in_channel, *args, **kwargs) -> None:
super().__init__(*args, **kwargs)
self.branch_pool_1 = nn.AvgPool2d(3,1,1)
self.branch_pool_2 = nn.Conv2d(in_channel,24,1)
self.branch1x1 = nn.Conv2d(in_channel,out_channels=16,kernel_size=1,stride=1)
self.branch5x5_1 = nn.Conv2d(in_channel,out_channels=16,kernel_size=1)
self.branch5x5_2 = nn.Conv2d(16,out_channels=24,kernel_size=5,padding=2)
self.branch3x3_1 = nn.Conv2d(in_channel,out_channels=16,kernel_size=1,stride=1)
self.branch3x3_2 = nn.Conv2d(16,out_channels=24,kernel_size=3,padding=1)
self.branch3x3_3 = nn.Conv2d(24,out_channels=24,kernel_size=3,padding=1)
def forward(self,x):
branch_pool = self.branch_pool_1(x)
branch_pool = self.branch_pool_2(branch_pool)
branch1x1 = self.branch1x1(x)
branch5x5 = self.branch5x5_1(x)
branch5x5 = self.branch5x5_2(branch5x5)
branch3x3 = self.branch3x3_1(x)
branch3x3 = self.branch3x3_2(branch3x3)
branch3x3 = self.branch3x3_3(branch3x3)
# 拼接
outputs = [branch_pool,branch1x1,branch5x5,branch3x3]
# dim = 1 是因为 张量的维度为(b,c,w,h) 1:c 1为通道
return torch.cat(outputs,dim=1)
定义完整的网络
import torch
from torch import nn
from torch.nn import functional as F
class Net(nn.Module):
def __init__(self, *args, **kwargs) -> None:
super().__init__(*args, **kwargs)
self.conv1 = nn.Conv2d(1,10,kernel_size=5)
self.conv2 = nn.Conv2d(88,20,kernel_size=5)
self.incep1 = Inception(in_channel=10)
self.incep2 = Inception(in_channel=20)
self.mp = nn.MaxPool2d(2)
self.fc = nn.Linear(1408,10)
def forward(self,x):
in_size = x.size(0)
x = F.relu(self.mp(self.conv1(x)))
x = self.incep1(x)
x = F.relu(self.mp(self.conv2(x)))
x = self.incep2(x)
x = x.view(in_size,-1)
x = self.fc(x)
return x
梯度消失:
根据链式法则:是很多像的导数连乘,若倒数都是<1的,那么连乘项很多,值就会取向余0,则会出现梯度消失。
为了应对梯度消失问题,提出过一些训练方法:对网络进行逐层的训练。如下图,将第一个隐藏层锁住,不进行参数更更新,只对第二个隐藏层进行训练,训练完成后,再将第一、第二隐藏层都锁住,再加上第三个隐藏层,对第三个隐藏层进行训练,重复此过程。

Residual net(ResNet):
残差网络。

ResNet可以解决梯度消失问题,因为 ∂ Z ∂ x = ∂ F ∂ x + 1 \frac{\partial Z}{\partial x} = \frac{\partial F}{\partial x} + 1 ∂x∂Z=∂x∂F+1,当第一项趋向于0的时候,整体的值也会趋向于1。
残差块代码实现:
from torch.nn import functional as F
from torch import nn
class ShortCut(nn.Module):
def __init__(self,in_channel,out_channel,kernel_size=3,padding=1,stride=1, *args, **kwargs) -> None:
super().__init__(*args, **kwargs)
self.conv1 = nn.Conv2d(in_channel,out_channel,kernel_size=kernel_size,padding=padding,stride=stride)
self.conv2 = nn.Conv2d(out_channel,out_channel,kernel_size=kernel_size,padding=padding,stride=stride)
if in_channel!=out_channel:
self.conv1x1 = nn.Conv2d(in_channel,out_channel,kernel_size=1,padding=0)
else:
self.conv1x1 = nn.Identity()
self.bn1 = nn.BatchNorm2d(out_channel)
self.bn2 = nn.BatchNorm2d(out_channel)
def forward(self,x):
p1 = F.relu(self.bn1(self.conv1(x)))
p1 = self.bn2(self.conv2(p1))
p2 = self.conv1x1(x)
output = p1 + p2
output = F.relu(output)
return output
if __name__ == '__main__':
net = ShortCut(3,10)
x = torch.ones((64,3,447,447))
out = net(x)
print(out.shape)
nn.Identity()是 PyTorch 中的一个特殊模块,它代表恒等映射(identity mapping)。在残差块中,为了确保残差块的输入和输出维度相匹配,可能需要对输入进行一些变换。如果输入和输出的通道数相同,就不需要进行变换,此时可以使用
nn.Identity(),它不进行任何操作,直接返回输入。
7. 循环神经网络
用来处理带有序列模式的数据。使用权重共享,来减少需要训练的权重的数量。

x t x_t xt:序列当中时刻t的数据。
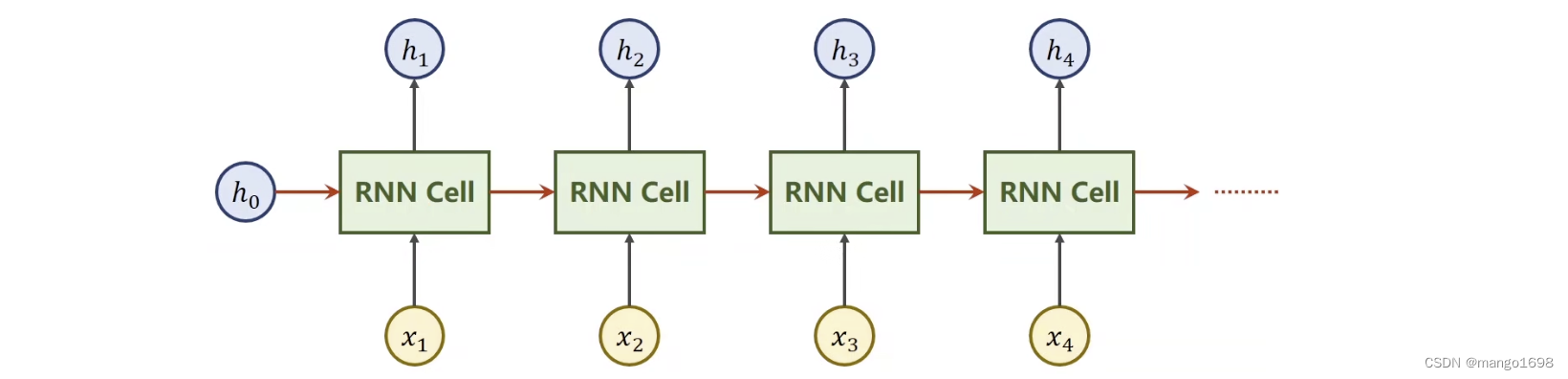
RNN Cell:本质是一个线性层,线性层可以把某一个维度映射到另外一个维度空间里面。与我们平常使用的线性层不同,这个线性层是共享的。

h 0 h_0 h0是先验知识,传入到RNN Cell,如果没有鲜艳,那就将 h 0 h_0 h0设置为与 h 1 , h 2 . . h_1,h_2.. h1,h2..维度相同的全零。
RNN整体过程,
h
0
,
x
1
h_0,x_1
h0,x1经过某种运算,生成
h
1
h_1
h1,将
h
1
h_1
h1作为输出送到下一个RNN Cell中,同时将
h
1
h_1
h1作为一个输出,然后在下一个RNN Cell中,将
h
1
,
x
2
h_1,x_2
h1,x2作为输入进行运算,输入
h
2
h_2
h2。
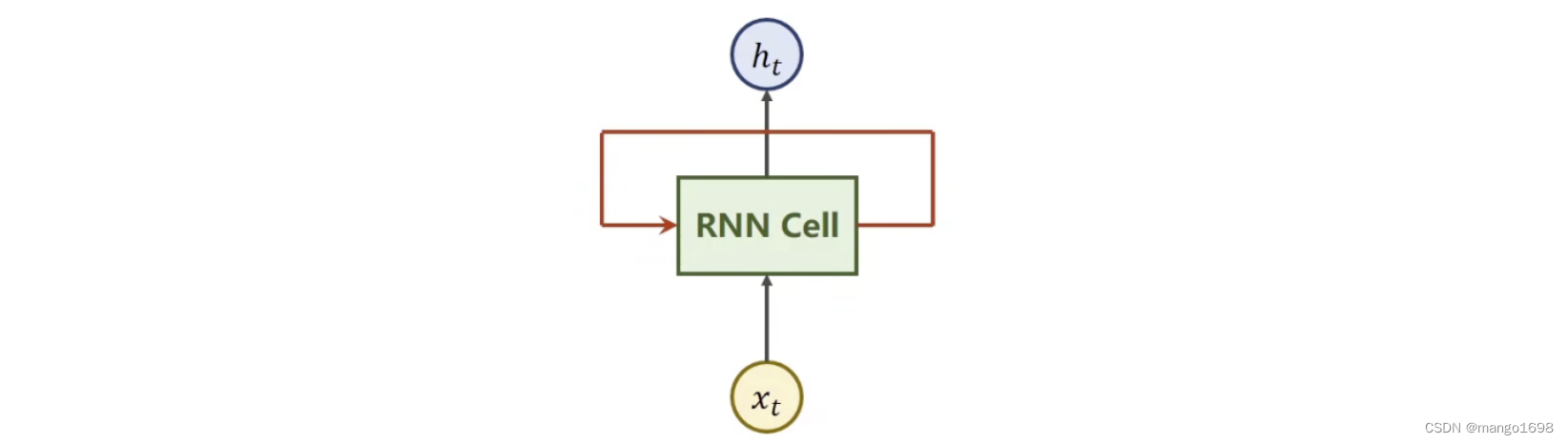
所有的RNN Cell使用的是同一个线性层,就是拿同一个线性层反复的参与运算。
用伪代码实现该过程:
h = torch.zeros(...)
line = Liner()
for x in X:
h = line(x,h)
RNN详细计算过程
输入维度:input_size
隐层维度:hidden_size
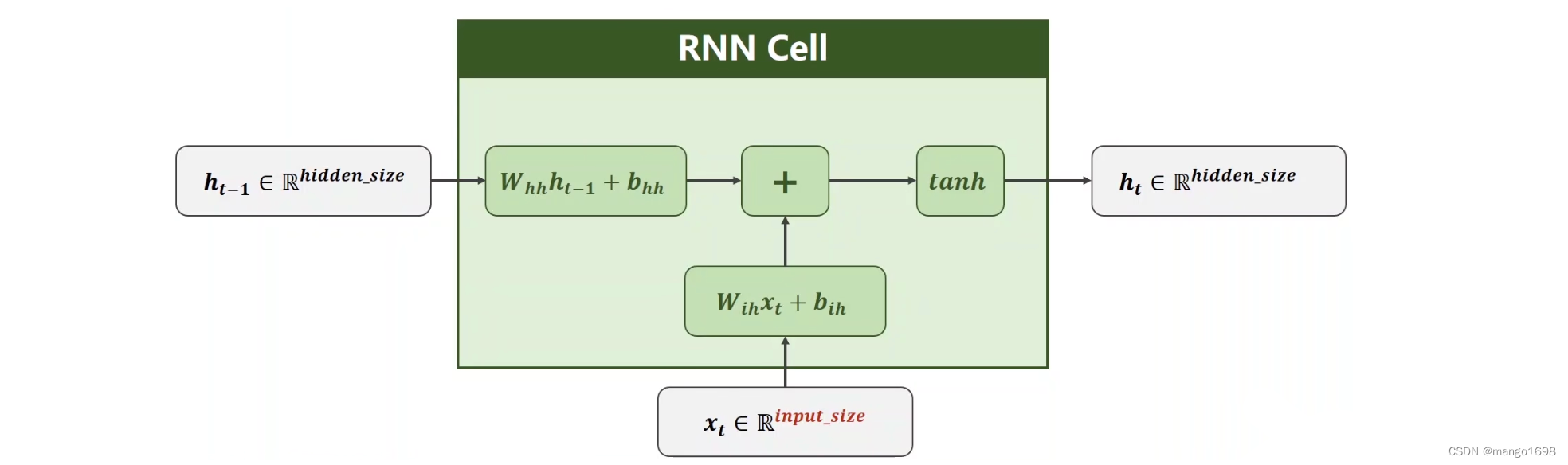
输入先进行线性变换,将输入维度变为隐层维度。所以, W i h W_{ih} Wih的维度应该为 h i d d e n _ s i z e × i n p u t _ s i z e hidden\_size\times input\_size hidden_size×input_size, W h h W_{hh} Whh的维度为 h i d d e n _ s i z e × h i d d e n _ s i z e hidden\_size\times hidden\_size hidden_size×hidden_size。
W h h h t − 1 + b h h W_{hh}h_{t-1}+b_{hh} Whhht−1+bhh的输入应该是一个hidden_size的向量。 W i h x t + b i h W_{ih}x_t+b_{ih} Wihxt+bih的输出是一个hidden_size的向量。
然后将这两个向量直接相加,就把信息融合起来了。
信息融合后,就进行一次激活,使用激活函数为 t a n h tanh tanh函数。( − 1 < t a n h ( x ) < 1 -1<tanh(x)<1 −1<tanh(x)<1)。输出的结果就为 h t h_t ht,这一层隐层的输出。
其实,对于两个线性层
W
h
h
h
t
−
1
+
b
h
h
W_{hh}h_{t-1}+b_{hh}
Whhht−1+bhh和
W
i
h
x
t
+
b
i
h
W_{ih}x_t+b_{ih}
Wihxt+bih,这两个运算可以拼在一起,如(简写)
W
1
h
+
W
2
x
=
(
W
1
,
W
2
)
(
h
x
)
W_1h+W_2x = (W_1,W_2){h \choose x}
W1h+W2x=(W1,W2)(xh)
使用Pytorch构造RNN
两种方式:
- 自己制作RNN Cell,自己写一个处理序列的循环
- 直接使用pytorch提供的RNN
RNN Cell使用
cell = torch.nn.RNNCell(input_size=input_size,hidden_size=hidden_size)
我们定义了rnn cell,我们在调用时,要传入当前这一时刻的输入以及当前的hidden,然后输出一个hidden。
hidden = cell(input,hidden)
我们需要重点关注输入的维度和隐层的维度。
input:shape(batch, input_size)
(输入)hidden:shape(batch, hidden_size)
(输出)hidden:shape(batch, hidden_size)
dataset.shape = (seqLen,batchSize,inputSize)
代码实现,使用RNN Cell
import torch
from torch import nn
batch_size = 64
seq_len = 3
input_size = 4
hidden_size = 2
cell = nn.RNNCell(input_size,hidden_size)
dataset = torch.randn(seq_len,batch_size,input_size)
hidden = torch.zeros(batch_size,hidden_size)
for idx,input in enumerate(dataset):
print("="*20,idx,"="*20)
print("Input size: ",input.shape)
hidden = cell(input,hidden)
print("outputs size: ",hidden.shape)
print(hidden)
直接使用RNN

import torch
from torch import nn
batch_size = 1
seq_len = 3
input_size = 4
hidden_size = 2
num_layers = 1 # RNN有多少层
inputs = torch.randn(seq_len, batch_size, input_size)
hidden = torch.zeros(batch_size, hidden_size)
cell = nn.RNN(input_size, hidden_size, num_layers=num_layers)
out, hidden = cell(inputs, hidden)
# out:h1,h2,...,hn
# hidden:hn

使用RNN,需要确定:
- 批量大小
- 序列长度
- 输入维度,输出维度
- 需要几层的RNN
batch_size=1:相当于只有一句话
seqsize=3:相当于每句话有三个单词
input_size=4:相当于每个单词有4个特征
有10个样本数据,每个样本数据包含3天的天气数据,然后每天的天气的数据有10个特征。
就是seq_size=3,batch_size=10,input_size=10
seq_size=3:每个样本是一个包含3个时间步(3天)的序列。batch_size=10:在一个训练批次中,模型将同时处理10个不同的样本。input_size=10:每个时间步(每天)的输入特征有10维。
numLayers:多层RNN

batch_first属性:如果设置为True·,则需要将batch_size设置为第一个参数。

例子
“hello” –>“oholo”

首先,我们要将输入的这些字符进行向量化,用向量进行表示。
根据字符构造一个词典,给每个字符分配一个索引。

得到索引之后,根据词典,把每一个词变成相应的索引。
使用on-hot,将此转为向量:

比如h的索引为1,那么向量中,只有第二个数字(索引0,1,…)的值设为1,其他都为0。
然后将独热向量作为RNN的序列的输入。输出为长度为4的向量,表示4个字符对应的值,然后接一个交叉熵损失函数。(多分类问题)

训练部分代码
使用RNN Cell
for epoch in range(15):
loss = 0
optimizer.zero_grad()
hidden = net.init_hidden()
print('Predicted string: ',end='')
for input,label in zip(inputs,labels):
hidden = net(input,hidden)
loss += criterion(hidden,label)
_,idx = hidden.max(dim=1)
print(idx2char[idx.item()],end='')
loss.backward()
optimizer.step()
print(', Epoch [%d/15] loss=%.4f'%(epoch+1,loss.item()))
使用RNN
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters(),lr = 0.05)
for epoch in range(15):
optimizer.zero_grad()
outputs = net(inputs)
loss = criterion(outpus,labels)
loss.backward()
optimizer.step()
_,idx = outpus.max(dim=1)
idx = idx.data.numpy()
print('Predicted: ',''.join([idx2char[x] for x in idx]),end='')
print(', Epoch [%d/15] loss=%.3f'%(epoch+1,loss.item()))
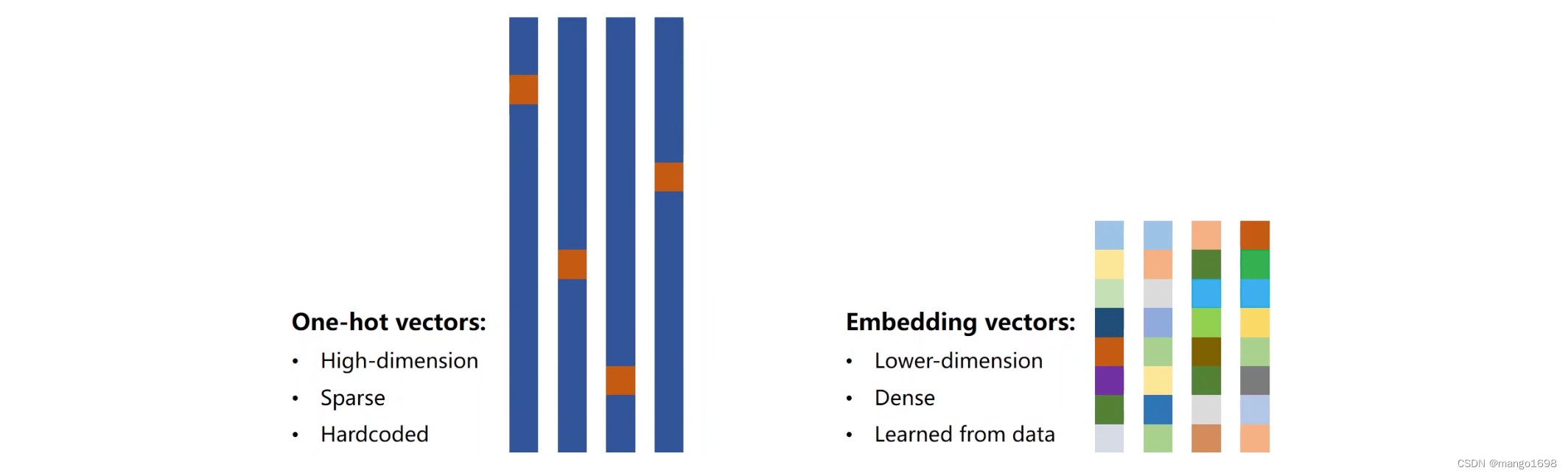
ont-hot字/词编码:
- 独热向量维度太高
- 向量过于稀疏
- 硬编码
所以,我们想找到一种低维、稠密、通过学习得到的方法,来建立词和向量之间的关系:一种流行的方法为:Embedding(嵌入层)。
Embedding:把一个高维的、稀疏的样本映射到一个稠密的、低位的空间里面。(数据降维)
假设,原来的输入一共有4个维度,也就是独热向量是4维的。
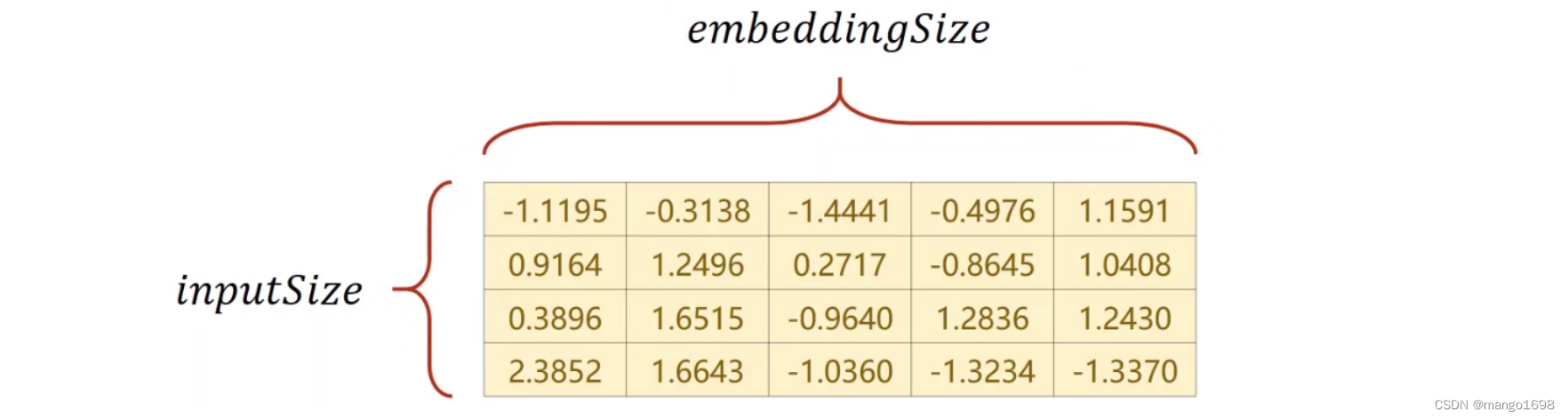
假设嵌入层是5的,从4维转换为5维,就构建上图这种的矩阵。可以在里面进行查询。比如输入的是2,就是指第2个字符,在表里面找到第二行(索引:2),把向量输出。

有了Embedding,网络就可以变为:

在RNN Cell之上我们又连了一层线性层,因为隐层输出必须和分类的数量一致,但是有时候不一致,就再接一个线性层解决该问题。
LSTM 长短期记忆网络

RNN网络联系
根据名字,对其不同的语言进行分类,如下
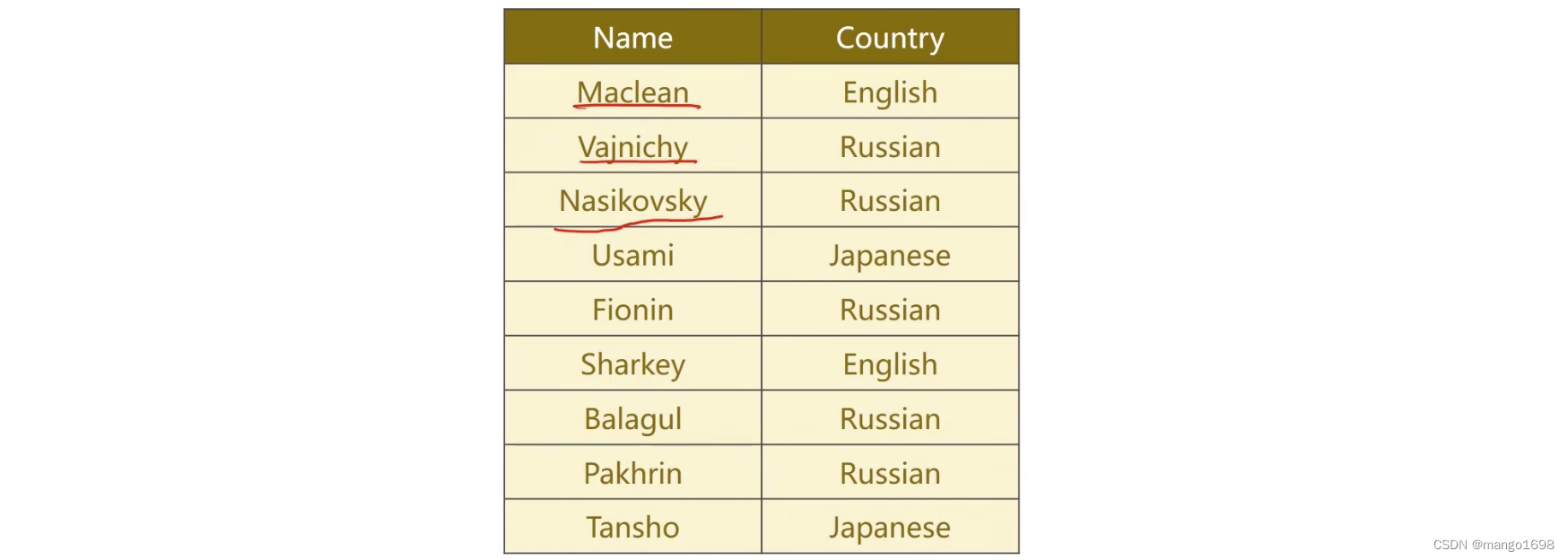
网络结构:


输入为名字,输出为相应的国家。
输入x首先经过嵌入层,然后GRU Layer,然后通过线性层变成想要的输出结果的维度。(GRU是简化的LSTM)
要先将名字转为一个序列

然后对序列做词典,因为这里都是英文字符,我们可以用ASCII码表(0~127)作为字典,那么我们将字典长度设置为128,然后去求我们的每一个字符所对应的ASCII码值。

如,第一个名字中的‘M’字符,所对应的为77,意思是指M所对应的为一个独热向量,第77位为1,其他位置全部为0。
存在问题:输入序列的长短不同。解决办法:我们进行padding操作。

对名字信息处理完成后,对国家信息进行处理,将国家名字转为一个分类索引。

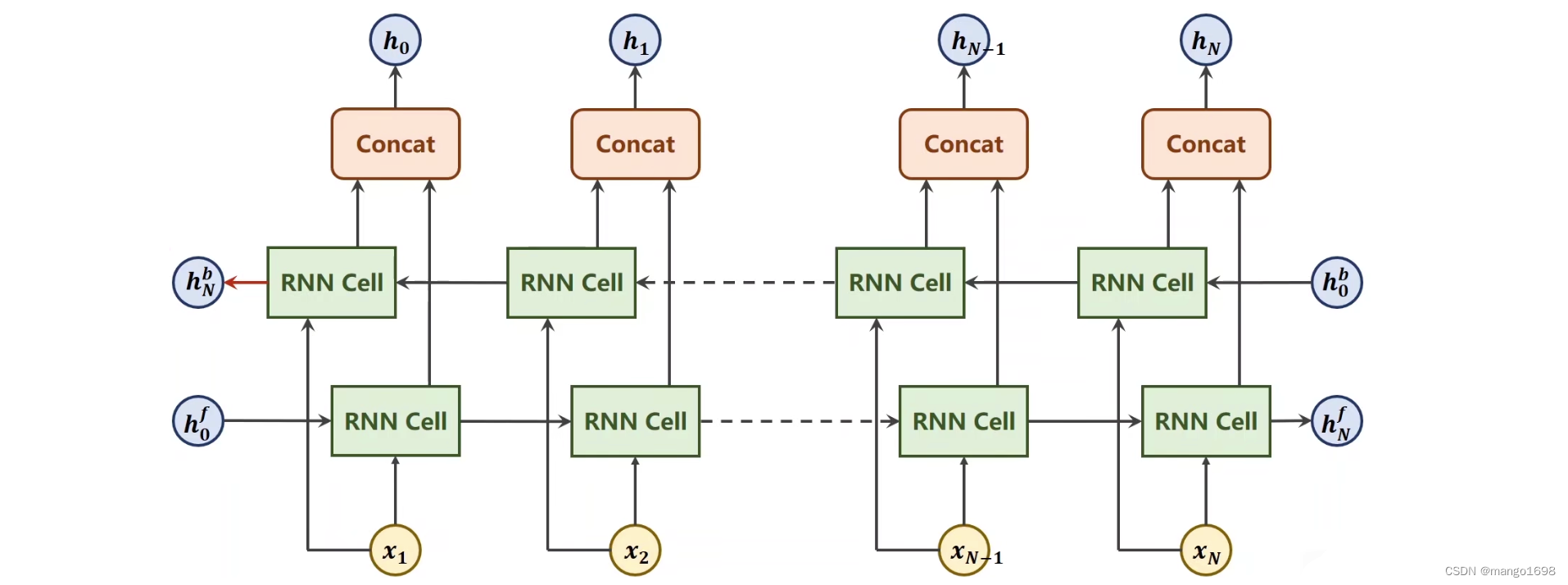
双向循环神经网络