logisitic回归

线性回归目的是找到一条直线（或者超平面）尽可能地接近所有的训练数据点，而对数几率回归的目的是找到一条直线（或者超平面）尽可能地分开两种不同类别的数据点。

对数几率回归感觉更像是一个分类问题。https://blog.csdn.net/amds123/article/details/70243497这篇博客中·已经讲的很好了，分类问题的结果是0或1。而对于logistic回归，我们不再要求直接给出分类结果，而是通过要求“分类结果为1的概率”进而得到分类结果，而概率属于[0,1]。

下面就看下公式的推导。按照sigmoid函数的形式作为正类的概率。下面是sigmoid函数

                                      

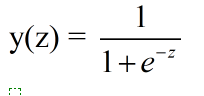
 这个函数的图像是这样的

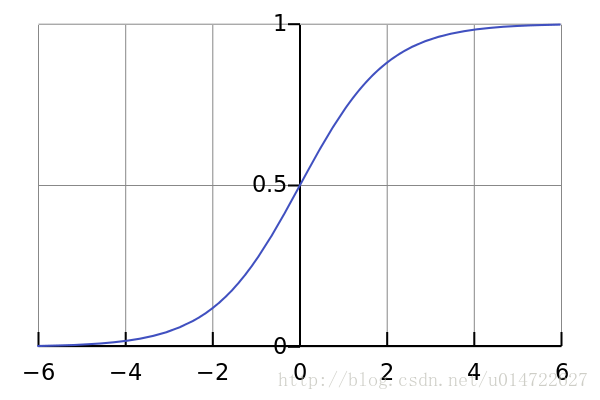
接下来我们只要做出广义上的线性回归， 

 

接下来的我们可以从最大熵模型中推导，最大熵模型为

 

                                          

对于二分类问题

                                   

 

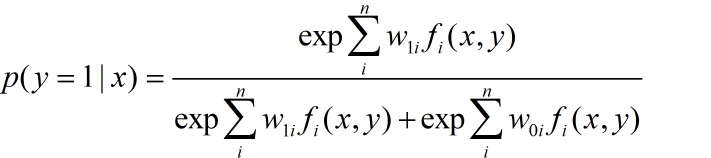
上下同除分子，再另wi  = w1i - w0i就可以得到下面的式子

 

                                    

 

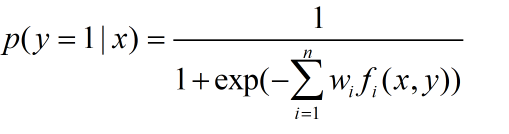
这样正类的概率为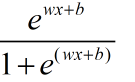，反类的概率为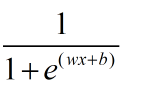这里我们可以令，遵从伯努利分布，我们可以得到概率分布函数

 

                              

 

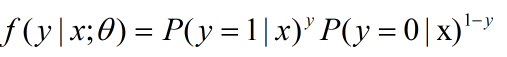
用极大似然估计法得到似然函数

 

                                  

 

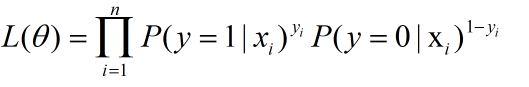
取对数就可以得到：

  

                              

                              

 

 

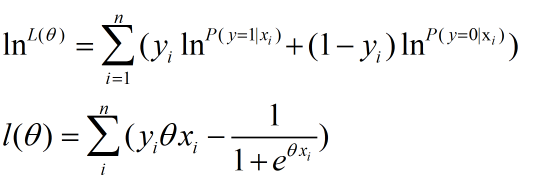
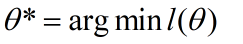
接下来我们可以用梯度下降法求出合适的值