R语言基础知识学习（五）：R中的线性回归分析

在R中线性回归分析的函数是lm()。

（1）一元线性回归

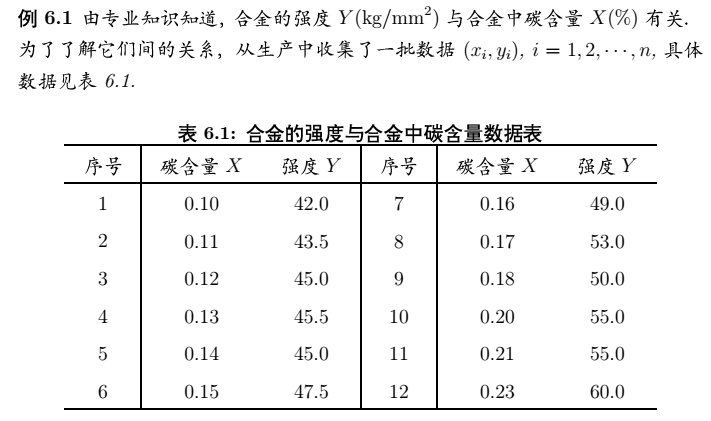
我们可以根据以上数据来分析合金的强度是否与碳含量有关系。

首用以下命令把数据读取到R中：

x <- c(seq(0.10,0.18,by = 0.01),0.20,0.21,0.23)
y <- c(42.0,43.5,45.0,45.5,45.0,47.5,49.0,53.0,50.0,55.0,55.0,60.0)
plot(x,y)

通过画图得到想x,y两个变量之间存在某种线性关系

所以，就可以用lm()函数来拟合直线，通过回归函数lm()得到如下结果：

lm.sol <- lm(y~1+x)  ##lm()函数返回拟合结果的对象，可以用summary()函数查看其内容。
summary(lm.sol)

回归结果：

Call:
lm(formula = y ~ 1 + x)

Residuals:
Min 1Q Median 3Q Max
-2.0431 -0.7056 0.1694 0.6633 2.2653

Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 28.493 1.580 18.04 5.88e-09 ***
  x           130.835 9.683 13.51 9.50e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.319 on 10 degrees of freedom
Multiple R-squared: 0.9481, Adjusted R-squared: 0.9429
F-statistic: 182.6 on 1 and 10 DF, p-value: 9.505e-08

结果分析：

其中，两个回归系数分别是28.493和130.835，结果里面还有t值，以及两个P值，P值越小，回归效果越显著，并且后面星级越高。

倒数第二行R-squared数字越接近于1，回归效果越好。

所以，本例回归分析效果显著，回归直线为：y=28.493+130.835x。

做完回归分析之后还可以进行做预测，也就是说给定一个x值，可以求出Y值的概率为0.95的相应区间。在R中可以用predict()函数实现：

> new <- data.frame(x = 0.16)     ##注意，一个值也要写出数据框的形式。
> lm.pred <- predict(lm.sol,new,interval = "prediction",level = 0.95)   ##加上interval = "prediction"，表示同时给出相应的预测区间。
> lm.pred
　　　　fit          lwr 　　 upr
1  49.42639 46.36621 52.48657

 

 （2）多元线性回归

 

首先把数据读取到R中：

> x1 <- c(76.0,91.5,85.5,82.5,79.0,80.5,74.5,79.0,85.0,76.5,82.0,95.0,92.5)
> x2 <- c(50,20,20,30,30,50,60,50,40,55,40,40,20)
> y <- c(120,141,124,126,117,125,123,125,132,123,132,155,147)
> mydata <- data.frame(x1,x2,y)

做线性回归：

> lm.sol <- lm(y ~ x1 + x2,data = mydata)
> summary(lm.sol)

结果：

Call:
lm(formula = y ~ x1 + x2, data = mydata)

Residuals:
Min 1Q Median 3Q Max
-4.0404 -1.0183 0.4640 0.6908 4.3274

Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -62.96336 16.99976 -3.704 0.004083 **
x1 2.13656 0.17534 12.185 2.53e-07 ***
x2 0.40022 0.08321 4.810 0.000713 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.854 on 10 degrees of freedom
Multiple R-squared: 0.9461, Adjusted R-squared: 0.9354
F-statistic: 87.84 on 2 and 10 DF, p-value: 4.531e-07

从以上结果来看，回归系数和回归方程的检验都是显著的，所以回归方程为：y=-62.96366+2.13656x1+0.40022x2

 与一元回归一样，也可以用predict()函数做预测：

下面来预测以为体重80KG，年龄40岁的男子的血压:

> new <- data.frame(x1 = 80,x2 = 60)
> lm.pred <- predict(lm.sol,new ,interval = "prediction", level = 0.95)
> lm.pred
　　　　fit 　    lwr　　    upr
1 131.9743 124.6389 139.3096