STL源码剖析---红黑树原理详解

红黑树概述

红黑树都是在进行插入和删除时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。红黑树追求的时局部平衡而不是AVL树中的非常严格的平衡。

所谓红黑树，不仅是一个二叉搜索树，而且必须满足一下规则：

     1、每个节点不是红色就是黑色。
     2、根节点为黑色。
     3、如果节点为红色，其子节点必须为黑色。
     4、任意一个节点到到NULL（树尾端）的任何路径，所含之黑色节点数必须相同。

 上面的这些约束保证了这个树大致上是平衡的，这也决定了红黑树的插入、删除、查询等操作是比较快速的。 根据规则4，新增节点必须为红色；根据规则3，新增节点之父节点必须为黑色。当新增节点根据二叉搜索树的规则到达其插入点时，却未能符合上述条件时，就必须调整颜色并旋转树形，如下图：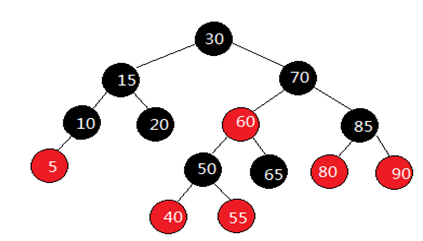

 假设我们为上图分别插入节点3、8、35、75，根据二叉搜索树的规则，插入这四个节点后，我们会发现它们都破坏了红黑树的规则，因此我们必须调整树形，也就是旋转树形并改变节点的颜色。

红黑树上结点的插入

    在讨论红黑树的插入操作之前必须要明白，任何一个即将插入的新结点的初始颜色都为红色。这一点很容易理解，因为插入黑点会增加某条路径上黑结点的数目，从而导致整棵树黑高度的不平衡。但如果新结点的父结点为红色时（如下图所示），将会违反红黑树的性质：一条路径上不能出现相邻的两个红色结点。这时就需要通过一系列操作来使红黑树保持平衡。

最深点---失去平衡最深的节点

分四种情况插入：

• 外侧插入（左左）且根节点的右节点为黑色  解法：先对根节点单旋转下移，后改变根节点和根节点左节点的颜色‘
• 内侧插入（左右）且根节点的右节点为黑色  解法：第一次，将插入点上移操作，并改变插入点和最深节点的颜色；第二次，单旋转根节点下移（不必更改颜色），即将最深点下移
• 外侧插入（左左）且根节点的右节点为红色 解法：现对根节点单旋转下移，后只改变插入节点的颜色
• 外侧插入（左左左）且根节点的右节点为NULL  解法：先对根节点的左节点单旋转下移，并改变插入节点的颜色；