20202303 实验九《数据结构与面向对象程序设计》实验报告
# 20202303 2021-2022-1 《数据结构与面向对象程序设计》实验九报告
课程:《程序设计与数据结构》
班级: 2023
姓名: 马澜
学号:20202303
实验教师:王志强
实验日期:2021年12月20日
必修/选修: 必修
## 1.实验内容
-
(1) 初始化:根据屏幕提示(例如:输入1为无向图,输入2为有向图)初始化无向图和有向图(可用邻接矩阵,也可用邻接表),图需要自己定义(顶点个数、边个数,建议先在草稿纸上画出图,然后再输入顶点和边数)(2分)
(2) 图的遍历:完成有向图和无向图的遍历(深度和广度优先遍历)(4分)
(3) 完成有向图的拓扑排序,并输出拓扑排序序列或者输出该图存在环(3分)
(4) 完成无向图的最小生成树(Prim算法或Kruscal算法均可),并输出(3分)
(5) 完成有向图的单源最短路径求解(迪杰斯特拉算法)(3分)PS:本题12分。目前没有明确指明图的顶点和连通边,如果雷同或抄袭,本次实验0分。
实验报告中要根据所编写的代码解释图的相关算法
## 2. 实验过程及结果
(1)初始化:根据屏幕提示(例如:输入1为无向图,输入2为有向图)初始化无向图和有向图(可用邻接矩阵,也可用邻接表),图需要自己定义(顶点个数、边个数,建议先在草稿纸上画出图,然后再输入顶点和边数)
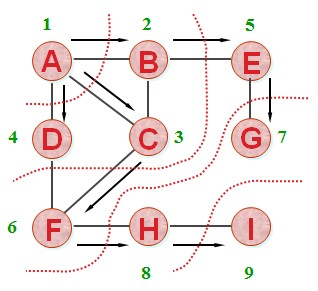
首先先画出有向图和无向图,如下:
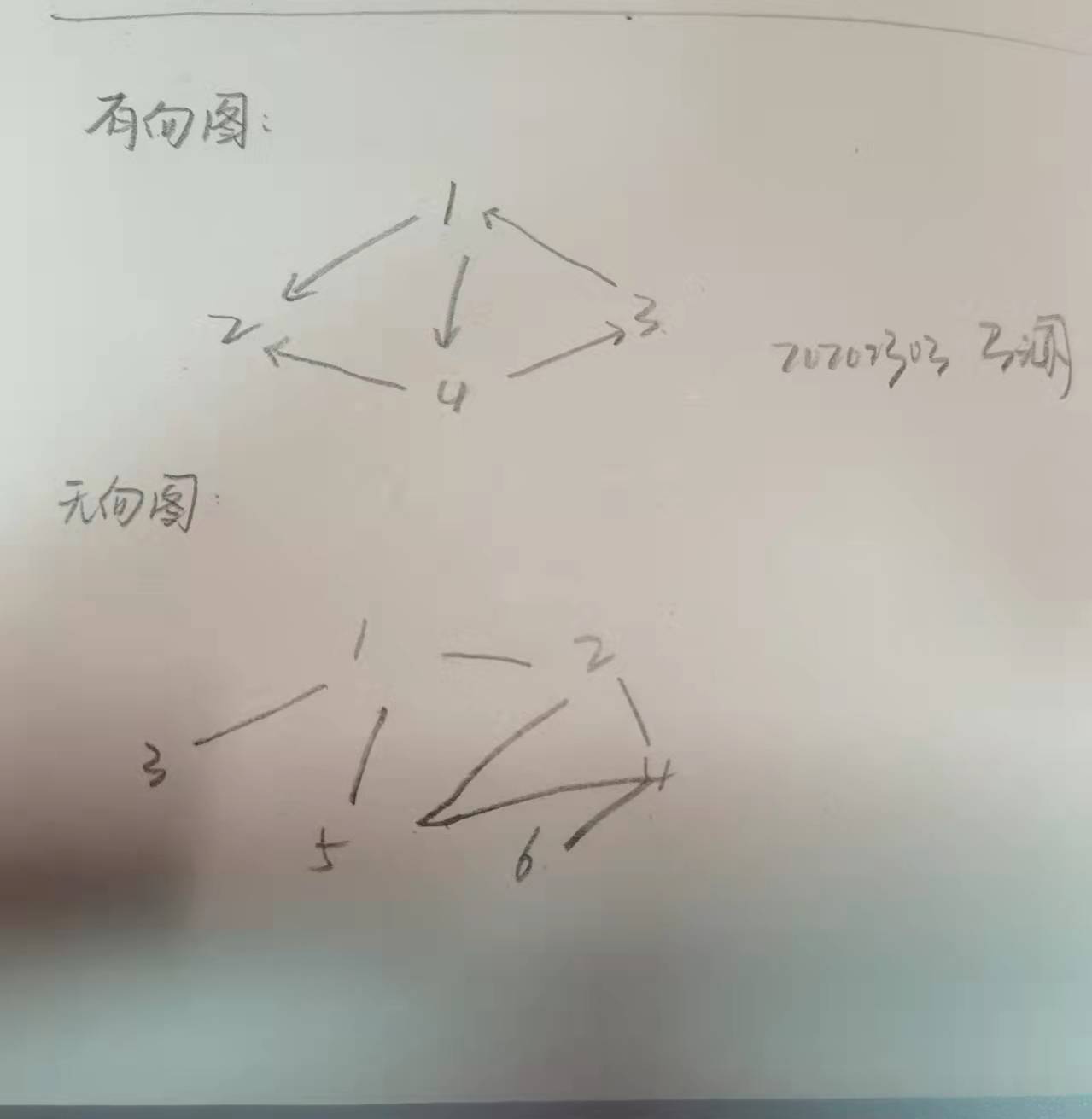
通过自定义结点、边的个数与对应的关系,构造出有向图和无向图的邻接表,接下来是代码:
有向图,无向图的建立算法:
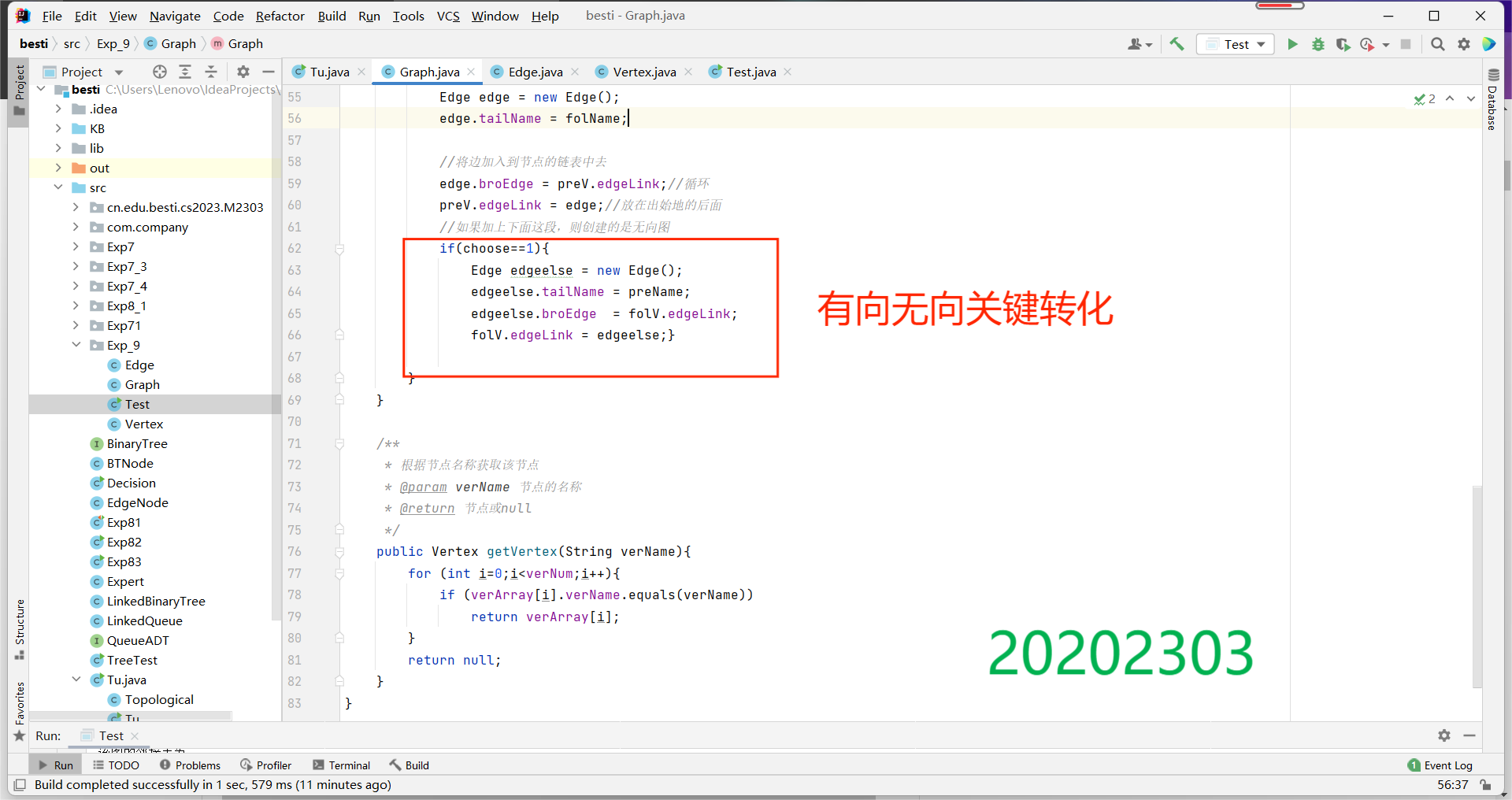
测试(构建)结果
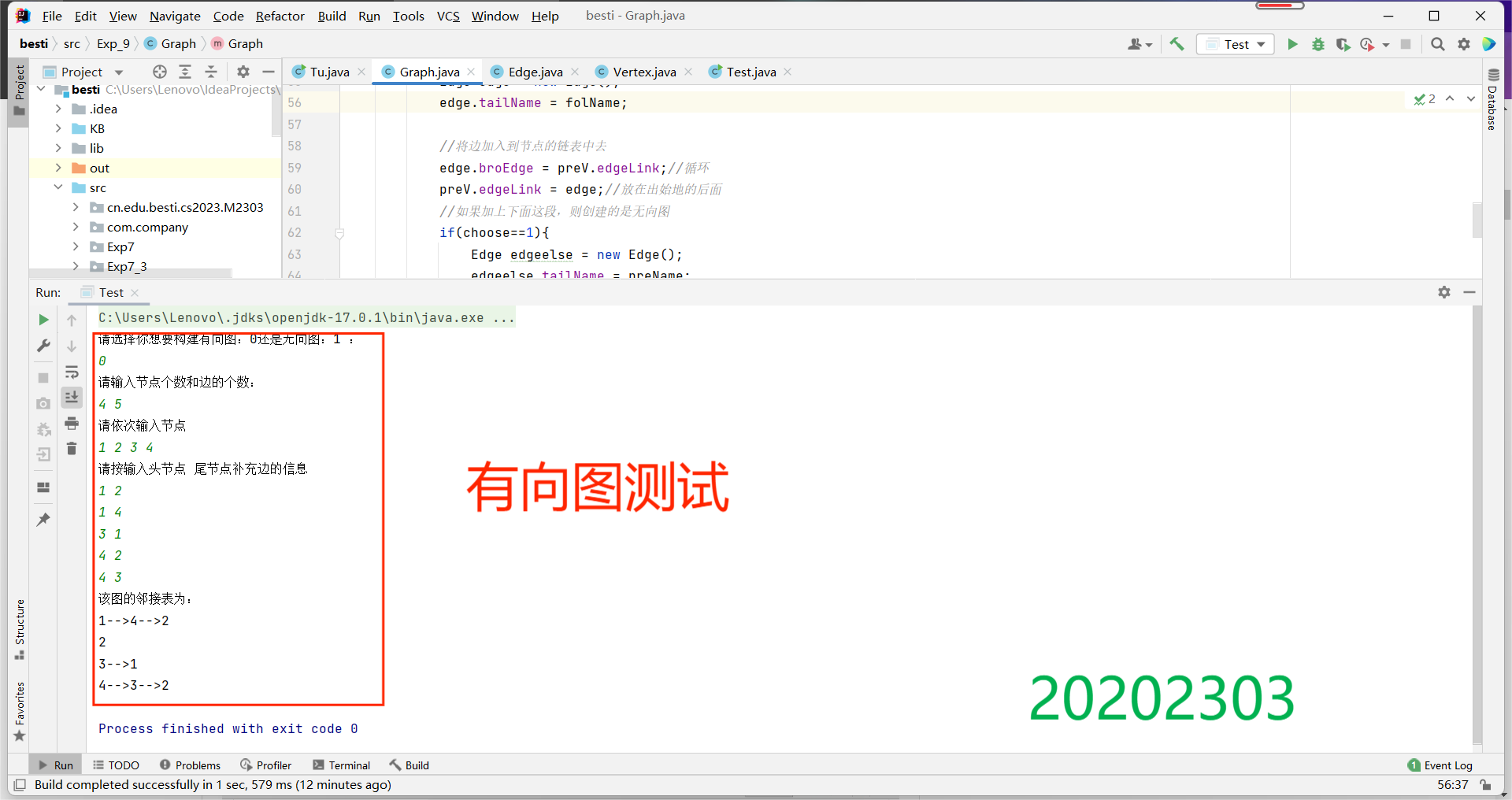
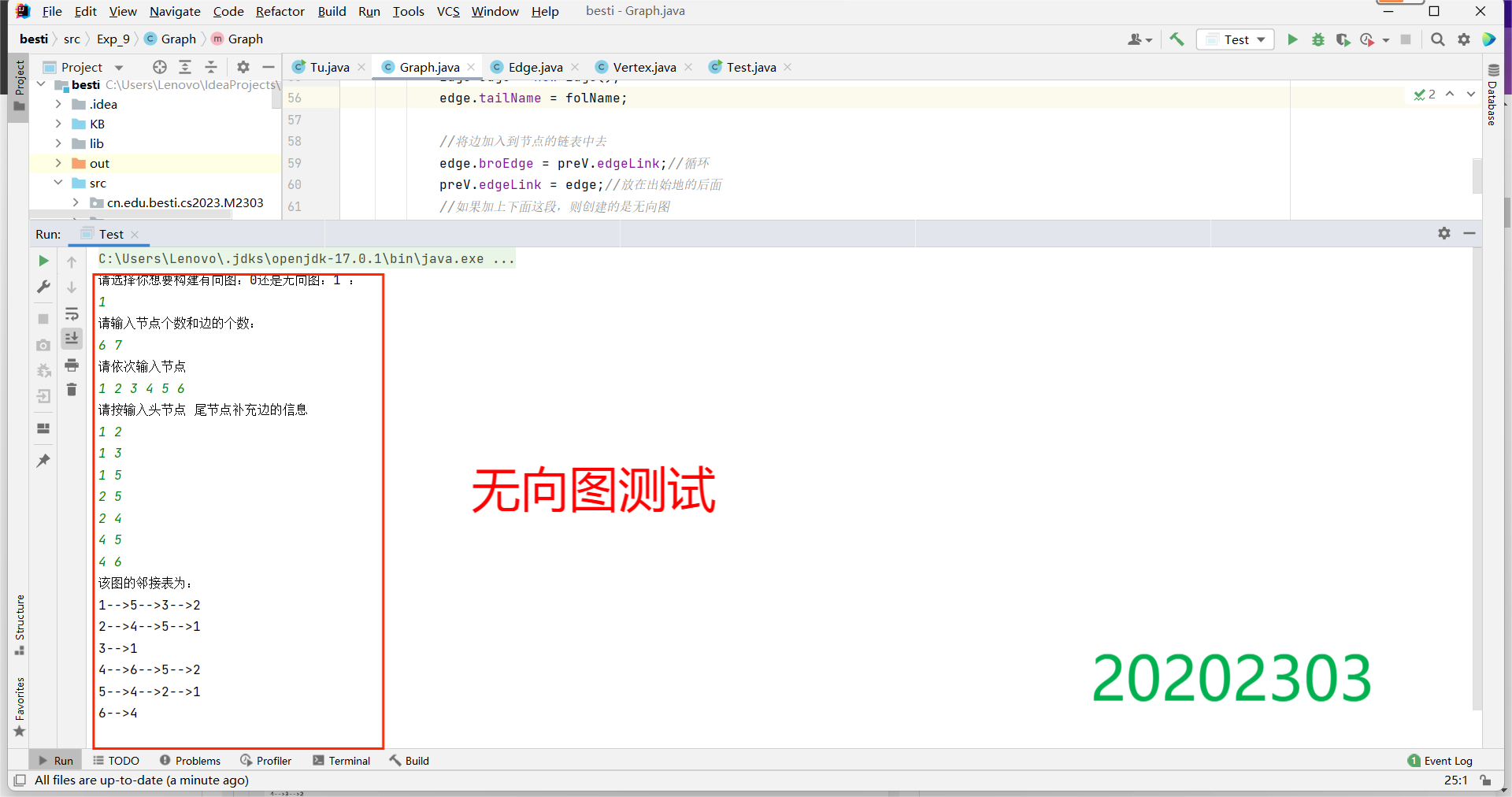
(2)图的遍历:完成有向图和无向图的遍历(深度和广度优先遍历)
这个程序主要是将自己所构造的图分别用深度优先遍历与广度优先遍历两种方法遍历一遍,然后接下来是对两种遍历的简单介绍:
- 深度遍历的大致实现思路是:把根节点压入栈中。每次从栈中弹出一个元素,搜索所有在它下一级的元素,把这些元素压入栈中。并把这个元素记为它下一级元素的前驱。找到所要找的元素时结束程序。如果遍历整个树还没有找到,结束程序。
- 广度遍历的大致实现思路是:把根节点放到队列的末尾。每次从队列的头部取出一个元素,查看这个元素所有的下一级元素,把它们放到队列的末尾。并把这个元素记为它下一级元素的前驱。找到所要找的元素时结束程序。如果遍历整个树还没有找到,结束程序。
- 代码示例:
-
//深度优先遍历 public void DFS(String vertexName){ int id=getIdOfVertexName(vertexName); if(id==-1)return; vertexs.get(id).setMarked(true); System.out.print(vertexs.get(id).getName()+" "); List<Vertex> neighbors = getNeighbors(vertexs.get(id)); for(int i=0;i<neighbors.size();i++){ if(!neighbors.get(i).isMarked()){ DFS(neighbors.get(i).getName()); } } } //广度优先遍历 public void BFS(String vertexName){ int startID=getIdOfVertexName(vertexName); if(startID==-1) return; List<Vertex> q=new ArrayList<Vertex>(); q.add(vertexs.get(startID)); vertexs.get(startID).setMarked(true); while(!q.isEmpty()){ Vertex curVertex=q.get(0); q.remove(0); System.out.print(curVertex.getName()+" "); List<Vertex> neighbors = getNeighbors(curVertex); for(int i=0;i<neighbors.size();i++){ if(!neighbors.get(i).isMarked()){ neighbors.get(i).setMarked(true); q.add(neighbors.get(i)); } } } } -
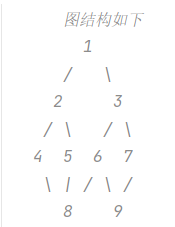
示意图如下: ![]()
- 构建的图为
![]()
所以构建代码如此下:
测试结果:
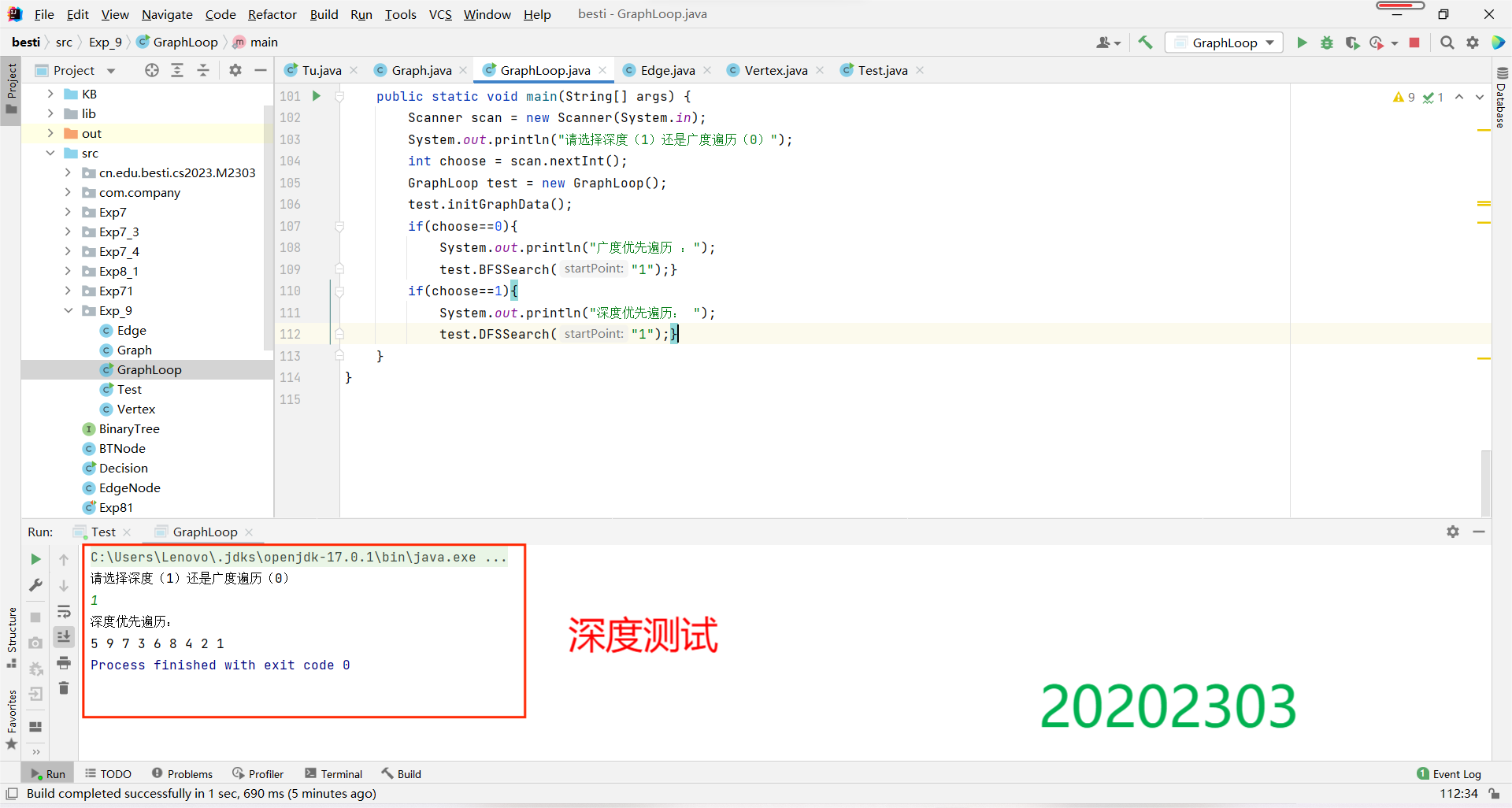
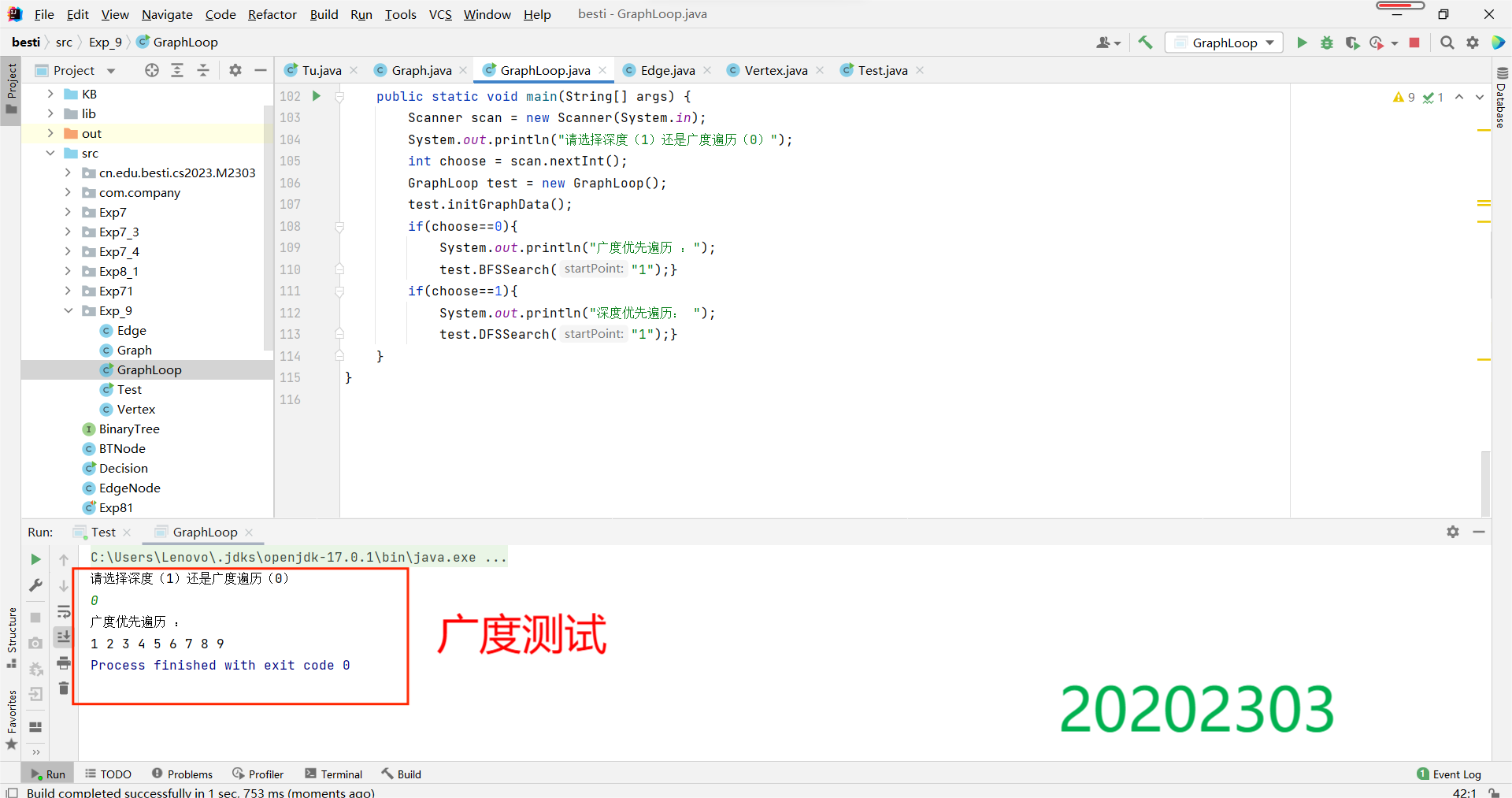
(3)完成有向图的拓扑排序,并输出拓扑排序序列或者输出该图存在环
- 拓扑排序的基本思路是:先选定一个入度为零的结点,删除它和它相连的边,将该结点标记为已访问,同时与该结点相连的入度全部减一。接着,重复进行寻找入度为零结点——标记删除——相连结点入度减一的过程,直到所有结点都已被标记或图中有环。
- 先初始化
startNode = directedGraph.get(startNodeLabel);
if (startNode == null) {
startNode = new Vertex(startNodeLabel);
directedGraph.put(startNodeLabel, startNode);
}
endNode = directedGraph.get(endNodeLabel);
if (endNode == null) {
endNode = new Vertex(endNodeLabel);
directedGraph.put(endNodeLabel, endNode);
}
e = new Edge(endNode);//每读入一行代表一条边
startNode.adjEdges.add(e);//每读入一行数据,起始顶点添加一条边
endNode.inDegree++;//每读入一行数据,终止顶点入度加1
- 判断圆环
Queue<Vertex> queue = new LinkedList<>();// 拓扑排序中用到的栈,也可用队列.
//扫描所有的顶点,将入度为0的顶点入队列
Collection<Vertex> vertexs = directedGraph.values();
for (Vertex vertex : vertexs)
if(vertex.inDegree == 0)
queue.offer(vertex);
while(!queue.isEmpty()){
Vertex v = queue.poll();
System.out.print(v.vertexLabel + " ");
count++;
for (Edge e : v.adjEdges)
if(--e.endVertex.inDegree == 0)
queue.offer(e.endVertex);
}
if(count != directedGraph.size()){
throw new Exception("Graph has circle");
}
测试如下,以(1)中有向图为例;
有环:
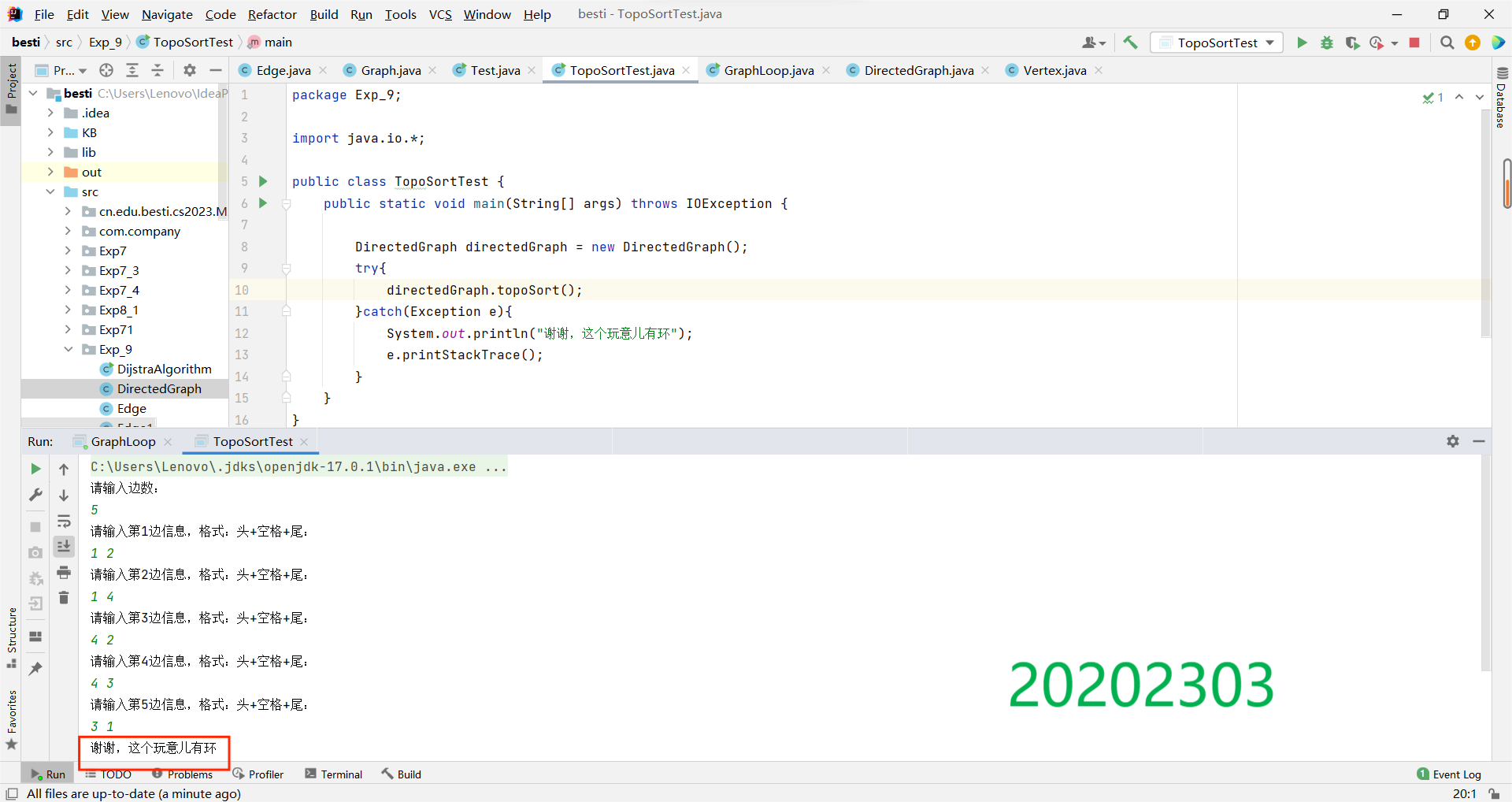
无环(将(1)中4—>3变为3—>4):
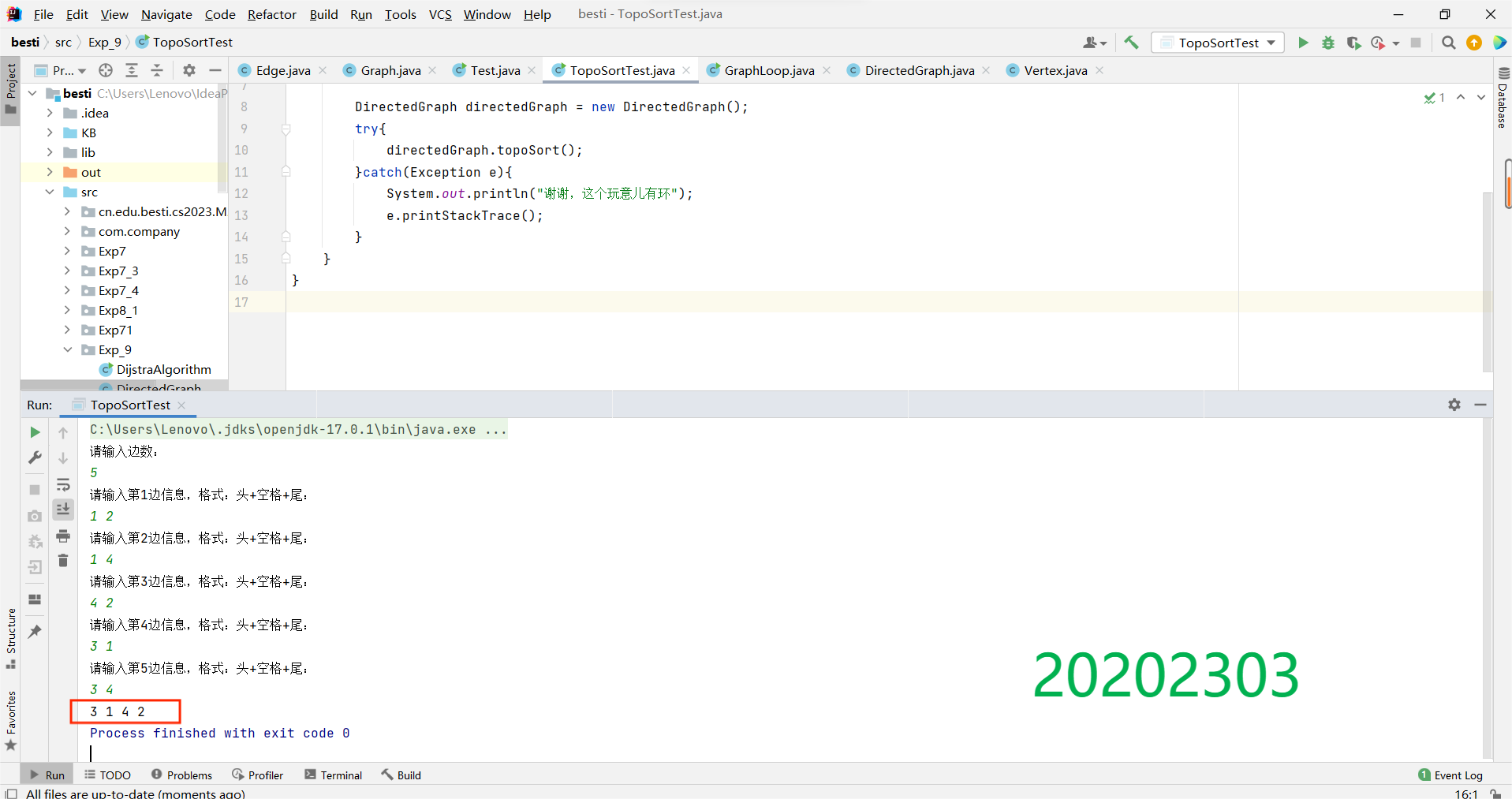
完美!!!!
(4) 完成无向图的最小生成树(Prim算法或Kruscal算法均可),并输出。
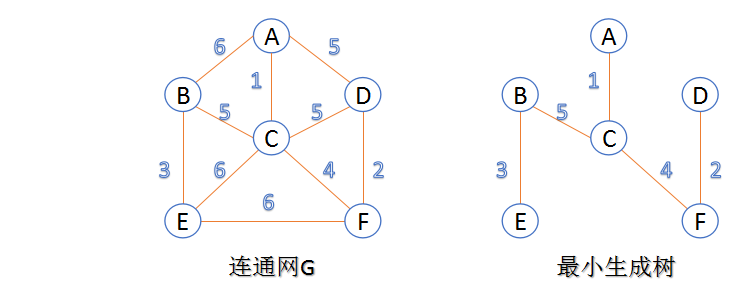
- 最小生成树的构造方法共有两种:Kruskal与Prim算法
![3]()
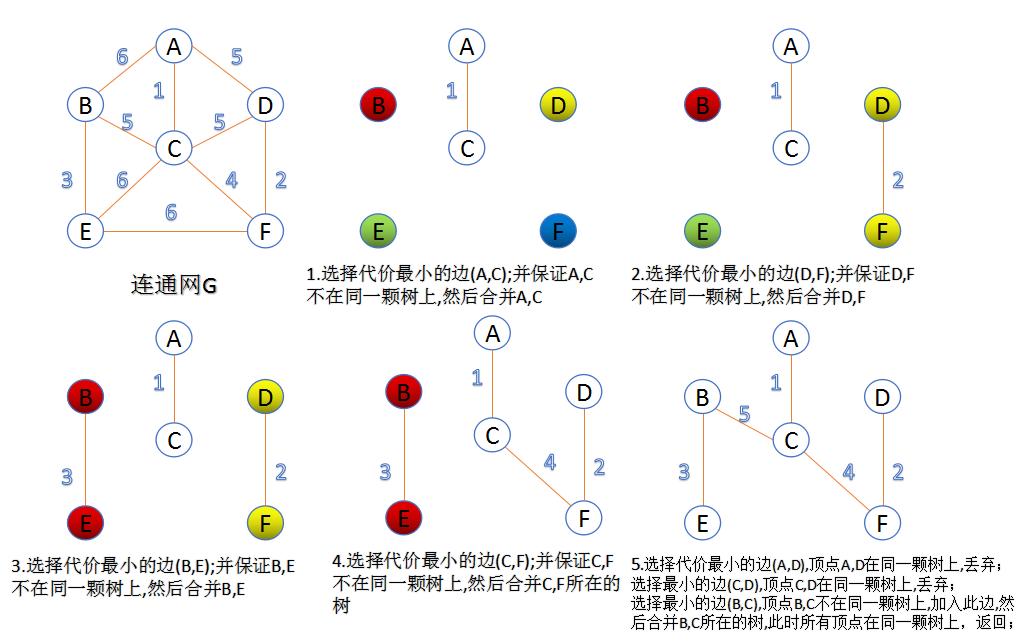
- Kruskal算法基本思路:将权值按从小到大的顺序排列,依次连接,即每一次都连接权值最小的那条边,直到所有结点都在一棵树内或有n-1条边为止
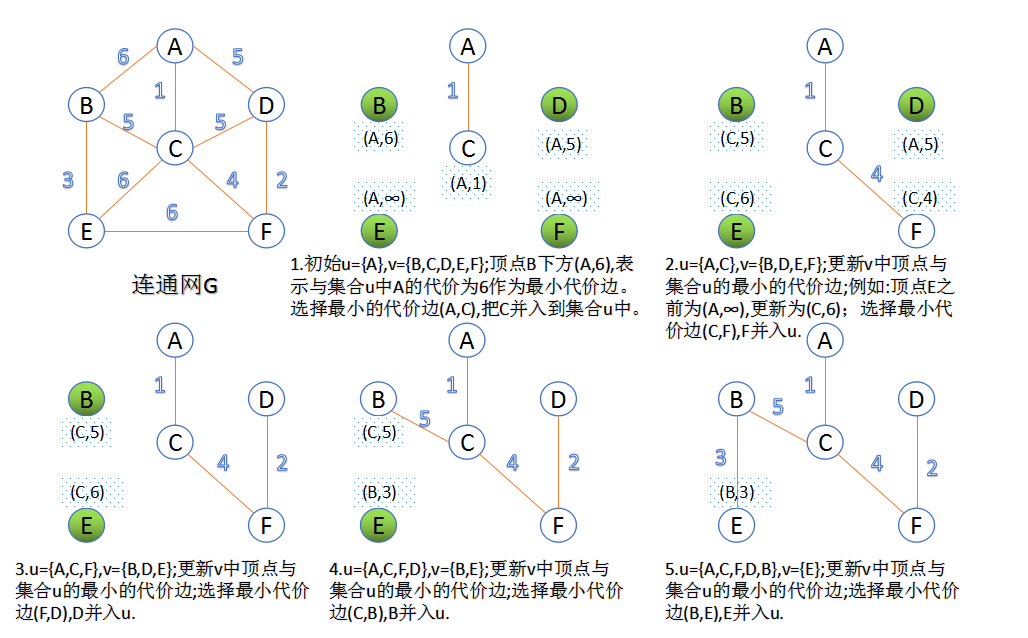
- Prim算法基本思路:从某一特定结点开始,首先选择与其相连的权值最小的边,接着选择与这两个结点相连的权值最小的边,依次进行,每次连接的都是与当前所有结点相连的权值最小的边
![4]()
![5]()
- 我选择Prim算法,建立边并进行对比
public Edge(int i,int j,int w){ this.i=i; this.j=j; this.w=w; } @Override public int compareTo(Object o) { Edge to=(Edge)o; if(this.w>to.w) return 1; else if(this.w==to.w) return 0; else return -1; }
所以先确定一个带权的无向图,如下:
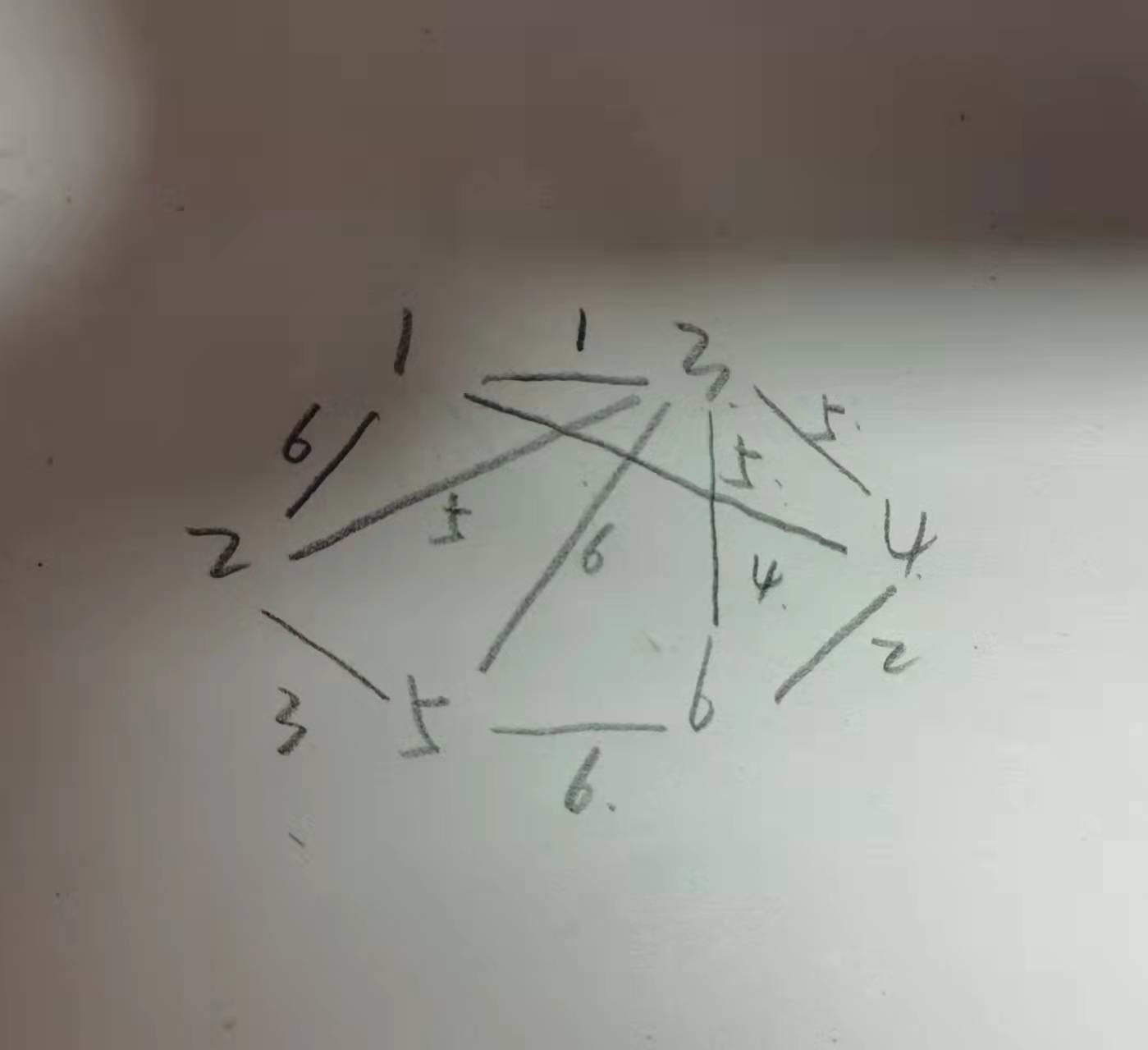
编写为程序形式为:

然后进行测试:
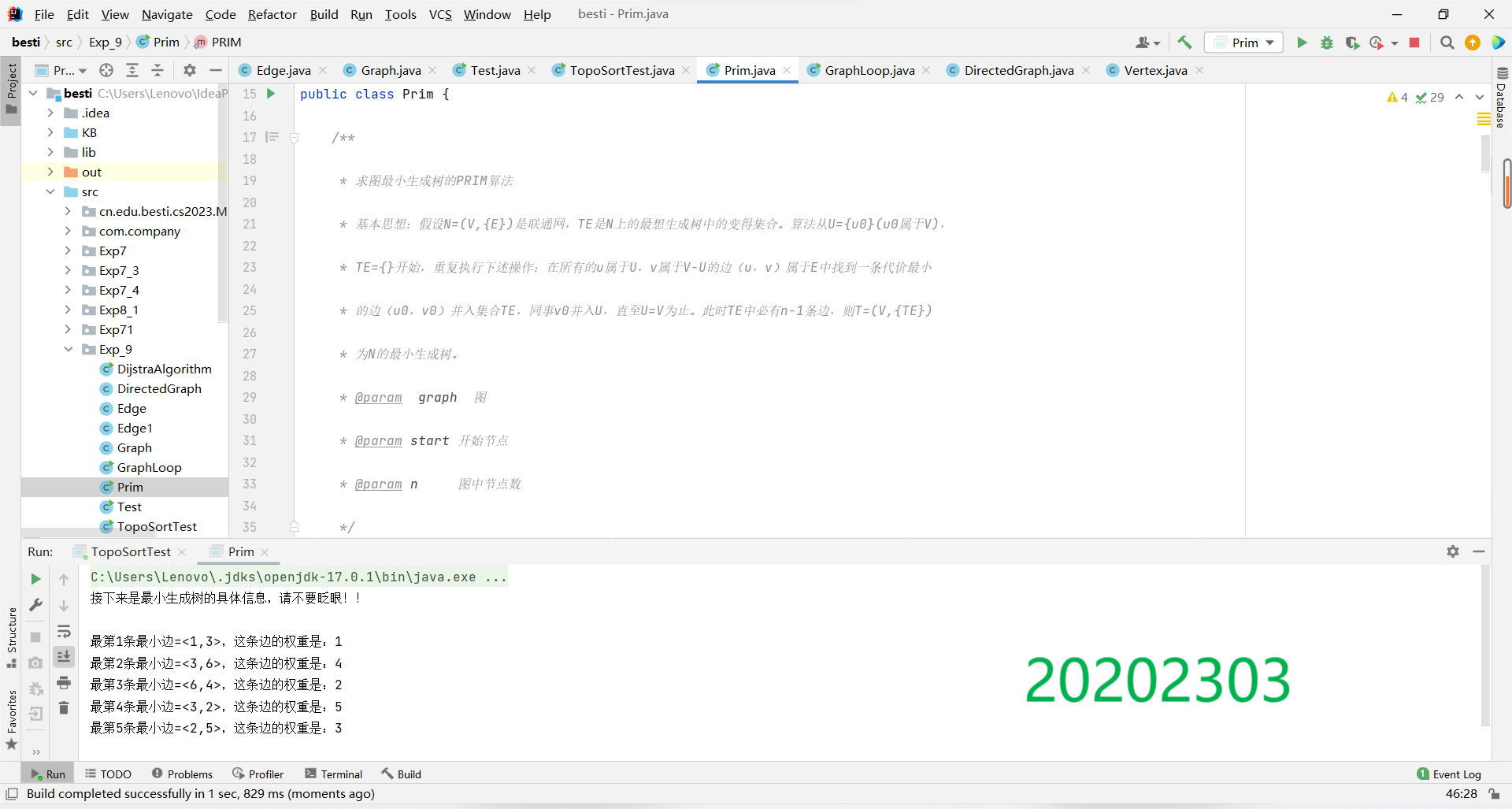
(5)完成有向图的单源最短路径求解(迪杰斯特拉算法)
详解Dijkstra算法
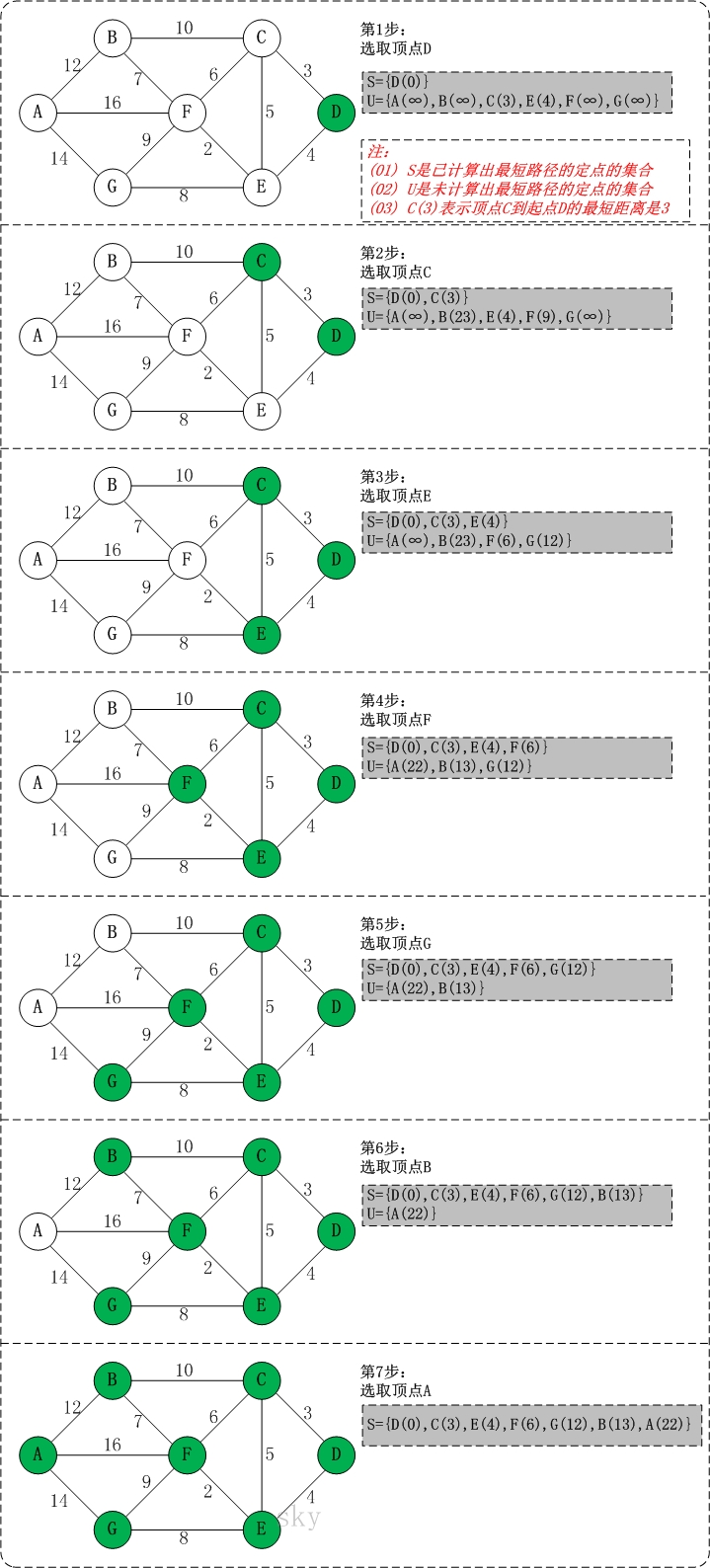
- 初始时,S只包含起点s;U包含除s外的其他顶点,且U中顶点的距离为"起点s到该顶点的距离"[例如,U中顶点v的距离为(s,v)的长度,然后s和v不相邻,则v的距离为∞]
- 从U中选出"距离最短的顶点k",并将顶点k加入到S中;同时,从U中移除顶点k
- 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出最短路径的顶点,从而可以利用k来更新其它顶点的距离;例如,(s,v)的距离可能大于(s,k)+(k,v)的距离
- 重复步骤(2)和(3),直到遍历完所有顶点
![5]()
- 通过迪杰斯特拉(Dijkstra)算法求以vertex[srcIndex]顶点作为源点到其余各顶点的最短路径
public static Info dijkstra(Graph g, int srcIndex) {
if(srcIndex < 0 || srcIndex >= g.vertexNum){
return null;
}
int[] pathSerials = new int[g.vertexNum]; // pathSerials[i]表示从源点到顶点i的最短路径(即若P(srcIndex,j)={V(srcIndex)...Vk...Vs...Vj}是从源点srcIndex到j的最短路径,则有P(srcIndex,j)=P(srcIndex,k)+P(k,s)+P(s,j))
int[] path = new int[g.vertexNum]; // path[i]表示从源点到顶点i(i为vertexs中的索引)的最短路径中顶点i的前驱顶点
int index = 0;
pathSerials[index] = srcIndex; // 源点加入序列中
g.visited[srcIndex] = true; // 源点已在最短路径序列中
Arrays.fill(path, -1); // -1表示顶点没有前驱顶点
int[] distances = new int[g.vertexNum]; // distances[i]表示从源点到顶点i(i为vertexs中的索引)的当前最短路径长度
for (int i = 0; i < g.vertexNum; i++) {
// 初始化distances为其余顶点到源点的权值
distances[i] = g.matrix[srcIndex][i];
}
int minIndex = srcIndex;
while (minIndex != -1) { // 仍有未加入到最短路径序列中的顶点
index++;
for (int i = 0; i < g.vertexNum; i++) {
if (!g.visited[i]) { // 更新仍未加入到最短路径序列中的顶点的从源点到它的值
// 这些仍未加入到最短路径序列中的顶点的distances[i]值为(刚加入的顶点minIndex的distances[minIndex]与minIndex到顶点i之和)与(顶点minIndex刚加入之前源点到i的距离值distances[i])两者之间的较小者
distances[i] = Math.min(distances[i], distances[minIndex] + g.matrix[minIndex][i]);
// 如果当前顶点i的distances[i]值为新加入的顶点minIndex,则顶点i的前驱为minIndex,否则不变
if(distances[i] == distances[minIndex] + g.matrix[minIndex][i] && distances[i] != Integer.MAX_VALUE / 2){ // distances[i] != Integer.MAX_VALUE / 2表示仍不可达,就没有前驱
path[i] = minIndex;
}
}
}
minIndex = indexOf(g, distances); // 选出的最小顶点
if(minIndex == -1){
break;
}
pathSerials[index] = minIndex; // 刚选出的最小顶点加入到最短路径序列中
g.visited[minIndex] = true;
}
return new Info(distances, pathSerials, getPathOfAll(path, pathSerials));
}
- 找到图中仍未加入到最短路径序列顶点集中到源点距离最小的顶点的索引
public static int indexOf(Graph g, int[] distances) {
int min = Integer.MAX_VALUE / 3;
int minIndex = -1; // 当前数组distances剩余元素最小值(-1表示无剩余元素)--剩余元素就是仍未加入到最短路径序列中的顶点
for(int i = 0; i < g.vertexNum; i++){
if(!g.visited[i]){ // 如果i顶点仍未加入到最短路径序列中
if(distances[i] < min){
min = distances[i];
minIndex = i;
}
}
}
return minIndex;
}
- 得到指定顶点i的从源点到顶点i的最短路径(均以顶点集vertexs中索引表示)
public static int[] getPath(int[] path, int i){
Stack<Integer> s = new Stack<Integer>();
s.push(i);
int pre = path[i];
while(pre != -1){
s.push(pre);
pre = path[pre];
}
int size = s.size();
int[] pathOfVertex = new int[size];
while(!s.isEmpty()){
pathOfVertex[size - s.size()] = s.pop();
}
return pathOfVertex;
}
- 最短路径
public static class Info{
private int[] distances; // 源点到各个顶点的最短距离
private int[] pathSerials; // 整个最短路径序列
private ArrayList<int[]> paths; // 源点到各个顶点的确切最短路径序列
public Info(int[] distances, int[] pathSerials, ArrayList<int[]> paths) {
this.distances = distances;
this.pathSerials = pathSerials;
this.paths = paths;
}
}
然后有图如下,然后进行程序编写,将A,B,C,D,E分别作为索引0,1,2,3,4代替进行最小路径寻找,然后测试,结果如下:
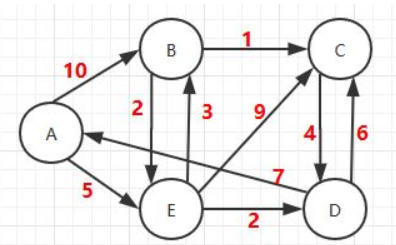
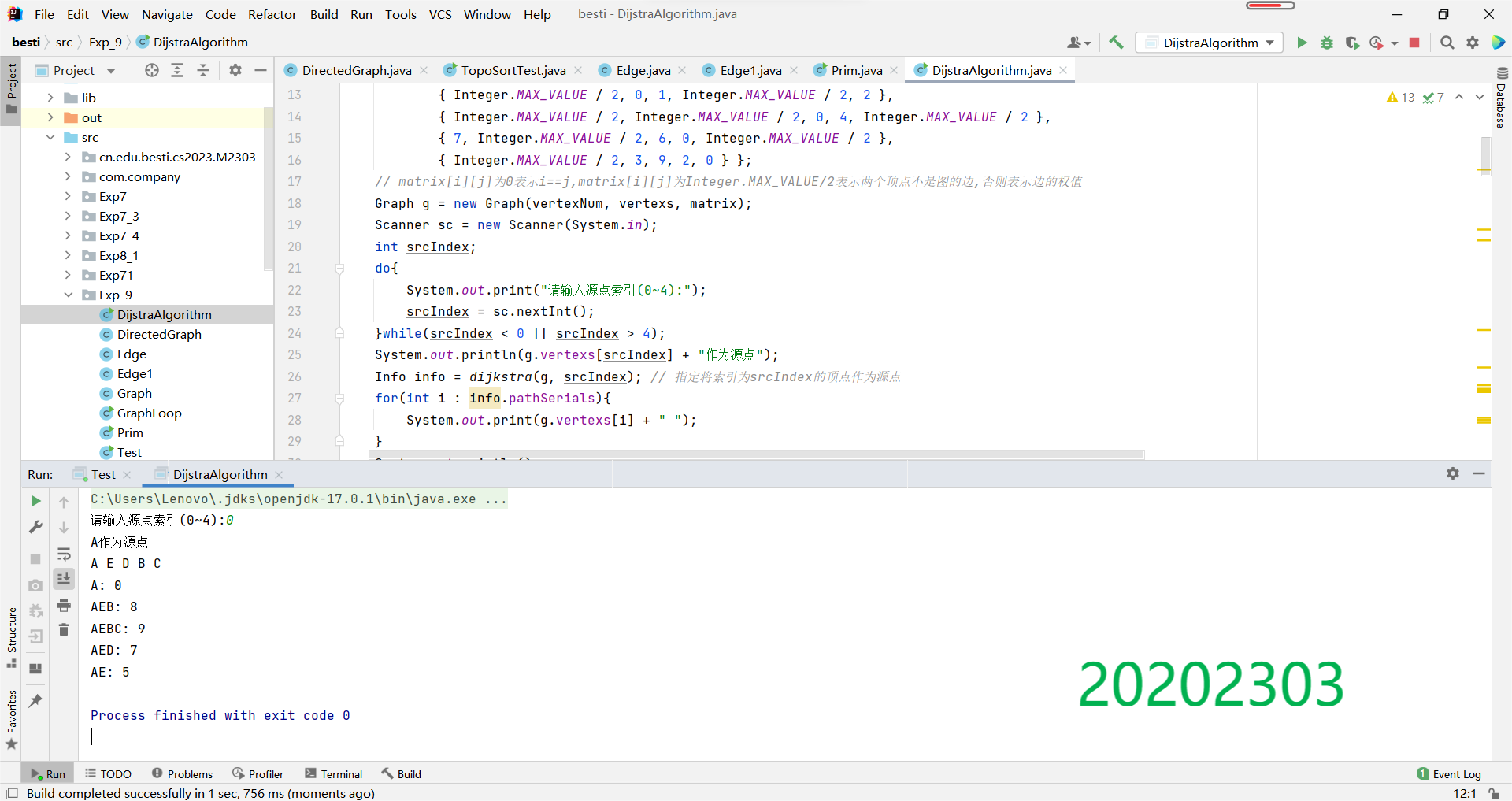
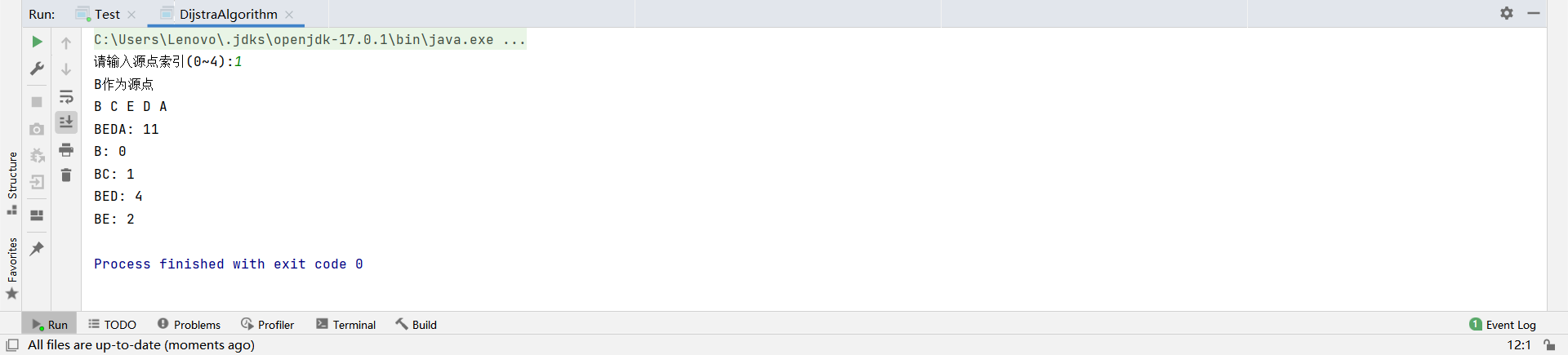
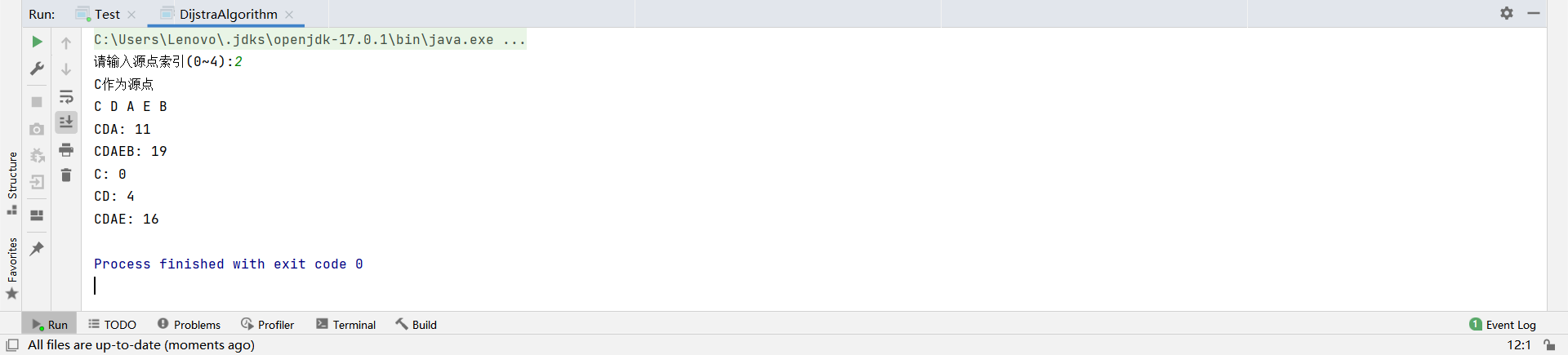
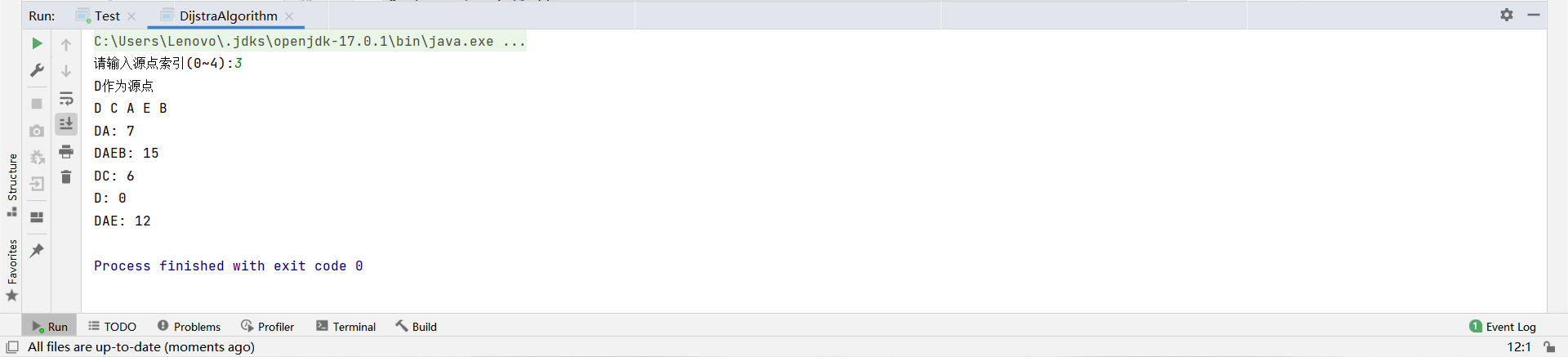
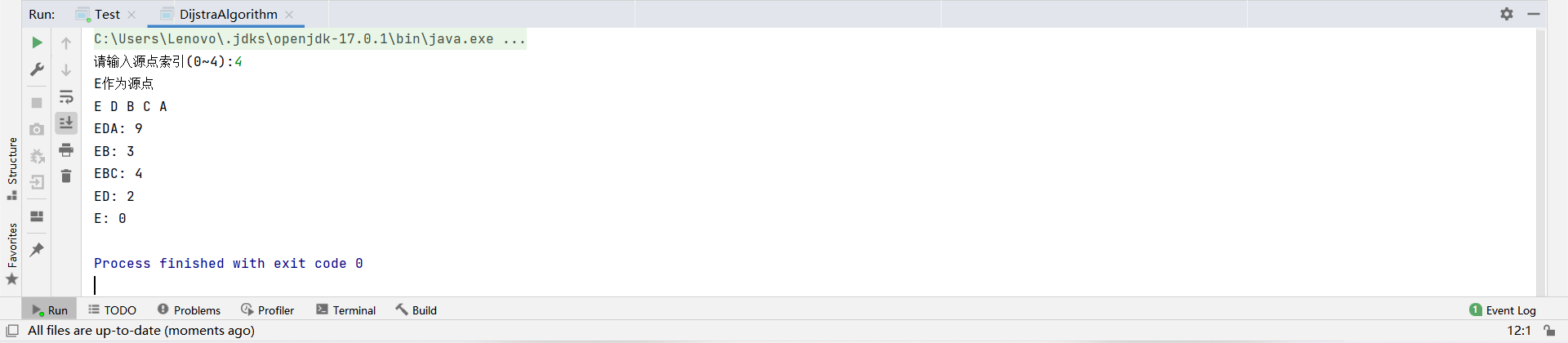
根据结果可以知道,以B为源点时路径最短。
## 3. 实验过程中遇到的问题和解决过程
- 问题1:我最开始是采用了邻接矩阵,但我一直没做出来,我的邻接矩阵一直是非常诡异的(图没了),就总有一部分对不上号。
- 问题1解决方案:最后我选择了邻接表,感觉顺畅多了。
- 问题2:在使用树的构造中,一开始和邻接矩阵的表示方法混了,把原本的-1写成了0.
- 问题2解决方案:最后改回来了,不然就会产生0默认为最小权值,输出错的值。
- 问题3:实现深度优先遍历算法时,输出的序列与实际的序列是相反的。
- 问题3解决方案:栈“先进后出”的特点,出栈的顺序与真正的遍历顺序是相反的,使用一个数组,在每一次结点入栈时记录这个结点,最后做一次倒序输出即可。
- 问题4:我问题还挺多的来着,做了好几天忘的差不多了,挺烦人的还,就这样愉快地结束吧。
## 其他
感悟:我滴🐎,好难啊。这是我做过最难的实验了,泪目了家人们。这个图的算法又多又难的,我哭了,太致命了,我感觉我啥也不会,我真的可以考试吗?这个图真的感觉写一个程序的功夫我自己人脑就出来了,太难了,还好这是最后一次了,我以后再也不想写图了,好想哭,这也是我最后一次实验报告了,谢谢老师同学们的照顾,在之后的生活中我也会继续努力学习,数据结构教会了我许多,比如教我做人,让我知道自己真的啥也不是,谢谢这么好的小公主一直很认真的教我们,临别之际,祝福各位新年快乐,平安顺遂!!!
## 参考资料
- 《Java程序设计教程(第九版)》
- 《Java软件结构与数据结构(第四版)》
- 网页搜索资料:图的遍历:https://blog.csdn.net/qq_22238021/article/details/78286798
- 网页搜索资料:https://blog.csdn.net/weixin_30384217/article/details/99115000
- 网页搜索资料:Prim算法或Kruscal算法:https://www.cnblogs.com/yghjava/p/6858364.html
- 网页搜索资料:Dijkstra算法之 Java详解:https://www.cnblogs.com/he-px/p/6677063.html

 浙公网安备 33010602011771号
浙公网安备 33010602011771号