快速排序

实现原理

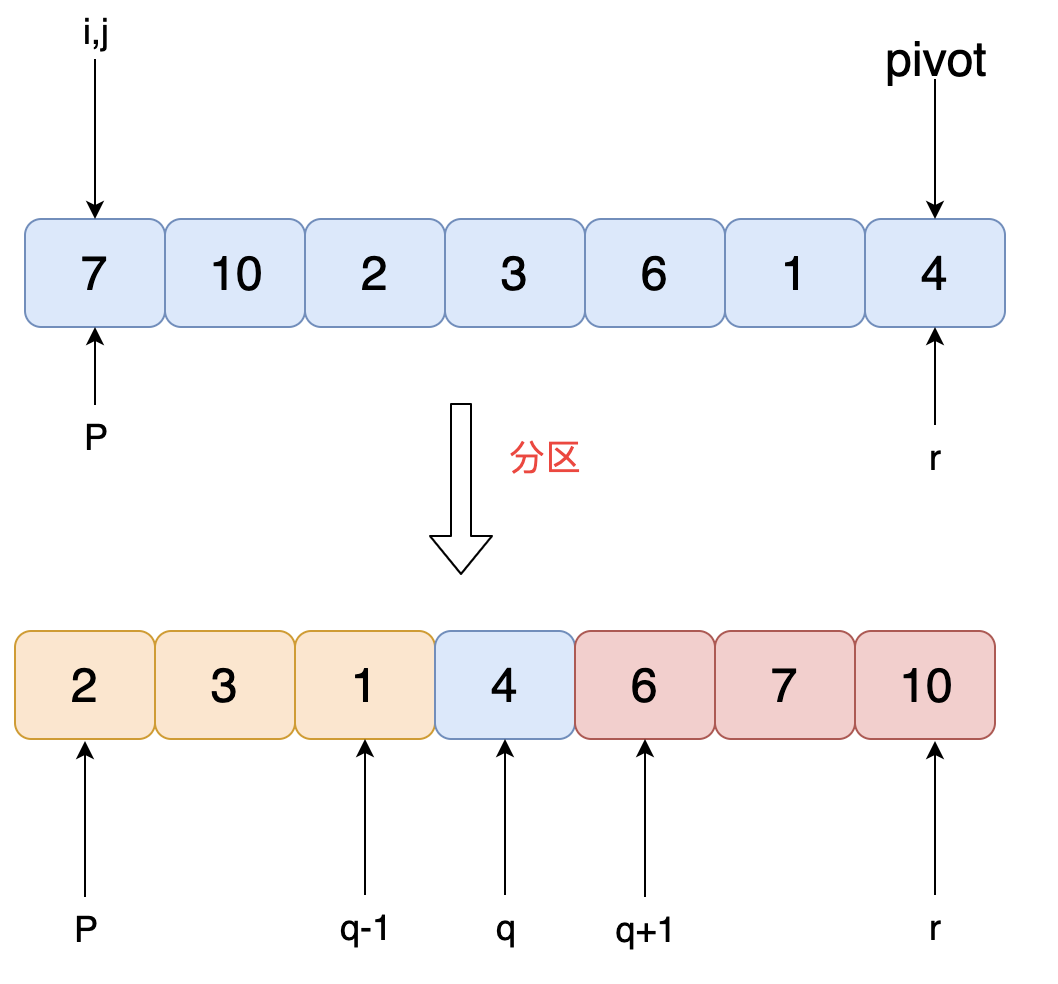
快速排序思想：如果要排数组p到r之间的一组数据，选择p到r之间任意一个一个数据作为pivot（分区点，这里选择的是s[r]作为pivot）。遍历p到r之间的数据，将小于pivot的数据放在左边，其他的放右边。经过这一步骤后数据p到r被分成了三份，前面p～q-1的数据小于pivot，q+1~r的数据大于pivot。接着递归分治实现剩下子分区的排序。

如下图所示是一次分区的结果，以数组的最后一个节点4作为pivot:

 

 

代码实现(golang)

 1 package main
 2 
 3 import "fmt"
 4 
 5 func quicklySort(s []int) []int {
 6     quickylySortImpl(s, 0, len(s)-1)
 7     return s
 8 }
 9 
10 func quickylySortImpl(s []int, p, r int) {
11     if p >= r {
12         return
13     }
14     q := partition(s, p, r)
15     quickylySortImpl(s, p, q-1)
16     quickylySortImpl(s, q+1, r)
17 }
18 
19 func partition(s []int, p, r int) int {
20     pivot := s[r]
21     i := p
22     for j := p; j <= r; j++ {
23         if s[j] < pivot {
24             s[i], s[j] = s[j], s[i]
25             i = i + 1
26         }
27     }
28     s[i], s[r] = s[r], s[i]
29     return i
30 }
31 
32 func main() {
33     fmt.Println(quicklySort([]int{7, 10, 2, 3, 6, 1, 4}))
34 }

 

程序运行输出 1，2，3，4，6，7，10

时间复杂度O(nlogn), 空间复杂度O(1)

扩展应用

O(n)时间复杂度求数组的第K大数据

 1 package main
 2 
 3 import "fmt"
 4 
 5 func findKthLargest(nums []int, k int) int {
 6     q := findKthLargestImpl(nums, 0, len(nums)-1, k)
 7     return nums[q]
 8 }
 9 
10 func findKthLargestImpl(nums []int, p, r, k int) int {
11     if p >= r {
12         return p
13     }
14     q := partition(nums, p, r)
15     fmt.Println("pq=", q)
16     if (q + 1) == k {
17         fmt.Println("q=", q)
18         return q
19     } else if (q + 1) < k {
20         q = findKthLargestImpl(nums, q+1, r, k)
21     } else {
22         q = findKthLargestImpl(nums, p, q-1, k)
23     }
24     return q
25 }
26 
27 func partition(s []int, p, r int) int {
28     pivot := s[r]
29     i := p
30     for j := p; j <= r; j++ {
31         if s[j] > pivot {
32             s[i], s[j] = s[j], s[i]
33             i = i + 1
34         }
35     }
36     s[i], s[r] = s[r], s[i]
37     return i
38 }
39 func main() {
40     fmt.Println(findKthLargest([]int{3, 2, 1, 5, 6, 4}, 2))
41 }

程序运行输出 5

需要特别注意的是程序32行由大于号变成了小于号，即把比pivot大的数据放左边，让数据从大到小，从而符合第K大的判断要求。如果求第K小则不用动。

第一遍运行数组的排序是 5， 6，4，3，2，1  q = 2即元素4，进入了代码第24行的逻辑 findKthLargestImpl(nums, 0, 1, 2)

第二遍运行数组的排序是 6，5，4，3，2，1  q = 0即元素6，进入了代码第20行的逻辑 findKthLargestImpl(nums, 1, 1, 2)

第三遍运行直接返回1,即元素5

 

posted @ 2019-06-11 16:10  我是码客  阅读(610)  评论(0)  编辑  收藏  举报