SVM 支持向量机

支持向量机就是使用了核函数的软间隔线性分类法，SVM可用于分类、回归和异常值检测（聚类）任务。“机”在机器学习领域通常是指算法,支持向量是指能够影响决策的变量。
示意图如下（绿线为分类平面，红色和蓝色的点为支持向量）：

SVM

SVM原理

由逻辑回归引入^[1]

二分类

逻辑回归是从特征中学习出一个二分类模型。分类y=1的概率$p(y=1|x;\theta)$形式化表示为$h_θ (x) = g(θ^T x)={1\over 1+e^{-θ^T x}}$ .当$θ^T x$ ≫ 0时,$h_θ (x)$=1,反之≪0时$h_θ (x)$=0.

中间的分割线即决策边界$θ^T x=0$，点到决策线的距离反映了分类正确的置信度。对于图中的C点，离分割线较近，分割线稍有变动就可能被误分类。逻辑回归便是找一条中间线使得所有点整体上离这条线最远。但实际上那些离得较远的点不需要过多考虑，而应该着重考虑靠近中线的那些点。SVM相当于将视角从全局拉到了局部。分类器表达式重写为（θ用w,b替换，函数关系有所变化）：

\[h_{ w,b} (x) = g(w ^T x + b) \\ g(z)=\begin{cases} 1 && z\ge0 \\ -1 && z\lt 0 \end{cases} \tag 1 \]

函数间隔与几何间隔（Functional and geometric margins）

给定一个训练样本$(x ^{(i)} , y ^{(i)} )$,定义函数间隔如下:

\[\hat \gamma^{(i)} = y^{(i)} (w ^T x^{(i)} + b) \tag 2 \]

其中$y^{(i)}$的值为{-1,1}，$|w ^T x + b|$越大，分类置信度越大，函数间隔越大。
其意义在于：$|w ^T x + b|$能够表示点x到超平面的距离，通过观察$|w ^T x + b|$的符号与真实类别y的符号是否一致可判断分类是否正确。同号时结果为正数。
全部样本上的函数间隔定义为：$$\hat \gamma=\min_{i=1,\dots,m}\hat \gamma^{(i)}$$
但这样定义的函数间隔存在问题，将w与b的值同时放大一定的倍数时，函数间隔也会增大。

设点A代表一个样本$(x ^{(i)},1)$，则该点在决策面$w ^T x + b = 0$上的投影点B的特征为$x ^{(i)} − γ ^{(i)} · w/||w||$，$\gamma$为样本x到分类间隔的距离. 向量$ w/||w||$为法向量。因为点B在决策面上，因此

\[\begin{align} w^T(x ^{(i)} −& γ ^{(i)} {w\over \|w\|})+b=0 \\ &↓ \\ γ ^{(i)}&=({w\over \|w\|})^Tx ^{(i)}+{b\over \|w\|} \end{align} \tag 3 \]

几何间隔可进一步表示为（令 γ 乘以对应的类别得到绝对值，当然误分类的情况就是负数了）

\[γ ^{(i)}=y^{(i)}\big(({w\over \|w\|})^Tx ^{(i)}+{b\over \|w\|}\big) \tag 4 \]

可以看出几何间隔就是函数间隔除以$\|w\|$，解决了函数间隔会随w的增大而改变的问题。当$\|w\|=1$时,几何间隔便是函数间隔;函数间隔归一化后就是几何间隔.同函数间隔一样全部样本上的几何间隔定义为所有训练样本中最小的几何间隔$$\gamma=\min_{i=1,\dots,m}\gamma^{(i)}$$.

最优间隔分类器

寻找最优间隔分类器即找出最大的几何间隔（不用函数间隔是因为缩放w使得函数间隔可无限增大）,可以形式化的表示为:

\[\begin{align} \max_{ γ,w,b} &\ \ γ \\ s.t. &\ \ y ^{(i)} (w ^T x^{(i)} + b) ≥ γ, i = 1, . . . , m \\ &\ \ \|w\| = 1 \end{align} \tag 5 \]

这里用 $\|w\|=1$ 规约 $w$,使得$y(w ^T x + b)$是几何间隔。然而 $\|w\|=1$ 不是凸函数,普通的优化求解器无法求解.考虑几何间隔和函数间隔的关系,$γ={\hat γ\over \|w\|}$,我们改写一下上面的式子:

\[\begin{align} \max_{ γ,w,b} &\ \ {\hat γ\over \|w\|} & \text{(几何间隔)} \\ s.t. &\ \ y ^{(i)} (w ^T x^{(i)} + b) ≥\hat γ, i = 1,\dots, m & \text{(函数间隔)} \end{align} \tag 6 \]

式子中仍然包含凸函数,考虑到同时将w和b扩大或缩放一定倍数,对分类结果没有影响,因此可以使得$\hat γ=1$.因此max ${\hat γ\over \|w\|}={1\over \|w\|}$等价于min $\|w\|$,等价于min ${1\over 2} \|w\|^2$,后者便于求导后的式子表达.改写之后变为二次规划问题:

\[\begin{align} \min_{ γ,w,b} &\ \ {1\over 2}\|w\|^2 \\ s.t. &\ \ y ^{(i)} (w ^T x^{(i)} + b) ≥ 1, i = 1,\dots, m \end{align} \tag 7 \]

在将函数间隔$\hat γ$设置为1时,几何间隔$γ$为$1\over \|w\|$,那么分类超平面两边的支持向量所在平面间的距离为$2\over \|w\|$. 我们可以从另外的角度来计算这个距离:

设正类和负类的两个点分别是$x^+,x^-$, 那么两条支持向量平面间距为这两点构成的向量在超平面法向量$\vec w$上的投影,间距为:

\[d=|(x^+ - x^-)\cdot {w\over \|w\|}| \]

由约束条件$y ^{(i)} (w ^T x^{(i)} + b) = 1$,得到

\[\begin{cases} w^Tx^+ + b=1 \\ w^Tx^- + b=-1 \end{cases} \]

因此 $d={|1-b-(-1-b)|\over\|w\|}={2\over \|w\|}$.

对偶问题

构造拉格朗日函数:

\[\mathcal L(w, b, α) ={1\over 2}\|w\|^2 −\sum^m_{i=1} α_ i[ y ^{(i) }(w^ T x^{(i) }+ b) − 1] \tag 8 \]

在约束条件（$\forall i, y ^{(i)} (w ^T x^{(i)} + b) ≥ 1$）都满足的情况下,且约束$α_ i\ge 0(i=1,\cdots, n)$，则优化的目标$\min_{w,b} {1\over 2}\|w\|^2$等价于$\min_{w,b}\max_{α_ i\ge 0} \mathcal L(w, b, α)$.
由于这个目标函数中先求解max的问题时涉及两个参数w和b,不太好做.而对于一般的优化问题,如果有最优解,则必定满足KKT条件,同时对于凸优化问题,如果满足KKT条件必然有最优解.^[2]我们可以将满足KKT条件的问题转换成对偶问题:$\max_{α_ i\ge 0}\min_{w,b} \mathcal L(w, b, α)$.
接下来求解对偶问题.

令$\nabla_w\mathcal L(w, b, α) =0$,求得

\[w=\sum^m_{i=1}α_ i y ^{(i) }x^{(i) } \tag{9} \]

对b求偏导得

\[\nabla_b\mathcal L(w, b, α) =-\sum^m_{i=1}α_ i y ^{(i) }=0 \tag{10} \]

将 w 和 b 代入 L 得

\[\begin{align} \mathcal L(w, b, α) =&{1\over 2}\|w\|^2 −\sum^m_{i=1} α_ i[ y ^{(i) }(w^ T x^{(i) }+ b) − 1] \\ =&{1\over 2}\sum^m_{i=1}α_ i y ^{(i)}(x^{(i)})^T\sum^m_{j=1}α_j y ^{(j) }x^{(j) } \\ & -\sum^m_{i=1}α_i y ^{(i)}(x^{(i)})^T\sum^m_{j=1}α_j y ^{(j) }x^{(j) } \\ & - b\sum^m_{i=1}α_i y ^{(i)}+\sum^m_{i=1}α_i \\ =& \sum^m_{i=1}α_i - {1\over 2}\sum^m_{i=1}\sum^m_{j=1}y ^{(i)}y ^{(j)}α_i α_j ⟨x^{(i)},x^{(j)}⟩ \end{align} \]

合并(8)(9)(10)可得原问题的对偶问题:

\[\begin{align} \max_{α} &\ \ W(α)=\sum^m_{i=1}α_ i-{1\over 2}\sum^m_{i,j=1}y ^{(i)} y ^{(j)}α_ iα_ j⟨x^{(i)},x^{(j)}⟩ \\ s.t. &\ \ α_ i ≥0, i = 1,\dots, m \\ &\ \ \sum^m_{i=1}α_ i y ^{(i) }=0 \end{align} \tag{11} \]

此时的目标函数仅与 $α$ 有关, 当求解出了各个$α_ i$的值,根据公式(9)可进而求出w, $$w=\sum^m_{i=1}α_ixy^{(i)}$$ 设超平面两边的支持向量分别为$x^+$和$x^-$,那么有:

\[\begin{cases} w^Tx^+ + b=1 \\ w^Tx^- + b=-1 \end{cases} \]

因此$b=-{1\over 2}(w^Tx^+ + w^Tx^-)$, 即:

\[b=-(\max_{i:y^{(i)}=-1}w^Tx^{(i)}+\min_{i:y^{(i)}=1}w^Tx^{(i)})/2 \]

实际上这里可以用一种叫序列最小优化算法（Sequential minimal optimization, SMO）^[3] 的快速学习算法来求解这个对偶问题.SMO目前被广泛使用于SVM的训练过程中，并在通行的SVM库LIBSVM中得到实现。^[4]
这个算法在下文介绍, 此时先不用考虑。

分类超平面与决策函数

训练完成之后就可以使用分类超平面 $w^T x + b=0$ 来对新样本进行分类了,
决策函数为$f(x)=\rm{sgn}(w^T x + b)$

此时的SVM仅能处理线性的数据,对$w^T x + b$的形式稍作变化可以引入核函数来推广到非线性分类问题:

\[w^T x + b =\sum^m_{i=1}α_ i y ^{(i) }⟨x^{(i)},x⟩+b\tag{12} \]

所有的非支持向量的$α=0$,因此内积操作只需计算少量的支持向量.

核函数

用于将数据映射到高维,从而更好得拟合模型并且还可以解决线性不可分的情况。核技巧的基本思想是通过非线性变换将输入空间(欧式空间或离散集合)对应到特征空间(希尔伯特空间),使得在输入空间的超曲面模型对应于特征空间中的超平面模型, 这样可以在特征空间中求解线性支持向量机。利用核函数升维后不一定线性可分，但是投射到的维度越高，变为线性的可能性就越大。通过核函数在低维空间中计算避免了直接在高维空间中的复杂计算。示意图如下:^[5]

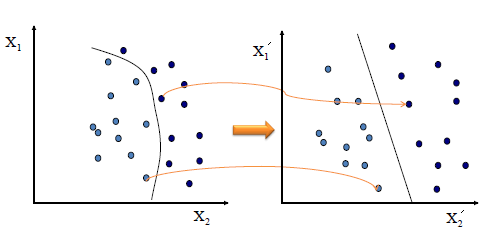
高维线性可分

举例,y与x的关系可能是3次多项式关系,因此需要将特征x扩展到三维$(x, x ^2 , x ^3)$,然后寻找特征和结果之间的模型.

我们需要将SVM公式$w^T x + b$ 中的内积从$< x ^{(i)} , z >$,映射到$< φ(x ^{(i)} ), φ(z) >$.定义映射后的内积为核函数$K(x,z)= φ(x )^T φ(z) $.

然而如果直接计算高维数据的内积,显然计算量级比原始数据的内积高.如果核函数仍然是计算低维数据,则可以不增加计算量.
核技巧举例：设$\mathbf x_1=(x_1,y_1),\mathbf x_2=(x_2,y_2)$为二维空间中的两个点,利用映射$(x,y)\mapsto (x^2,y^2,\sqrt 2xy)$将其映射到一个三维特征空间中的点$\mathbf x_1',\mathbf x_2'$.内积$\langle \mathbf x_1',\mathbf x_2'\rangle=x_1^2x_2^2+y_1^2y_2^2+2x_1y_1x_2y_2=(x_1x_2+y_1y_2)^2=(\langle\mathbf x_1,\mathbf x_2\rangle)^2$
可见,只要将这两点的原始空间中的内积取平方,无需构造新的特征向量(高维特征)便可得到新空间中对应的内积.直接根据原始空间中的向量来计算新特征空间中内积的函数称为核函数.在这个例子中核函数为$\kappa(\mathbf x_1,\mathbf x_2)=(\langle\mathbf x_1,\mathbf x_2\rangle)^2$.
对核函数的选择,现在还缺乏指导原则,实验观察结果表明,某些问题用某些核函数效果很好,用另一些就很差,但是一般来讲,径向基核函数是不会出太大偏差的一种首选方法.采用核方法，能够很方便地产生非线性分类边界。核函数要满足Mercer's定理，常见的核函数有以下几种。

linear，线性核，会产生线性分类边界。一般来说它的计算效率最高，而且需要数据最少。(相当于没有核)
poly ，多项式核，$K(x, z) = (x^T z+c)^ d$,会产生多项式分类边界,映射后特征维度为${n+d\choose d}$。
rbf，是根据与每一个支持向量的距离来决定分类边界的。$K(x, z) = \exp\big(-{\|x-z\|^2\over 2\sigma^2}\big)$,类似于高斯分布,因此称为高斯核函数,也叫做径向基函数(Radial Basis Function 简称 RBF),它能够把原始特征映射到无穷维。它是最灵活的方法，但是也需要最多的数据。比较相似的还有sigmoid 核函数等等。高斯核很灵活，而且对于训练数据效果是最好的。但是要担心过拟合。高斯核函数可以看做是对x与z的相似度的衡量.
laplace，$K(x,z)=\exp\big(-{\|x-z\|\over \sigma}\big)$
sigmoid: $K(x,z)=\tanh(ax^T z-b)$
组合: 上述核函数的线性组合或乘积.

对新样本进行分类时将式(12)中的内积用核函数计算即可.

核函数有效性判定: K 是有效的核函数等价于核函数矩阵 K 是对称半正定的。

svm核函数的选择:^[6]
如果数据比较简单,是线性可分的,那么自然是不用核函数(参数设置为线性核函数), 并且使用非线性核函数速度会变慢,且容易过拟合. 通常要按照情况选择:

如果特征维数较高(远超样本个数),那么选择线性核.
如果特征少,样本很多. 需要添加更多特征并继续使用线性核.
如果特征少(10^0 - 10^{3),样本量适中(10}1 - 10^4), 使用非线性核.

非线性核通常使用高斯核, 高斯核可以映射到无穷维,解释:
指数项 $e^{x}$ 可以通过泰勒展开映射到无穷多项

\[e^{x} \approx 1 + x + \frac{x^{2}}{2!} + \frac{x^{3}}{3!} + ... + \frac{x^{n}}{n!} \]

相应的高斯核也是指数形式：

\[\kappa \left( x_{1} , x_{2} \right) = e^{\left(- \frac{\left||x_{1} - x_{2} \right|| ^{2} }{2\sigma ^{2} } \right) } \\ = 1 + \left(- \frac{\left||x_{1} - x_{2} \right|| ^{2} }{2\sigma ^{2} } \right) + \frac{(-\frac{\left||x_{1} - x_{2} \right|| ^{2} }{2\sigma ^{2} })^{2} }{2!} + ... + \frac{(-\frac{\left||x_{1} - x_{2} \right|| ^{2} }{2\sigma ^{2} })^{3} }{3!} + ... + \frac{(-\frac{\left||x_{1} - x_{2} \right|| ^{2} }{2\sigma ^{2} })^{n} }{n!} \]

将泰勒展开式带入高斯核，我们得到了一个无穷维度的映射。

核函数推广: 核函数不仅仅用在 SVM 上, 只要在一个模型算法中出现了 $\langle x, z \rangle$ 内积形式, 我们都可以尝试使用核函数 $K(x, z)$ 去替换, 这可能会改善我们的算法。这在后文核方法/核技巧中作介绍。

正则化与非线性可分

在将数据映射到高维后可能仍然不是线性可分的, 即使是线性可分的,超平面也易受离群点的影响,难以确定这个超平面是否是我们想要的.

这时候我们应该允许一些点游离并且在模型中违背限制条件(原先的函数间隔大于 1)。对式(7)进行改变,在限制条件中加入软间隔,目标函数中加入软间隔的L1正则项作为惩罚项,得到新的模型如下:

\[\begin{align} \min_{ γ,w,b} &\quad {1\over 2}\|w\|^2+C\sum_{i=1}^m\xi_i \\ s.t. &\quad y ^{(i)} (w ^T x^{(i)} + b) ≥ 1-\xi_i, \\ &\quad \xi_i\ge 0,\quad i = 1,\dots, m \end{align} \tag {13} \]

目标函数控制了离群点的数目和程度,使大部分样本点仍然遵守限制条件。

用拉格朗日函数转化为无约束问题:

\[L(w,b,\xi,\alpha,\mu) = \frac{1}{2}||w||_2^2 +C\sum\limits_{i=1}^{m}\xi_i - \sum\limits_{i=1}^{m}\alpha_i[y_i(w^Tx_i + b) - (1 - \xi_i)] - \sum\limits_{i=1}^{m}\mu_i\xi_i \]

其中,$\mu_i \geq 0, \alpha_i \geq 0$均为拉格朗日系数。令 ${\partial L\over \partial w}={\partial L\over \partial b}={\partial L\over \partial \mu}=0$, 解得:

\[\begin{align} w=\sum^m_{i=1}α_ i y ^{(i) }x^{(i)} \\ \sum^m_{i=1}α_ i y ^{(i) }=0 \\ C−α_i−μ_i=0 \end{align} \]

代入 $L(w,b,\xi,\alpha,\mu)$, 得:

\[\begin{align} \max_{α} &\ \ W(α)=\sum^m_{i=1}α_ i-{1\over 2}\sum^m_{i,j=1}y ^{(i)} y ^{(j)}α_ iα_ j⟨x^{(i)},x^{(j)}⟩ \\ s.t. &\ \; 0 \leq \alpha_i \leq C, i = 1,\dots, m \\ &\ \ \sum^m_{i=1}α_ i y ^{(i) }=0 \end{align} \tag{14} \]

通过求解器或SMO求出$\alpha$, 进而得到w. 这个求解过程与不带软间隔的差别仅仅是$0 \leq \alpha_i$ 变为 $0 \leq \alpha_i \leq C$. 此时只剩对 b 的求解.
由于软间隔的引入,造成支持向量的增加. 原本b仅由两个支持向量确定: $b=-(\max_{i:y^{(i)}=-1}w^Tx^{(i)}+\min_{i:y^{(i)}=1}w^Tx^{(i)})/2$.
现在需要找出满足$0<α_s<C$的所有S个支持向量$(x_s,y_s)$. 支持向量满足$y_s(\sum\limits_{i=1}^{S}\alpha_iy_ix_i^Tx_s+b) = 1$, 两边同乘以$y_s$, 得$b_s^{*} = y_s - \sum\limits_{i=1}^{S}\alpha_iy_ix_i^Tx_s$, 计算所有的$b^∗_s$对应的平均值即为最终的 $b^{*} = \frac{1}{S}\sum\limits_{i=1}^{S}b_s^{*}$.^[7]

KKT

对软间隔支持向量机, KKT 条件要求:

\[\begin{cases} \alpha_i\ge 0, \mu_i\ge 0 & \text{(拉格朗日乘子大于0)} \\ y_i(w x_i+b)\ge 1-\xi_i & \text{(函数间隔)} \\ \alpha_i[y_i(w x_i+b)-1+\xi_i]=0 & \text{(拉格朗日乘数项)} \\ \xi_i\ge 0, \mu_i\xi_i=0& \text{(软间隔与乘数项)} \end{cases} \]

损失函数 hinge loss

上式soft margin SVM的目标优化问题中的 $\xi_i$ 可以理解为 loss，问题等价于

\[\min_{w,b}{1\over 2}\|w\|^2+C\sum_i\mathcal l[y_i(w^Tx_i+b)] \]

其中$\mathcal l(\cdot)$是损失函数, 常见的是 hinge loss, $\mathcal l(z)=\max(0,1-z)$. 将上式除以C,得到形式为

\[\min \mathcal L = \min_{w,b}\sum_i\mathcal l[y_i(w^Tx_i+b)]+{1\over 2C}\|w\|^2 \]

此目标函数可以看作是加 L2 regularization 的 hinge loss.

对于软间隔SVM，margin <=1 的都是支持向量.

SVM 参数: C 与 gamma

$\sigma$是高斯分布的幅宽，$\sigma$越小，高斯分布约窄高，只对支持向量附近样本有作用，对未知样本分类效果差，因此越容易过拟合；$\sigma$越大，平滑效应越大。而核系数$\gamma={1\over 2\sigma^2}$.

C 是软间隔的权重，默认值为1。如果C值很大，松弛变量$ξ_i$会很小，允许的误差也就很小，将会得到一个小间距的超平面，可能出现过拟合现象。如果数据难以区分，可以减小C值来增大软间隔。

C较大时，可能会过拟合（Low bias, high variance）；
C较小时，可能会欠拟合（High bias, low variance）；
σ较大时，可能会欠拟合（High bias, low variance）；
σ较小时，可能会过拟合（Low bias, high variance）；

SMO 优化算法与坐标上升

上文提到, 我们的软间隔分类器的优化目标是(公式14):

即在受约束的情况下求解

\[\max_αW(α_1,α_2,...,α_m) \]

我们容易联想到坐标下降(min)与坐标上升(max)方法, 使用坐标上升方法求解的思路是:

\[\begin{align} \text{Loop until} & \text{ convergence:} \\ \text{For } & {i = 1,...,m: } \\ & α_i:= \arg \max_{\hat α_i}W(α_1,...,α_{i−1}, \hat α_i,α_{i+1},...,α_m). \end{align} \]

这样,每次更新时沿着某一个分量进行更新,而不是选择总体的最优方向. 但是由于约束条件 $\sum^m_{i=1}α_ i y ^{(i) }=0$ 的存在, 当其它分量固定时 $\alpha_i=-\sum^m_{j\ne i}α_j y ^{(j)}$ 的值也是确定的, 使得这个分量无法更新.
既然无法只更新一个参数, 那更新两个即可. 这正是SMO算法的思想来源:

重复下面过程直到收敛(满足KKT条件){
（1）选择一对拉格朗日乘子 $α_ i$ 和 $α_ j$；由于组合方式有 m(m-1)/2 种, 大数据之下通常需要加速收敛. 选择的方式可以是: 选择最有可能需要优化（也就是违反KKT条件最严重）的$α_ i$，第二个变量 $α_ j$的选择标准是让|E1−E2|有足够大的变化。(E表示预测输出与期望值的差: $E_i = g(x_i)-y_i = \sum\limits_{j=1}^{m}\alpha_j y_jK(x_i, x_j)+ b - y_i$) 。^[3:1]
（2）固定其他拉格朗日乘子，只对 $α_ i$ 和 $α_ j$ 优化 ;
（3）根据优化后的 $α_ i$ 和 $α_ j$ ，更新截距 b 的值
}

支持向量

在通过优化算法求解对偶问题之后得到与每个训练样本对应的 $α_i$, 而 $α$ 向量比较稀疏, 其中的非零值所对应的训练样本即支持向量.^[8] 因此可以说 SVM 的训练过程是一个寻找支持向量及其权重 $α$ 的过程, 决策边界函数可由支持向量与 $α$ 计算得到. 寻找支持向量需要遍历一遍所有样本, 所以计算量与支持向量的个数无关. 而测试阶段是支持向量与未知样本参与运算, 测试计算量与支持向量的个数有关.

SVM + 梯度下降

SVM 是否可用 SGD?

linear SVM 原始问题(损失函数+L2正则项) 可以很容易使用SGD^[9].
通常将SVM的原问题转为对偶问题后使用核方法, SMO求解该对偶问题速度相比SGD更快.
但是原始问题也可以不经过对偶问题而使用核方法. 方式与逻辑回归/线性回归等广义线性模型一样, 设 $\mathbf w = \phi(\mathbf x)\cdot \mathbf u,\; \mathbf K = \phi(\mathbf x)^t\phi(\mathbf x)$,
对原问题加核方法得到:

\[\begin{align} \min_{w,b}J(\mathbf{w}, b) &= {1\over 2}\|w\|^2+C\sum_i\ell[y_i(w^Tx_i+b)] \\ J(\mathbf{u}, b) &= C {\displaystyle \sum\limits_{i=1}^{m} } \ell[y_i(\mathbf u^T\mathbf{K}^{(i)}+b)] + \dfrac{1}{2} \mathbf{u}^t \cdot \mathbf{K} \cdot \mathbf{u} \\ & = C {\displaystyle \sum\limits_{i=1}^{m} \max\left(0, 1 - y^{(i)} (\mathbf{u}^t \cdot \mathbf{K}^{(i)} + b)\right)} + \dfrac{1}{2} \mathbf{u}^t \cdot \mathbf{K} \cdot \mathbf{u} \end{align} \]

这样我们便可以对(u,b)进行SGD梯度下降做优化了.^[10]^[11]

那么使用SGD与SMO孰优孰劣?

SMO是EM算法/坐标上升的思想, 不一定得到全局最优解. 速度更快些.
SGD 也容易陷入局部最优, 相比SMO可能更稳定, 速度慢.
为什么感觉都是在用SMO呢? 也许是历史原因吧. 用SVM的人是不是越来越少了? 不清楚.

LR是否可用类似SMO的优化方式? 即能否使用坐标上升/下降.
答案是可以的, 但不一定效果好. 对于一个函数的求解,如果梯度计算很复杂, 那么适合用坐标上升/下降. 如果梯度计算简单,那么适合梯度下降.^[12]

多分类

可以使用两种方式将二分类扩展到多分类(n类)：

一对一(one-over-one)的方式,在任意两类样本之间设计一个SVM,因此n个类别的样本就需要设计n(n-1)/2个模型.当对一个未知样本进行分类时,最后得票最多的类别即为该未知样本的类别.
一对多(one-vs-the-rest)将训练 n 个模型，与一对一结果相近，但运行时间较短。对于未知样本,若仅一个模型输出为正类,则输出该类别,否则选择置信度最大的正类对应的类别。虽然一对一的方式训练的模型更多(存储开销和测试时间开销更大)，但是每一个模型的训练都只用了2个类别的数据,而一对多方式需要用到全部训练样例，因此当类别数很多的时候一对一开销通常更小(只要训练复杂度高于O(N)即可得到此结果)。而测试时的速度性能取决于具体的数据分布,多数情况下两者差不多.^[13]
使用多类hinge loss, 由于复杂度较高,因此很少采用.
DAGSVM（Platt et al., 2000）。对于 K 个类别，DAGSVM共有 K(K−1)/2 个分类器。每次对新的测试点分类时，只需要 K−1 对分类器进行计算。选定的分类器是根据遍历图的路径确定的。
DAG的结点(分类器)从上到下依次为1,2,3,…,k-1个。构造如下的二叉树判别结构:^[14]
```
             (第1类 vs 第k类)
         (2类 vs k类) (1类 vs k-1类)
```
(3类 vs k 类) (2类 vs k-1类) (1类 vs k-2类) (2类 vs -1类)

分类时，可以先分1类和k类，如果分类器回答属于k类就往左判断2类和k类，否则向右，依次类推。这样的话，每次向下走一步都排除掉一类，最后留下的类别即为所属类别。沿着二叉树从根走到叶子节点共比较k-1次.
优点：分类速度快，没有分类重叠现象或者分类不可分现象。
缺点：分类错误累积(前面分类器分类错误，后面分类器无法纠正)，从上到下节点的选取技巧(参照置信度)。

回归与聚类^[15]^[16]

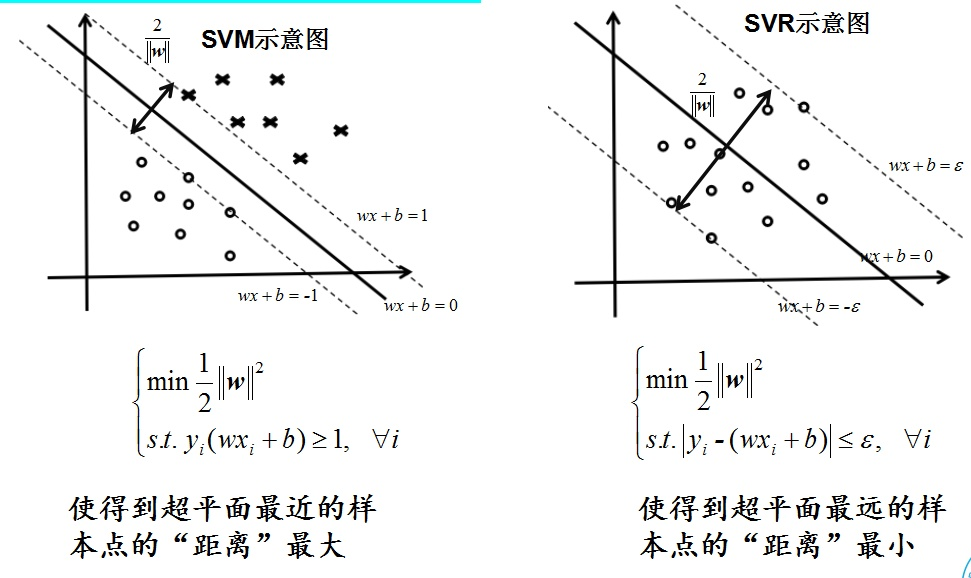
SVR（回归）与SVC（分类）的区别是使用远离预测中心的值。分类是找一个平面，使得平面边界上的点到平面的距离最远，回归是让每个点到回归线的距离最小。
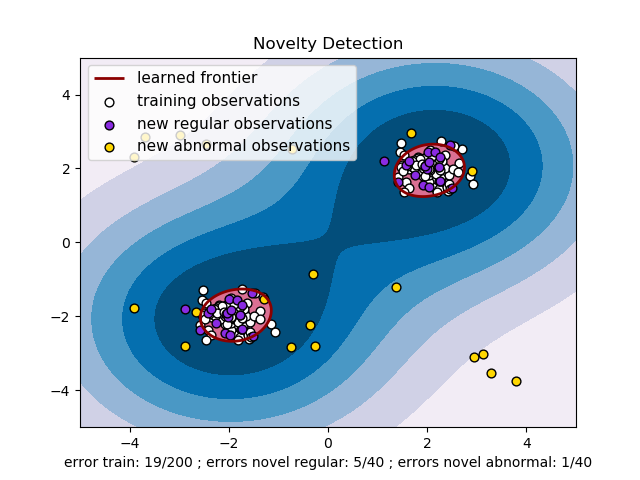
单类的SVM（OneClassSVM）可用于密度估计，特殊点检测（novelty detection），给一个样本集合，得到一个软边界使得新的样本可被判断出是否属于这个集合。属于无监督学习。
SVR示意图
Novelty and Outlier Detection

核方法

分类/回归模型的优化目标的通用形式^[17]

\[\min_\mathbf w L(X^T\mathbf w,\mathbf y)+\lambda\|\mathbf w\|^2 \]

其中 X 是 m x n 的数据矩阵, y是标签, w 是参数, L是损失函数, λ ≥ 0 是正则化参数, 这里采用L2正则项,目的是为了能够使用核函数(而L1不能够使用, 这算是L2相比于L1的一个优势吧).

最优解 w 可以由 X 空间线性变换得到: $\mathbf w =\mathbf X\mathbf v$, 这里用到了表示定理(Representer Theorem)
我们的优化目标转换为:

\[\min_\mathbf w L(X^T\mathbf w,\mathbf y)+\lambda\|\mathbf w\|^2 \\ = \min_\mathbf v L(X^T\mathbf X\mathbf v,\mathbf y)+\lambda\|\mathbf v^T\mathbf X^T\mathbf X\mathbf v\|^2 \\ = \min_\mathbf v L(K\mathbf v,\mathbf y)+\lambda\mathbf v^T K\mathbf v \]

即可运用kernel matrix: $K = X^TX$, $(K_{ij} = x^ T_i x_j)$ 进行求解. 最终的模型相当于关于 v 的线性模型了，核函数K 就相当于特征转换.

核技巧可以运用到线性回归(采用均方差损失); 逻辑回归(采用logistic loss); SVM (采用Hinge loss) 及 SVR 等模型之中.

概率值校准(calibration)

SVC 得到的输出值并非概率, 其相对值相当于分类间隔, 输出值分布不均匀, 而是集中在两侧,类似sigmoid概率密度分布曲线. 因此不能直接归一化输出值当作概率值.

有两个流行的calibration methods: Platt’s scaling(sigmoid,有参数) 与 Isotonic regression(保序回归,阶梯式函数,无参).

Platt’s scaling

在训练SVM分类器之后将SVM分类的输出值与真实类别标签作为数据训练一个额外的逻辑回归模型.^[18]
设分类器的输出为 f(x), 使用带参数的逻辑回归得到概率值:

\[{\mathrm {P}}(y=1|x)={\frac {1}{1+\exp(Af(x)+B)}} \]

式子中参数A,B均是标量, 可以通过极大似然估计进行参数估计.
另外, 由于几乎很少出现0,1这种理想的结果(以随机森林为例, 很难让所有决策树都预测正确), 该方法的提出者 Platt 建议将标签$y\in \{-1,+1\}$ 替换为$\{t_-,t_+\}$. 其中 $t_+>0.5,\ t_-<0.5$

\[\begin{align} t_{{+}} &={\frac {N_{{+}}+1}{N_{{+}}+2}} , (y = +1) \\ t_{{-}} &={\frac {1}{N_{{-}}+2}} , (y = -1) \end{align} \]

Isotonic regression

与Platt’s scaling区别在于拟合函数不同, isotonic regression 拟合的是分段非递减常量函数(piecewise-constant non-decreasing function), 即阶梯式上升的形状. 保序回归求解的如下的二次规划问题:

\[\min \sum_i w_i(y_i-\hat y_i)^2 \\ s.t. \hat y_{min}=\hat y_1\le \hat y_2\le\cdots\le\hat y_n=\hat y_{max} \]

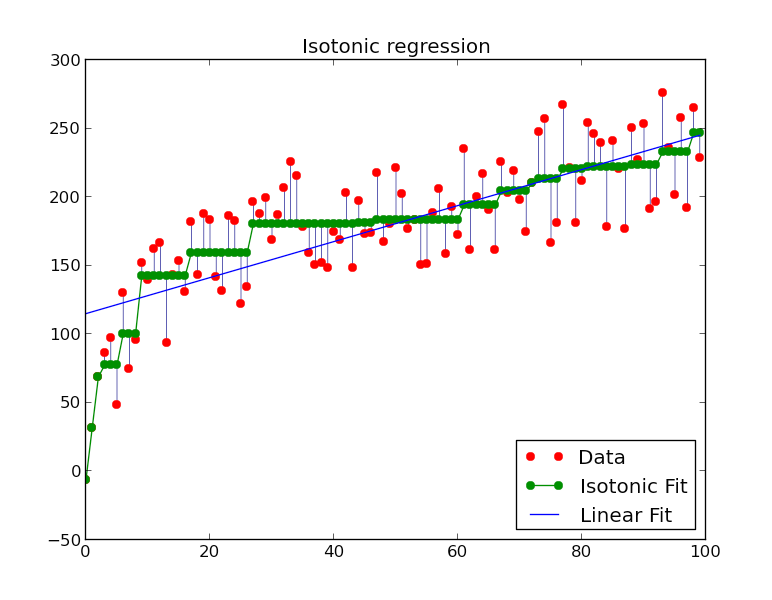
isotonic regression

Isotonic Regression的一种求解算法是pair-adjacent violators algorithm（简称PAV算法），时间复杂度是O(N)，主要思想是通过不断合并、调整违反单调性的局部区间，使得最终得到的区间满足单调性。
保序回归法：从该序列的首元素往后观察，一旦出现乱序现象停止该轮观察，从该乱序元素开始逐个吸收元素组成一个序列，直到该序列所有元素的平均值小于或等于下一个待吸收的元素。

举例：^[19]
原始序列：<9, 14, 10>
结果序列：<9, 12, 12>

原始序列：<14, 9, 10, 15>
结果序列：<11, 11, 11, 15>

保序回归可用于 CTR 预估模型的校准上.

在SVC上运用Platt’s scaling 与 isotonic regression 的结果相当. 见下图:

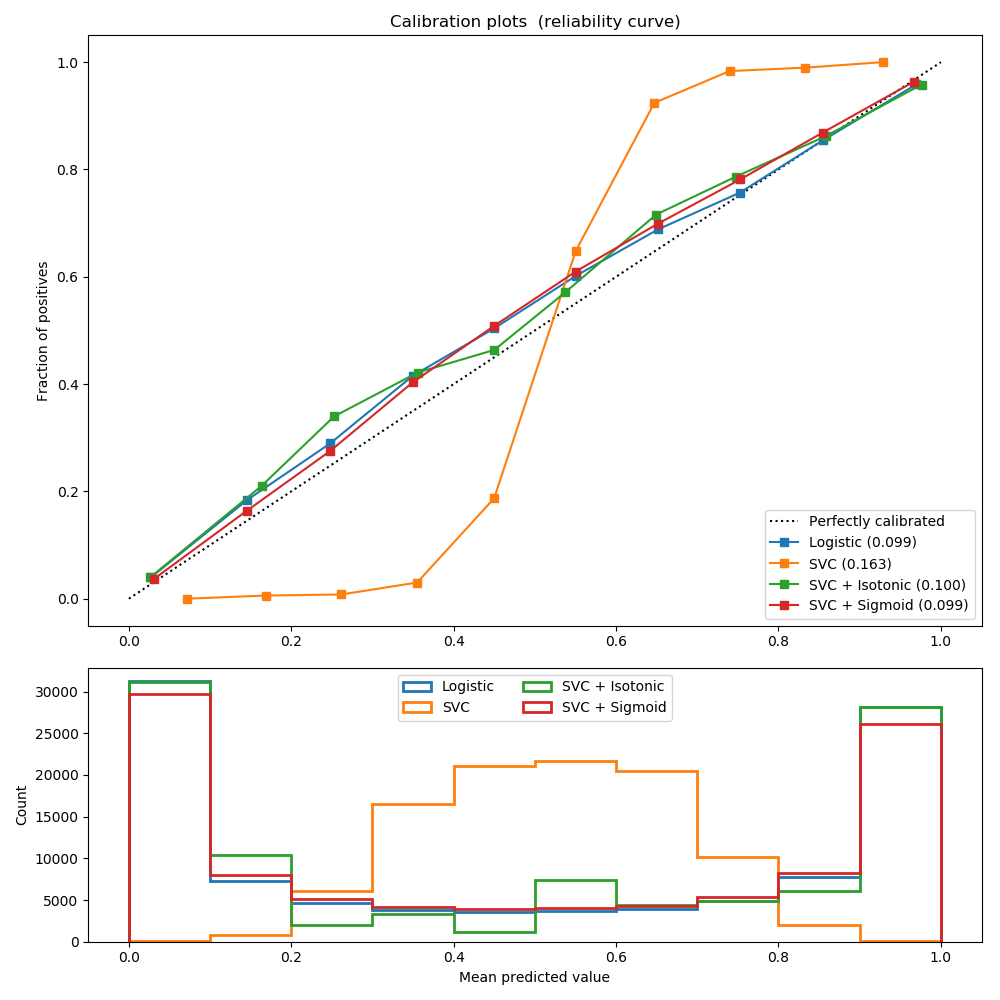
svc-calibration

而对于高斯朴素贝叶斯来说, isotonic regression 的结果很好, 而 Platt’s scaling 表现很一般, 因为朴素贝叶斯的输出的分布并非sigmoid曲线的形式.

校准方法选择

对于两种方法的选择也很简单: 如果模型是像SVM或者boosted trees(随机森林等)这种使得样本预测值的分布曲线是sigmoid形状的,而是sigmoid的一种转置形式,那么可以使用Platt’s scaling. 否则使用isotonic regression,因为它可以拟合任意形状. 在有足够多的数据的情况下, 通常isotonic regression表现地更好一些.

对于多分类的情况, 使用one-vs-rest方式对每一个类别进行calibration.^[20]

SVM 优缺点

优点：

在高维空间有效
在维度高于样本数量时也有效，在样本量少的情况下，比神经网络的效果好。
节省内存：在决策函数中仅使用部分样本（支持向量）
可以指定多种核函数

缺点：

如果特征数远比样本数多，需要精心挑选核函数和正则约束项来减轻过拟合。
SVM并不能得到概率值（需要接逻辑回归，再使用5-折交叉验证得到，比较耗时，且这种方法得到的概率值与score可能不一致，即argmax的结果可能不同）
SVM 对异常点比较敏感^[21], 异常点容易影响决策边界. 对于SVM来说, 异常点出现在中间间隔以内才会对决策边界有影响, 但是一旦受影响,影响程度会很大. 虽然有软间隔,但还是有很大可能受影响.
而对LR来说 , 所有样本共同决定拟合的结果, 每个样本点都会影响决策, 但是少量的异常点不会使全局发生太大变化.

SVM vs Softmax

score
SVM 和 softmax 均能完成多类别的分类任务,但其分类输出的打分值意义不同。其中 SVM 输出的数值大小仅仅表示所属类别的概率排序结果,该数字的绝对值大小没有物理意义。而 softmax 分类器的打分值被正则化到[0,1]之间,可以看作是各类别的概率。但是这里的概率值受参数W的正则项系数λ的影响, λ越大则权重W越接近于0,那么softmax之后各个类别的结果数值更不易区分. 因此同SVM一样,score的相对大小顺序更有意义,而绝对值意义不大.
优化方式
SVM 的处理样本时是只考虑支持向量去学习分类器, 并且当样本的分类结果中正确类别比其它类别超出margin的时候loss为0, svm不再加以优化; 而 softmax 通过非线性映射的方式减小了远离分类平面的样本点的权重,相对提升了近分类样本点的权重,二者本质思路上是一致的。

SVM 和 softmax 并没有孰优孰劣的区分,但 SVM 将原问题转化为对偶问题后只需要计算支持向量的样本点。对于复杂的问题,利用核函数能够极大的简化模型,减少计算量。^[22]

SVM vs 逻辑回归

SVM 模型可以看作逻辑回归加L2正则项, 并使用了不同的损失函数. 预测结果的概率值可以通过 Platt's scaling 得到.

线性核SVM通常和线性逻辑回归效果相当.SVM的最大化间隔的方式在某些情形下可能会比线性回归/逻辑回归模型要好一点点.

SVR vs 线性回归

优化方式不同, SVR将原始问题转换为对偶问题的求解. 损失函数不同.
SVR可使用核函数增加非线性, 原始线性回归不可以(当然也可以加入核函数).

线性SVR与LinearRegression孰优孰略, 并没有特别明确的说法. 有人更喜欢LinearRegression的可解释性.

与神经网络的结合

在训练阶段训练 VGG、AlexNet 等模型时在最后层采用 softmax 分类器。
测试时将网络模型的最后的特征作为样本单独训练一个 SVM 分类器。
对未知样本进行分类预测时先经过网络提取特征再将特征经过SVM分类。
目前主流的模型中也没有没有明确的指出 SVM 和 softmax 分类器的绝对优势。因此在不追求绝对精度的情况下,二者均可以作为模型的分类器使用。

SVM的时间复杂度^[23]

对于线性SVM,在训练时需要通过求解二次问题(quadratic problem)得到w与b,在测试时与特征数量线性相关.对于具有核函数的SVM,训练时需要选择支持向量,测试时与支持向量的个数线性相关,也与特征数量线性相关.求解二次问题涉及求矩阵的逆,时间复杂度为$O(n^3)$,而通常不需要求得最优解,只需要迭代求解得到泛化能力较好的解,因此时间复杂度可认为是$O(n^2)$.具体的线性SVM时间复杂度$O(\text{n_sample * n_features})$, RBF核函数并使用SMO求解器的SVM时间复杂度$O(\text{n_samples^2 * n_features})$.

参考

Machine Learning Course，CS229 ↩︎
支持向量机通俗导论（理解SVM的三层境界） https://blog.csdn.net/v_july_v/article/details/7624837 ↩︎
Platt, John, Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines, 1998 ↩︎ ↩︎
https://zh.wikipedia.org/wiki/序列最小优化算法 ↩︎
http://www.saedsayad.com/support_vector_machine.htm ↩︎
https://stackoverflow.com/questions/20566869/where-is-it-best-to-use-svm-with-linear-kernel ↩︎
线性支持向量机的软间隔最大化模型 https://www.cnblogs.com/pinard/p/6100722.html ↩︎
https://www.quora.com/Does-anyone-have-an-idea-on-how-to-find-support-vectors-in-1-hard-Margin-linear-SVM-2-Soft-Margin-Linear-SVM-and-3-Non-Linear-SVM ↩︎
http://www.vlfeat.org/api/svm-sgd.html ↩︎
https://stats.stackexchange.com/questions/46457/kernel-svm-in-primal-training-with-stochastic-gradient-descent ↩︎
https://stats.stackexchange.com/questions/215524/is-gradient-descent-possible-for-kernelized-svms-if-so-why-do-people-use-quadr ↩︎
https://stats.stackexchange.com/questions/146317/coordinate-vs-gradient-descent ↩︎
机器学习. 周志华. 多分类学习. ↩︎
将SVM用于多类分类 http://www.lining0806.com/将svm用于多类分类/ ↩︎
http://scikit-learn.org/stable/modules/svm.html ↩︎
支持向量机svc和svr回归和分类具体的区别 https://www.zhihu.com/question/45113186/answer/236300626 ↩︎
Lecture 7: Kernels for Classification and Regression https://people.eecs.berkeley.edu/~russell/classes/cs194/f11/lectures/CS194 Fall 2011 Lecture 07.pdf ↩︎
http://fastml.com/classifier-calibration-with-platts-scaling-and-isotonic-regression/ ↩︎
保序回归举例 https://blog.csdn.net/fsz521/article/details/7706250 ↩︎
http://scikit-learn.org/stable/modules/calibration.html ↩︎
Breakdown Point of Robust Support Vector Machine https://arxiv.org/abs/1409.0934 ↩︎
svm vs softmax. http://cs231n.github.io/linear-classify/#svmvssoftmax ↩︎
SVM的时间复杂度 ↩︎

posted @ 2017-07-02 21:00 康行天下阅读(3278) 评论(8) 编辑收藏举报

刷新页面返回顶部

明也无涯

不积跬步无以至千里

SVM 支持向量机

SVM原理

由逻辑回归引入^[1]

函数间隔与几何间隔（Functional and geometric margins）

最优间隔分类器

对偶问题

分类超平面与决策函数

核函数

正则化与非线性可分

KKT

损失函数 hinge loss

SVM 参数: C 与 gamma

SMO 优化算法与坐标上升

支持向量

SVM + 梯度下降

多分类

回归与聚类^[15]^[16]

核方法

概率值校准(calibration)

Platt’s scaling

Isotonic regression

校准方法选择

SVM 优缺点

SVM vs Softmax

SVM vs 逻辑回归

SVR vs 线性回归

与神经网络的结合

SVM的时间复杂度^[23]

参考

公告

明也无涯

不积跬步无以至千里

SVM 支持向量机

SVM原理

由逻辑回归引入[1]

函数间隔与几何间隔（Functional and geometric margins）

最优间隔分类器

对偶问题

分类超平面与决策函数

核函数

正则化与非线性可分

KKT

损失函数 hinge loss

SVM 参数: C 与 gamma

SMO 优化算法 与 坐标上升

支持向量

SVM + 梯度下降

多分类

回归与聚类[15][16]

核方法

概率值校准(calibration)

Platt’s scaling

Isotonic regression

校准方法选择

SVM 优缺点

SVM vs Softmax

SVM vs 逻辑回归

SVR vs 线性回归

与神经网络的结合

SVM的时间复杂度[23]

参考

公告

由逻辑回归引入^[1]

SMO 优化算法与坐标上升

回归与聚类^[15]^[16]

SVM的时间复杂度^[23]