深度学习网络层之 Pooling
pooling 是仿照人的视觉系统进行降维(降采样),用更高层的抽象表示图像特征,这一部分内容从Hubel&wiesel视觉神经研究到Fukushima提出,再到LeCun的LeNet5首次采用并使用BP进行求解,是一条线上的内容,原始推动力其实就是仿生,仿照真正的神经网络构建人工网络。
至于pooling为什么可以这样做,是因为:我们之所以决定使用卷积后的特征是因为图像具有一种“静态性”的属性,这也就意味着在一个图像区域有用的特征极有可能在另一个区域同样适用。因此,为了描述大的图像,一个很自然的想法就是对不同位置的特征进行聚合统计。这个均值或者最大值就是一种聚合统计的方法。
做窗口滑动卷积的时候,卷积值就代表了整个窗口的特征。因为滑动的窗口间有大量重叠区域,出来的卷积值有冗余,进行最大pooling或者平均pooling就是减少冗余。减少冗余的同时,pooling也丢掉了局部位置信息,所以局部有微小形变,结果也是一样的。
pooling层通常的作用是:减少空间大小,减少网络参数,防止过拟合。
pooling 种类
最常见的池化操作为最大池化和平均池化:
最大池化 Max Pooling
前向传播:选图像区域的最大值作为该区域池化后的值。
反向传播:梯度通过最大值的位置传播,其它位置梯度为0。
平均池化 Average Pooling(也称mean pooling)
前向传播:计算图像区域的平均值作为该区域池化后的值。
反向传播:梯度取均值后分给每个位置。
对于Average Pooling的输入\(X=x_1,x_2,...x_n\),输出\(\displaystyle f(X) = \frac{1}{n} \sum_{i=1}^n x_i\)
Stochastic Pooling
论文Stochastic Pooling for Regularization of Deep Convolutional Neural Networks提出了一种简单有效的正则化CNN的方法,能够降低max pooling的过拟合现象,提高泛化能力。对于pooling层的输入,根据输入的多项式分布随机选择一个值作为输出。训练阶段和测试阶段的操作略有不同。
训练阶段
- 前向传播
(1)归一化pooling的输入,作为每个激活神经元的分布概率值\(p_i={a_i\over\sum_{k\in R_j}a_k}\).
(2)从基于\(p\)的多项式分布中随机采样一个位置的值作为输出。 - 反向传播
跟max pooling类似,梯度通过被选择的位置传播,其它位置为0.
测试阶段
如果在测试时也使用随机pooling会对预测值引入噪音,降低性能。取而代之的是使用按归一化的概率值加权平均。比使用average pooling表现要好一些。因此在平均意义上,与average pooling近似,在局部意义上,则服从max pooling的准则。
解释分析
按概率加权的方式可以被看作是一种模型平均融合的方式,在pooling区域不同选择方式对应一个新模型。训练阶段由于引入随机性,所以会改变网络的连接结构,导致产生新的模型。在测试阶段会同时使用这些模型,做加权平均。假设网络有d层pooling层,pooling核大小是n,那么可能的模型有\(n^d\)个。这比dropout增加的模型多样性要多(dropout率为0.5时相当于n=2)。
在CIFAR-10上三种pooling方法的错误率对比:
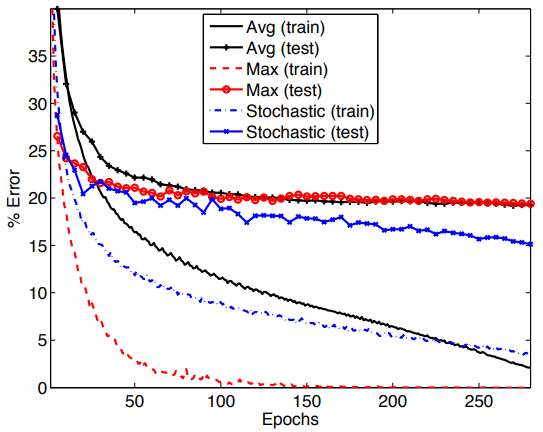
pooling 选择与实际应用
通常我们使用Max Pooling,因为使用它能学到图像的边缘和纹理结构。而Average Pooling则不能。Max Pooling通常用以减小估计值方差,在方差不太重要的地方可以随意选择Max Pooling和Average Pooling。Average Pooling用以减小估计均值的偏移。在某些情况下Average Pooling可能取得比Max Pooling稍好一些的效果。
average pooling会弱化强激活值,而max pooling保留最强的激活值却容易过拟合。
虽然从理论上说Stochastic Pooling也许能取得较好的结果,但是需要在实践中多次尝试,随意使用可能效果变差。因此并不是一个常规的选择。
按池化是否作用于图像中不重合的区域(这与卷积操作不同)分为一般池化(Gerneral Pooling)与重叠池化(OverlappingPooling)。
常见设置是filter大小F=2,步长S=2或F=3,S=2(overlapping pooling,重叠);pooling层通常不需要填充。
代码实现
caffe cpu版pooling层实现代码pooling_layer.cpp:
template <typename Dtype>
void PoolingLayer<Dtype>::Forward_cpu(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top) {
...
switch (this->layer_param_.pooling_param().pool()) {
case PoolingParameter_PoolMethod_MAX:
const int pool_index = ph * pooled_width_ + pw;
for (int h = hstart; h < hend; ++h) {
for (int w = wstart; w < wend; ++w) {
const int index = h * width_ + w;
if (bottom_data[index] > top_data[pool_index]) {
top_data[pool_index] = bottom_data[index];
if (use_top_mask) {
top_mask[pool_index] = static_cast<Dtype>(index);
} else {
mask[pool_index] = index;
}
}
}
}
case PoolingParameter_PoolMethod_AVE:
...
for (int i = 0; i < top_count; ++i) {
top_data[i] = 0;
}
for (int h = hstart; h < hend; ++h) {
for (int w = wstart; w < wend; ++w) {
top_data[ph * pooled_width_ + pw] +=
bottom_data[h * width_ + w];
}
}
top_data[ph * pooled_width_ + pw] /= pool_size;
...
case PoolingParameter_PoolMethod_STOCHASTIC:
NOT_IMPLEMENTED;
}
template <typename Dtype>
void PoolingLayer<Dtype>::Backward_cpu(const vector<Blob<Dtype>*>& top,
const vector<bool>& propagate_down, const vector<Blob<Dtype>*>& bottom) {
if (!propagate_down[0]) {
return;
}
switch (this->layer_param_.pooling_param().pool()) {
case PoolingParameter_PoolMethod_MAX:
// The main loop
if (use_top_mask) {
top_mask = top[1]->cpu_data();
} else {
mask = max_idx_.cpu_data();
}
for (int n = 0; n < top[0]->num(); ++n) {
for (int c = 0; c < channels_; ++c) {
for (int ph = 0; ph < pooled_height_; ++ph) {
for (int pw = 0; pw < pooled_width_; ++pw) {
const int index = ph * pooled_width_ + pw;
const int bottom_index =
use_top_mask ? top_mask[index] : mask[index];
bottom_diff[bottom_index] += top_diff[index];
}
}
bottom_diff += bottom[0]->offset(0, 1);
top_diff += top[0]->offset(0, 1);
if (use_top_mask) {
top_mask += top[0]->offset(0, 1);
} else {
mask += top[0]->offset(0, 1);
}
}
}
break;
case PoolingParameter_PoolMethod_AVE:
// The main loop
for (int n = 0; n < top[0]->num(); ++n) {
for (int c = 0; c < channels_; ++c) {
for (int ph = 0; ph < pooled_height_; ++ph) {
for (int pw = 0; pw < pooled_width_; ++pw) {
int hstart = ph * stride_h_ - pad_h_;
int wstart = pw * stride_w_ - pad_w_;
int hend = min(hstart + kernel_h_, height_ + pad_h_);
int wend = min(wstart + kernel_w_, width_ + pad_w_);
int pool_size = (hend - hstart) * (wend - wstart);
hstart = max(hstart, 0);
wstart = max(wstart, 0);
hend = min(hend, height_);
wend = min(wend, width_);
for (int h = hstart; h < hend; ++h) {
for (int w = wstart; w < wend; ++w) {
bottom_diff[h * width_ + w] +=
top_diff[ph * pooled_width_ + pw] / pool_size;
}
}
}
}
// offset
bottom_diff += bottom[0]->offset(0, 1);
top_diff += top[0]->offset(0, 1);
}
}
break;
case PoolingParameter_PoolMethod_STOCHASTIC:
NOT_IMPLEMENTED;
break;
...
}
Stochastic Pooling的前向传播过程示例theano代码:stochastic_pool.py
caffe中的Stochastic Pooling实现:
只为GPU做了代码实现,并需要与 CAFFE engine一块使用,需要在pooling_param 里边设置pool类型:STOCHASTIC ,在pooling_param 中设置engine: CAFFE(如果使用GPU运行,默认引擎是cuDNN).
Stochastic Pooling实现代码pooling_layer.cu:
void StoPoolForwardTrain(..,Dtype* const rand_idx,..) {
/*
rand_idx是随机选的pooling核上的位置比例,目前实现方式是使用如下的均匀分布产生函数生成:
caffe_gpu_rng_uniform(count, Dtype(0), Dtype(1),
rand_idx_.mutable_gpu_data());
*/
...
Dtype cumsum = 0.;
const Dtype* const bottom_slice =
bottom_data + (n * channels + c) * height * width;
// First pass: get sum
for (int h = hstart; h < hend; ++h) {
for (int w = wstart; w < wend; ++w) {
cumsum += bottom_slice[h * width + w];
}
}
const float thres = rand_idx[index] * cumsum;
// Second pass: get value, and set index.
cumsum = 0;
for (int h = hstart; h < hend; ++h) {
for (int w = wstart; w < wend; ++w) {
cumsum += bottom_slice[h * width + w];
if (cumsum >= thres) {// 轮盘赌,均匀分布
rand_idx[index] = ((n * channels + c) * height + h) * width + w;
top_data[index] = bottom_slice[h * width + w];
return;
}
}
}
...
}
void StoPoolForwardTest(...){
...
Dtype cumsum = 0.;
Dtype cumvalues = 0.;
const Dtype* const bottom_slice =
bottom_data + (n * channels + c) * height * width;
// First pass: get sum
for (int h = hstart; h < hend; ++h) {
for (int w = wstart; w < wend; ++w) {
cumsum += bottom_slice[h * width + w];// 求和
cumvalues += bottom_slice[h * width + w] * bottom_slice[h * width + w];// 求平方和
}
}
top_data[index] = (cumsum > 0.) ? cumvalues / cumsum : 0.;
...
}
进一步阅读
LeCun的“Learning Mid-Level Features For Recognition”对前两种pooling方法有比较详细的分析对比。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号