损失函数

监督学习中通常通过对损失函数最优化（最小化）来学习模型。
本文介绍了几种损失函数和正则化项以及正则化对模型的影响。

损失函数

损失函数度量模型一次预测的好坏，风险函数度量平均意义下模型预测的好坏。
模型的输入输出是随机变量(X,Y)遵循联合分布P(X,Y),损失函数的期望是：

\[R_{exp}(f)=E_P[L(Y,f(X))]=\int_{\mathcal X\times \mathcal Y}L(y,f(x))P(x,y)dxdy \]

这称为风险函数或期望损失。
学习的目标就是选择期望风险最小的模型，由于联合分布是未知的，所以上式无法直接计算。
对于一个有N个样本的训练数据集的平均损失称为经验风险（empirical risk）或经验损失（empirical loss）:$R_{emp}(f)={1\over N}\sum_{i=1}^NL(y_i,f(x_i))$。

根据大数定理，当样本容量N趋于无穷时，经验风险趋于期望风险，所以在现实当中使用经验风险来估计期望风险。

经验风险最小化 & 结构风险最小化

经验风险最小化：

\[\min_{f\in \mathcal F}{1\over N}\sum_{i=1}^NL(y_i,f(x_i)) \]

当样本容量足够大时具有良好的学习效果。然而当样本容量小时可能产生过拟合现象。
结构风险最小化是为了防止过拟合而提出来的策略，添加了正则化(regularization):

\[\min_{f\in \mathcal F}{1\over N}\sum_{i=1}^NL(y_i,f(x_i))+\lambda J(f) \]

其中$J(f)$是模型的复杂度.

几种损失函数

1.Softmax(cross-entropy loss)

Softmax分类器是logistic(二类)泛化到多类的情况。

Softmax函数 $f_j(z)=\frac{e^{z_j}}{\sum_k e^{z_k}}$ 将输入值转换到[0,1]区间内，可以作为类别概率值或者置信度。Softmax使得最大的$z_j$输出结果最接近1，其余接近0，另外可使负数变成非负。
Softmax函数取负对数得到cross-entropy loss。通常人们使用"softmax loss"这个词时指的就是cross-entropy loss，有时也称对数似然损失。

\[L_i=-log(\frac{e^{z_{y_i}}}{\sum_j e^{z_j}})=-z_{y_i}+log{\sum_j e^{z_j}} \]

$z_j$表示在类别j上的得分,$y_i$表示真实类别.损失值的范围为$[+\infty,1]$,在真实类别上的得分越高,损失越低.

Softmax 总体样本的损失为:

\[\mathcal L(X,Y) = -\frac{1}{N}\sum^m_{i}\sum^K_{j}1\{j=y^{(i)}\}\log(p_{i,j}) \]

其中$p_{i,j} = \frac{\exp(z_{i,j})}{\sum_j \exp(z_{i,j})}$ 表示样本 i 预测类别为 j 的概率. $z_{j}$ 是前一层的输出 $a_{j}^{L-1}$的线性组合:$z_{j}=w_ja_{j}^{L-1}+b_j$.

偏导:

\[\begin{align} {\partial L\over\partial w_{j}^L} &=-y_j(1-p_j) a_j^{L-1} \\ {\partial L\over\partial b_j^L} &=p_j^L-y_j \end{align} \]

极大似然估计视角

与极大似然估计法推导逻辑回归损失一样, 求极大似然转换为求极小负对数:

\[\begin{align} \max& \prod_i^{m} p_j^{1\{j=y^{(i)}\}} \\ \Rightarrow& \log\prod_i^m \sum_j^{K} p_j^{1\{j=y^{(i)}\}} =\sum_i^m \sum_j^{K}1\{j=y^{(i)}\}\log p_j \\ \to \min& (-\sum_i^m\sum_j^{K}1\{j=y^{(i)}\}\log p_j) \end{align} \]

信息论视角

真实分布p和估计分布q之间的cross-entropy为$H(p,q)=−∑_xp(x)\log q(x)$,Softmax分类器正是为了最小化估计的类别概率（$q=\frac{e^{s_{y_i}}}{\sum_j e^{s_j}}$）和真实值（p=[0,…1,…,0],在yi位置处是一个单独的1）的交叉熵。另外，交叉熵又可写作：$H(p,q)=H(p)+D_{KL}(p||q)$,即p的熵和KL散度（Kullback-Leibler divergence，一种距离度量方式）的和。由于H(p)=0,所以最小化损失函数即最小化KL散度，意味着使预测值更接近真实值。

caffe中的多类逻辑回归损失： MultinomialLogisticLossLayer 直接接收前一层的每类概率预测值，loss为$E=-{1\over N}\sum_{n=1}^N\log(\hat p_{n,l_n})$,其中$\hat p_{n,l_n}$表示第n个样本真实类别标签$l_n$多对应的预测值，而其它类别的值为0，乘积为0，所以公式较为简单。

如果想直接由置信度等非概率值计算损失，可以采用SoftmaxWithLossLayer ，其作用等同于先使用SoftmaxLayer映射成概率分布, 再接上 multinomial logistic loss. 唯一不同之处在于SoftmaxWithLossLayer梯度数值计算比分成两层计算更稳定.

提高数值稳定性的技巧：由于指数计算结果可能很大，对较大的数进行除法操作可能不稳定，可以采用如下转换技巧将数值减小：

\[\frac{e^{f_{y_i}}}{\sum_j e^{f_j}} = \frac{Ce^{f_{y_i}}}{C\sum_j e^{f_j}} = \frac{e^{f_{y_i} + \log C}}{\sum_j e^{f_j + \log C}} \]

常用的C值设为$\log C = -\max_j f_j$. 但是如果数据跨度比较大的话,Softmax的结果不能很好地刻画原数据中的相互大小关系, 需要控制数据的维度.

2.logistic loss

使用均方误差(Mean Squared Error, MSE)损失($L={1\over 2N}\sum_i^N (\hat y_i-y_i)^2$, 或称L2 损失)进行梯度下降训练时loss的下降曲线可能同sigmoid曲线一样先慢中间快最后又慢,原因是最后层用了sigmoid,并且求偏导会包含sigmoid的导数.那么,在不舍弃sigmoid的情况下如何增快学习?能否让loss曲线更平滑?

logistic loss函数定义:

\[\begin{eqnarray} C = -\frac{1}{n} \sum_x \left[y \ln a + (1-y ) \ln (1-a) \right] \nonumber \end{eqnarray} \]

表示n种输入情况x对应结果的平均.其中,y为期望值（只有0，1两种值）,a为输出值a=sigmoid(wx+b).

损失函数需要满足两个条件:

函数值非负
当输出值趋近于期望值时,函数值趋于0(相同时等于0就更好了)

而logistic loss函数同时满足这两个条件,因此可以作为损失函数.对于第二个条件的验证可能不太容易,让a=y时画出函数曲线可能比较直观.简单的验证方法是让所有的y设为1,则a趋于1时函数值趋于0.

下面求梯度:

\[\begin{align} {\partial C\over\partial w_j} &={1\over n}\sum_x x_j(a-y) \\ {\partial C\over\partial b} &={1\over n}\sum_x (a-y) \end{align} \]

从中可以看出学习的快慢取决于error=a-y,误差大时学得快,小时学得慢.

拓展到多层网络多输出y值的情况,L表示最后一层:

\[\begin{eqnarray} C = -\frac{1}{n} \sum_x \sum_j \left[y_j \ln a^L_j + (1-y_j) \ln (1-a^L_j) \right] \tag{多个输出y值}\end{eqnarray} \]

总结：logistic loss几乎总是比均方损失函数好;如果在输出层使用的是线性激励而不是sigmoid这样的非线性层,那么使用差方函数是可以的,不会存在由于初始参数设置不当而学习率开始比较慢的问题.

别名：logarithmic loss（log loss,二值标签通常为{-1,+1}），有时候也称为cross-entropy loss（名字有些混乱，与Softmax使用的损失函数类似，也是从cross entropy推出来的）。
换种形式表示：

\[L(w) = -\frac{1}{N} \sum_{i=1}^N \left[y_i \log \hat y_i + (1-y_i ) \log (1-\hat y_i) \right] \]

sigmoid同样涉及指数运算,需要规避溢出问题(在log的参数接近0时得到负无穷).

将$\hat y_i={1\over 1+e^{-x_i}}$代入$L(w)$,化简可得:

\[L(w)=-{1\over N}\sum_{i=1}^N[y_ix_i+\log({e^{-x_i}\over 1+ e^{-x_i}})] \]

当$x_i\ge 0$时,$L(w)$中的log项可以通过$-x_i-\log(1+e^{-x_i})$计算;
当$x_i\lt 0$时，log项可以通过$-\log(1+e^{x_i})$来计算.

L2 均方损失和交叉熵损失之间的区别:

均方损失主要做回归问题,也可以用于分类.而交叉熵损失仅用于分类.这两者的显著区别是交叉熵损失仅考虑真实类别所输出的值,而均方损失考虑每个类别. 均方损失的结果会服从高斯分布,而高斯分布正是连续变量的分布,均方损失可由高斯分布的极大似然估计的负对数得到:

\[\begin{align} p(x)&=N(\mu,\sigma)={1\over \sqrt{2\pi}\sigma}e^{(x-\mu)^2\over 2\sigma^2} \\ \max \log P(D)&=\max_p\log\prod_i^N P(D_i) \\ &=\max \sum_i^N \log P(D_i) \\ &=\max[-{N\over 2}\log(2\pi\sigma^2)-{1\over 2\sigma^2}\sum_i^N(D_i-\mu)^2] \end{align} \]

Softmax 回归 vs. k 个二元分类器

如果各个类别是互斥的，那么选择softmax回归分类器更合适。如果类别间有交叉或者是父子关系，建立多个独立的 logistic 回归分类器更加合适。

3.hinge loss (SVM)

Hinge loss 用于最大化间隔分类器中（以SVM分类器为代表）。
二分类损失函数定义为：$\ell(y) = \max(0, 1-t \cdot y)$,其中y表示分类器的输出值，t为真实类别（t = ±1），那么当t与y符号相同时，损失较小。符号相反时随y单调递增。
损失函数的形状类似“合页”(蓝色线 E(z) = max(0,1-z) )：

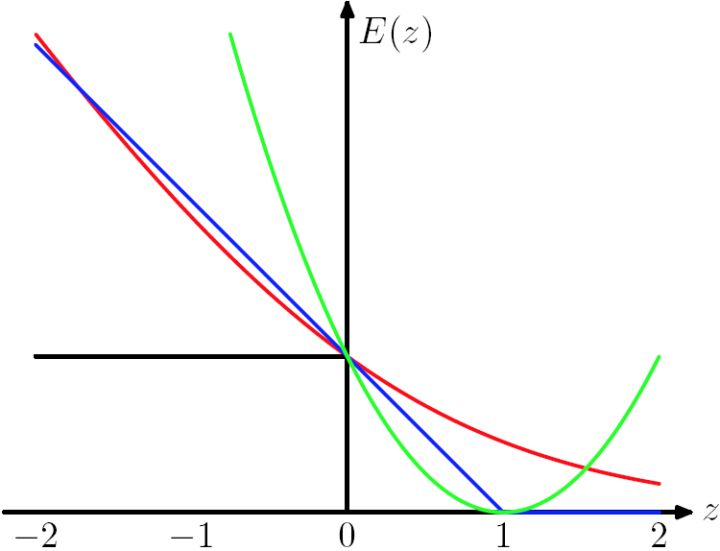
hinge-loss-curve

多分类损失函数的一种定义形式为（Weston and Watkins提出）^[1]：

\[\ell (y)=\sum_{j\neq t}\max(0,s_j-s_t+\Delta) \]

表示样本 x 上的损失,$s_j=f(x_i,W)_j$为第j类的得分,所以设计该损失的目标是使预测的其它类别的得分相比于真实类别的得分低于$\Delta$这个数量(如$\Delta$取1).其中$\Delta$是软间隔。可以看到这种损失的定义方式仅考虑不正确的预测类别。另有其它定义方式^[1:1]。

多个损失函数组合

caffe网络中可以定义多个损失层,如EUCLIDEAN_LOSS与SOFTMAX_LOSS,并设置$\lambda$为loss_weight: 100.0,那么损失函数为:

\[\mathcal L={1\over 2N}\sum_{n=1}^N\|y_n-\hat y_n\|_2^2-\lambda{1\over N}\sum_{n=1}^N\log(\hat p_{n,l_n}) \]

参数正则化

单凭最小化简单的损失函数可能会过拟合,过拟合时参数往往较多(波动大),那么可以考虑将参数加入到损失函数中去限制波动.通常通过正则化惩罚减小过拟合是很有必要的.

L1正则项

L1正则化项为$\lambda\sum|\theta_j|$ ,$\lambda$是正则化的强度。其导数是$\lambda w$,则权重更新为:W += -lambda * W,可以看出是线性递减的。L1正则化有"截断"作用，可以在特征选择中使用L1正则化有效减少特征的数量（Lasso会自动进行参数缩减和变量选择）。

原损失函数为$C_0$,则L1: $C=C_0+{\lambda\over n}\sum_w |w|$,梯度下降的更新为:

\[w\to w-{\eta\lambda\over n}\operatorname{sgn}(w)-\eta{{\partial C_0\over\partial w}} \]

符号函数在$w$大于0时为1,小于0时为-1.在$w=0$时$|w|$没有导数,因此可令sgn(0)=0,在0处不使用L1正则化.

L2正则项

L2正则化项为$\lambda\sum_{j=1}^n\theta_j^2$

加上L2损失后$C=C_0+{\lambda\over 2n}\sum_w w^2$,使得网络偏向于学习比较小的权重.

L2对偏导的影响.相比于未加之前,权重的偏导多了一项${\lambda\over n}w$,偏置的偏导没变化.那么在梯度下降时$w$的更新变为:$w\to w-\eta ({\partial C_0\over\partial w}+{\lambda\over n}w)=(1-{\eta\lambda\over n})w-\eta{{\partial C_0\over\partial w}}$,可以看出$w$的系数使得权重下降加速,因此L2正则也称weight decay(caffe中损失层的weight_decay参数与此有关).对于随机梯度下降(对一个mini-batch中的所有x的偏导求平均):

\[\begin{align} w &\to (1-{\eta\lambda\over n})w-{\eta\over m}\sum_x{{\partial C_x\over\partial w}} \\ b &\to b-{\eta\over m}\sum_x{{\partial C_x\over\partial b}} \end{align} \]

L1 vs. L2 :

L1减少的是一个常量,L2减少的是权重的固定比例
孰快熟慢取决于权重本身的大小:权重较大时可能L2快,较小时L1快.
因为1范数不可导，因此L1的没有解析解（闭式解）。

关于L1和L2正则的更详细分析，参考Lasso回归与Ridge回归 pdf

L1 相比于 L2 为什么容易获得稀疏解？

L1项在0点附近的导数为正负1, 而L2在0点附近的导数比L1的要小, 这样L1使得接近于0的参数更容易更新为0. 而L2的在0点附近的梯度远小于1时对参数更新不再起作用,因此得到的参数存在很多接近于0但不是0的情况. 其实也是一场原损失函数与正则项之间的拉锯战.^[2]

L1, ReLU怎么求导?

在0点处不可导, 多种办法解决:

次梯度法
坐标下降法
近似方法, 在0点附近的区域用可微分的近似函数替代

什么是次梯度
次梯度法能够用于不可微的目标函数。当目标函数可微时，对于无约束问题次梯度法与梯度下降法具有同样的搜索方向。
次导数：对于一元函数来讲，若在点x处的左导数＜右导数，那么在该点的次导数是一个集合：[左导数，右导数]，即大于左导数小于右导数的任意数值都可以作为该点的次导数。考虑y=|x|，在x=0处的左导数是-1，右导数是1，那么在该点的次导数就是从-1到1的所有数值组成的集合。

ReLU (= max{0, x}) 函数在0点的次导数是[0,1]; L1 norm在0点的次导数是[-1,1]. 那么我们该怎么使用次导数呢? 我们可以从区间中选择其中一个值作为0点的导数. 但是如果不同的取值会造成不同的结果, 采用次梯度法进行最优值的搜索将会非常耗时. 幸运的是在前向传播中ReLU/abs(0)的结果为0时,反向传播时梯度需要乘上前向传播的结果,梯度总是为0,所以ReLU在0点的梯度值设置成任意值均可. 因此在反向传播过程中取[0,1]中的任意值均可. 而通常我们选择0即可,比如Caffe/Tensorflow框架中的abs函数在0点的梯度通过代码计算出来是0, 梯度符合sign函数的定义. 将导数固定为0的另外一个好处是能够得到一个更稀疏的矩阵表示.

Elastic net

另一种正则化方法是Elastic net（论文），它混合了Lasso和Ridge回归，进行了权衡。Elastic net评估形式为：$$ \hat{\beta} = \underset{\beta}{\operatorname{argmin}} (| y-X \beta |^2 + \lambda_2 |\beta|^2 + \lambda_1 |\beta|_1)$$

Max-norm regularization

限制权重最大值的范数不超过常量约束c（$\Vert \vec{w} \Vert_2 < c$），其中c通常为3或4.。Max-norm regularization 之前已被用于协同过滤算法(collaborative filtering ，Srebro and Shraibman, 2005)。可以提高随机梯度下降训练的性能，可用于防止梯度爆炸。

Dropout

Dropout可以与Max-norm regularization，较大的初始学习率和较高的动量（momentum）等结合获得比单独使用Dropout更好的效果。

损失函数解决类别平衡问题

针对在模式识别问题存在的类别不平衡问题，通常我们会采用对少样本类别进行重复采样(过采样)，或是基于原样本的空间分布产生人工数据。然而有时候这两种方法都不好进行。

2015 年 ICCV 上的一篇论文《Holistically-nested edge detection》提出了名为 HED 的边缘识别模型，试着用改变损失函数的定义来解决这个问题。如对于二分类问题中的log损失：$l=-\sum_{k=0}^n[Q_k \log p_k+(1-Q_k)(1-\log p_k)]$

如样本集的标签值分别为 (1, 1, 0, 1, 1, 0, …)，则似然估计值(全部样本均预测正确的概率)为：$L=p_0\cdot p_1\cdot(1-p_2)\cdot p_3\cdot p_4\cdot(1-p_5)\cdot\dots$

HED 使用了加权的 cross entropy 函数。例如，当标签 0 对应的样本极少时，加权的损失函数定义为：$l=-\sum_{k=0}^n[Q_k \log p_k+W(1-Q_k)(1-\log p_k)]$

W需要大于 1。此时考虑似然函数：$L=p_0\cdot p_1\cdot(1-p_2)^W\cdot p_3\cdot p_4\cdot(1-p_5)^W\cdot\dots$

可见类别为 0 的样本在似然函数中重复出现了，比重因此而增加。通过这种办法，我们虽然不能实际将少样本类别的样本数目扩大，却通过修改损失函数达到了基本等价的效果。

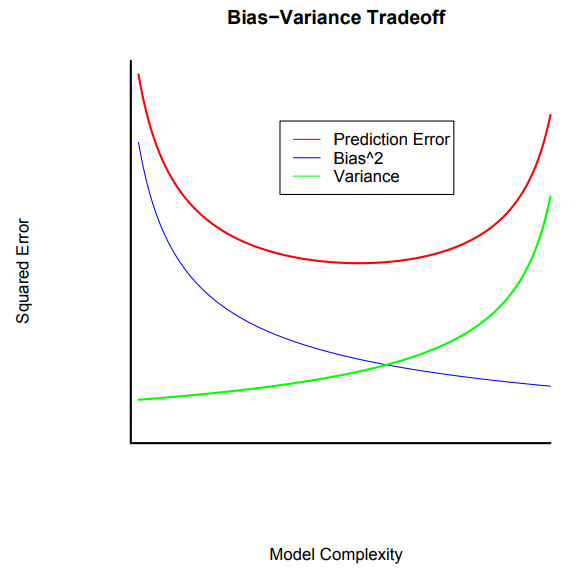
Bias−Variance Tradeoff

posted @ 2017-02-17 20:47 康行天下阅读(8104) 评论(1) 编辑收藏举报

刷新页面返回顶部

明也无涯

不积跬步无以至千里

损失函数

损失函数

经验风险最小化 & 结构风险最小化

几种损失函数

1.Softmax(cross-entropy loss)

2.logistic loss

3.hinge loss (SVM)

多个损失函数组合

参数正则化

L1正则项

L2正则项

Elastic net

Max-norm regularization

Dropout

损失函数解决类别平衡问题

Bias−Variance Tradeoff

公告