神经网络之权重初始化

权重初始化

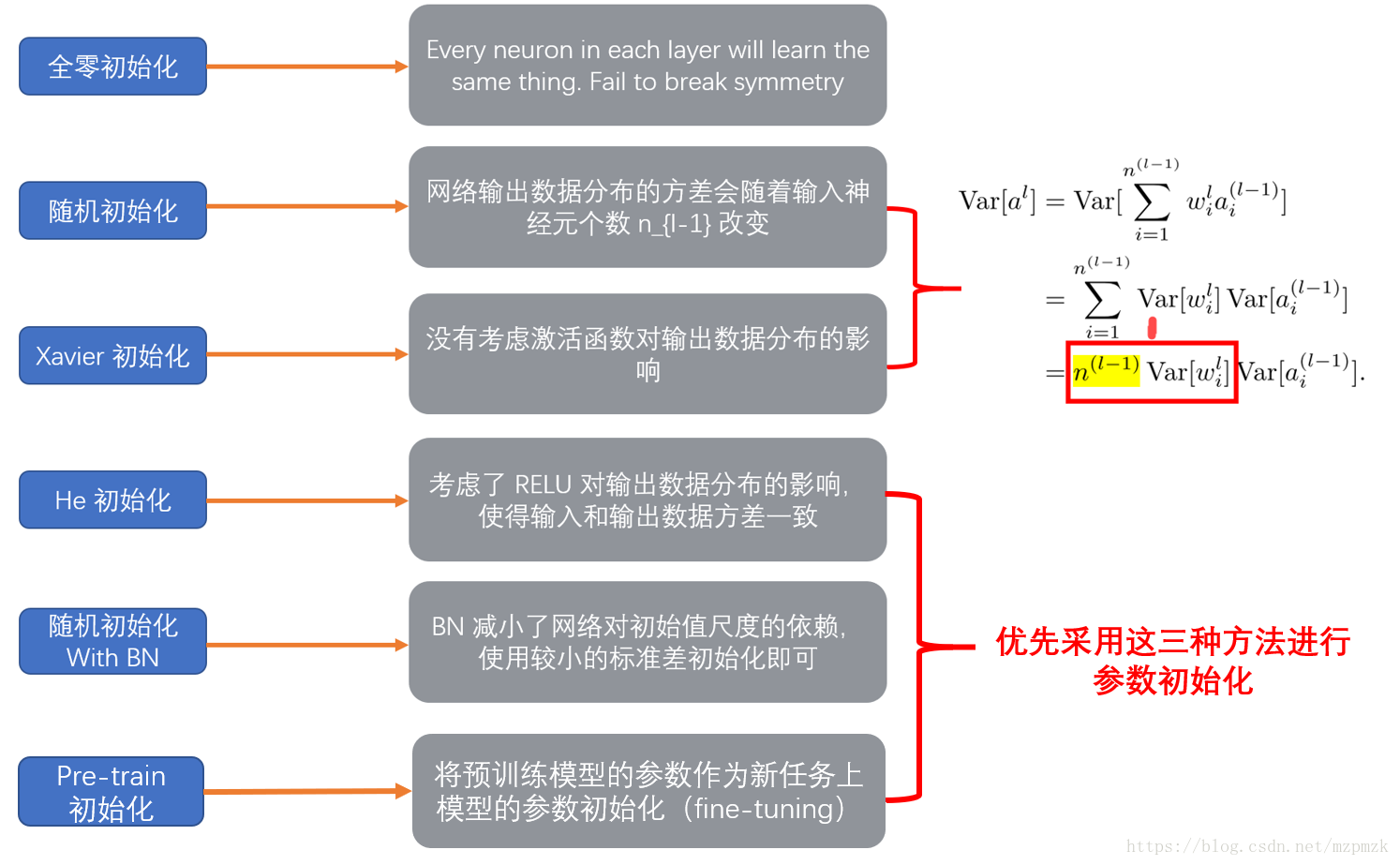
模型权重的初始化对于网络的训练很重要, 不好的初始化参数会导致梯度传播问题, 降低训练速度; 而好的初始化参数, 能够加速收敛, 并且更可能找到较优解. 如果权重一开始很小，信号到达最后也会很小；如果权重一开始很大，信号到达最后也会很大。不合适的权重初始化会使得隐藏层的输入的方差过大,从而在经过sigmoid这种非线性层时离中心较远(导数接近0),因此过早地出现梯度消失.如使用均值0,标准差为1的正态分布初始化在隐藏层的方差仍会很大. 不初始化为0的原因是若初始化为0,所有的神经元节点开始做的都是同样的计算,最终同层的每个神经元得到相同的参数.

好的初始化方法通常只是为了增快学习的速度(加速收敛),在某些网络结构中甚至能够提高准确率.

下面介绍几种权重初始化方式.

1. 初始化为小的随机数,如均值为0,方差为0.01的高斯分布:
   W=0.01 * np.random.randn(D,H) 然而只适用于小型网络,对于深层次网络,权重小导致反向传播计算中梯度也小,梯度"信号"被削弱.
2. 上面1中的分布的方差随着输入数量的增大而增大,可以通过正则化方差来提高权重收敛速率,初始权重的方式为正态分布: w = np.random.randn(n) / sqrt(n). 这会使得中间结果\(z=\sum_i w_ix_i+b\)的方差较小,神经元不会饱和,学习速度不会减慢.
   论文 Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification by He et al. 中阐述了ReLU神经元的权值初始化方式,方差为2.0/n, 高斯分布权重初始化为: w = np.random.randn(n) * sqrt(2.0/n), 这是使用ReLU的网络所推荐的一种方式.
   论文[Bengio and Glorot 2010]: Understanding the difficulty of training deep feedforward neuralnetworks 中推荐使用 \(\text{Var}(W) = \frac{2}{n_\text{in} + n_\text{out}}\).
3. Xavier (均匀分布)
4. MSRA

上述初始化方式的1,2仅考虑每层输入的方差, 而后两种方式考虑输入与输出的方差, 保持每层的输入与输出方差相等. 2,4 方法中针对ReLU激活函数, 放大了一倍的方差.

Xavier权重初始化

Xavier初始化可以帮助减少梯度弥散问题， 使得信号在神经网络中可以传递得更深。是最为常用的神经网络权重初始化方法。

算法根据输入和输出神经元的数量自动决定初始化的范围: 定义参数所在的层的输入维度为n,输出维度为m,那么参数将从\([-{\sqrt{6\over m+n}},{\sqrt{6\over m+n}}]\)均匀分布中采样。

公式推导

假设输入一层X，输出一层Y，那么

\[Y = W_1X_1 + W_2X_2 + \dotsb + W_n X_n \]

按照独立变量相乘的方差公式，可以计算出：

\[\text{Var}(W_iX_i) = E[X_i]^2 \text{Var}(W_i) + E[W_i]^2 \text{Var}(X_i) + \text{Var}(W_i)\text{Var}(X_i) \]

我们期望输入X和权重W都是零均值，因此简化为

\[\text{Var}(W_iX_i) = \text{Var}(W_i)\text{Var}(X_i) \]

进一步假设所有的\(X_i,W_i\)都是独立同分布，则有：

\[\text{Var}(Y) = \text{Var}(W_1X_1 + W_2X_2 + \dotsb + W_n X_n) = n\text{Var}(W_i)\text{Var}(X_i) \]

即输出的方差与输入有关，为使输出的方差与输入相同，意味着使\(n\text{Var}(W_i)=1\).因此\(\text{Var}(W_i) = \frac{1}{n}=\frac{1}{n_{in}}\).

如果对反向传播的梯度运用同样的步骤，可得：\(\text{Var}(W_i) = \frac{1}{n_\text{out}}\).

由于\(n_{in},n_{out}\)通常不相等，所以这两个方差无法同时满足，作为一种折中的方案，可使用介于\(\frac{1}{n_{in}},\frac{1}{n_{out}}\)之间的数来代替：简单的选择是\(\text{Var}(W_i) = \frac{2}{n_\text{in} + n_\text{out}}\).

可以根据均匀分布的方差，反推出W的均匀分布：

由于 [a,b] 区间的均匀分布的方差为：\(\text{Var}={(b-a)^2\over 12}\)，使其零均值，则b=-a,所以\(\text{Var}={(2b)^2\over 12}=\frac{2}{n_\text{in} + n_\text{out}}\)，可得\(b={\sqrt{6}\over \sqrt{n_{in}+n_{out}}}\).

因此，Xavier初始化的就是按照下面的均匀分布（uniform distribution）：

\[W \sim U[-{\sqrt{6}\over \sqrt{n_j+n_{j+1}}},{\sqrt{6}\over \sqrt{n_j+n_{j+1}}}] \]

xavier权重初始化的作用，使得信号在经过多层神经元后保持在合理的范围（不至于太小或太大）。

caffe当前的xavier实现代码：

/* 输入blob的shape：(num, a, b, c)对应(输出channel,输入channel,b*c=kernel size)
 扇入 fan_in = a * b * c
 扇出 fan_out = num * b * c
 scale = sqrt(3 / n) 这里的n根据参数决定：fan_in, fan_out, 或着平均。
 这里的sqrt(3 / n)中当n=(n_j + n_{j+1})/2时就是上面式子中的$\sqrt{6}/\sqrt{n_j + n_{j+1}}.
 然后用[-scale,scale]的均匀分布随机采样初始化权重
*/
template <typename Dtype>  
class XavierFiller : public Filler<Dtype> {  
 public:  
  explicit XavierFiller(const FillerParameter& param)  
      : Filler<Dtype>(param) {}  
  virtual void Fill(Blob<Dtype>* blob) {
    int fan_in = blob->count() / blob->num();  
    int fan_out = blob->count() / blob->channels();  
    Dtype n = fan_in;  
    if (this->filler_param_.variance_norm() == 
        FillerParameter_VarianceNorm_AVERAGE) {  
      n = (fan_in + fan_out) / Dtype(2);  
    } else if (this->filler_param_.variance_norm() ==  
        FillerParameter_VarianceNorm_FAN_OUT) {  
      n = fan_out;  
    }  
    Dtype scale = sqrt(Dtype(3) / n);
    caffe_rng_uniform<Dtype>(blob->count(), -scale, scale,  
        blob->mutable_cpu_data());
  }  
};  

MSRA Filler

上边所提的初始化方式为使每层方差一致，从而不会发生前向传播爆炸和反向传播梯度消失等问题。对于ReLU激活函数，其使一半数据变成0，初始时这一半的梯度为0，而tanh和sigmoid等的输出初始时梯度接近于1.因此使用ReLU的网络的参数方差可能会波动。论文Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification,Kaiming He中提出使用\(\text{Var}(W) = \frac{2}{n_\text{in}}\)放大一倍方差来保持方差的平稳。

前向和后向推导的方差均控制在\({2\over n}\),综合起来使用均值为0,方差为\(\sqrt{4\over n_{in}+n_{out}}\)的高斯分布.

caffe MSRA Filler实现代码：

/**
 * Fills a Blob with values $ x \sim N(0, \sigma^2) $
 * A Filler based on the paper [He, Zhang, Ren and Sun 2015]: 
 * Specifically accounts for ReLU nonlinearities.
 */
template <typename Dtype>
class MSRAFiller : public Filler<Dtype> {
 public:
  explicit MSRAFiller(const FillerParameter& param)
      : Filler<Dtype>(param) {}
  virtual void Fill(Blob<Dtype>* blob) {
    CHECK(blob->count());
    int fan_in = blob->count() / blob->num();
    int fan_out = blob->count() / blob->channels();
    Dtype n = fan_in;  // default to fan_in
    if (this->filler_param_.variance_norm() ==
        FillerParameter_VarianceNorm_AVERAGE) {
      n = (fan_in + fan_out) / Dtype(2);
    } else if (this->filler_param_.variance_norm() ==
        FillerParameter_VarianceNorm_FAN_OUT) {
      n = fan_out;
    }
    Dtype std = sqrt(Dtype(2) / n);
    caffe_rng_gaussian<Dtype>(blob->count(), Dtype(0), std,
        blob->mutable_cpu_data());
    CHECK_EQ(this->filler_param_.sparse(), -1)
         << "Sparsity not supported by this Filler.";
  }
};

bias初始化

通常初始化为0(若初始化为0.01等值,可能并不能得到好的提升,反而可能下降)

Batch Normalization

在网络中间层中使用 Batch Normalization 层一定程度上能够减缓对较好的网络参数初始化的依赖，使用方差较小的参数分布即可. 参考论文 Batch Normalization。

总结

1. 当前的主流初始化方式 Xavier,MSRA 主要是为了保持每层的输入与输出方差相等, 而参数的分布采用均匀分布或高斯分布均可.
2. 在广泛采用 Batch Normalization 的情况下, 使用普通的小方差的高斯分布即可.
3. 另外, 在迁移学习的情况下, 优先采用预训练的模型进行参数初始化.

参考

• CS231n
• https://blog.csdn.net/mzpmzk/article/details/79839047