EM 算法

期望最大化算法 (EM) 算法是通过不断求解下界的极大化逼近求解对数似然函数极大化的算法.

假设，有一个含有隐含变量 \(z\) 的模型，其概率密度函数为 \(P(x,z|θ)\)。现在，我们希望得到模型的参数估计 \(\theta\):

\[\begin{align} \hat{\theta} &=\mathop{\arg \max}_{\theta}\ell (x|\theta) \\ \ell(x|\theta) & = \log \prod_i p(x^{(i)}|\theta) \\ & = \mathop{\sum}_{i}\log p(x^{(i)}|\theta) \\ & = \mathop{\sum}_{i}\log\mathop{\sum}_{z^{(i)}}p(x^{(i)},z^{(i)}|\theta) \\ & = \mathop{\sum}_{i}\log\mathop{\sum}_{z^{(i)}}Q_i(z^{(i)})\frac{p(x^{(i)},z^{(i)}|\theta)}{Q_i(z^{(i)})} \end{align} \]

其中让 Q 函数表示样例关于隐含随机变量 z 的某种分布， Q 满足的条件

\[Q_i(z^{(i)})\ge0,\mathop{\sum}_{z^{(i)}}Q_i(z^{(i)})=1 \]

如果 z 是连续性的，那么 Q 是概率密度函数，需要将求和符号换做积分符号。

当 Q 函数时概率密度函数时, 上式中的 log 项看作是期望

\[\log \mathbb E(\frac{p(x^{(i)},z^{(i)}|\theta)}{Q_i(z^{(i)})})\ge \mathbb E(\log\frac{p(x^{(i)},z^{(i)}|\theta)}{Q_i(z^{(i)})}) \]

这里应用了Jensen不等式, 取大于等于号是因为log函数是个上凸的函数.
此时的对数似然函数为:

\[\ell(x|\theta) = \mathop{\sum}_{i}\log\mathop{\sum}_{z^{(i)}}Q_i(z^{(i)})\frac{p(x^{(i)},z^{(i)}|\theta)}{Q_i(z^{(i)})} \\ \ge \sum_i \sum_{z^{(i)}}Q_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)}|\theta)}{Q_i(z^{(i)})} \]

我们的目标是最大化对数似然函数\(\ell(x|\theta)\), 通过不等式转换成了求下界,因此我们希望不等式右侧的值越大越好.
式子中的 Q 函数尚且没有定义, 接下来通过Jensen不等式的等号成立条件得到 Q 的数学表达式.
令Jensen不等式中的等号成立,即

\[\frac{p(x^{(i)},z^{(i)}|\theta)}{Q_i(z^{(i)})}=c \iff p(x^{(i)},z^{(i)}|\theta)=cQ_i(z^{(i)}) \\ \iff Q_i(z^{(i)})=\frac {p(x^{(i)},z^{(i)}|\theta)}{c} \]

其中c是个常量,并且有\(\mathop{\sum}_{z^{(i)}}Q_i(z^{(i)})=1\)

\(\sum_z p(x^{(i)},z^{(i)};\theta)=\sum_zcQ_i(z^{(i)})=c\)
进而可得：

\[Q_i(z^{(i)})=\frac {p(x^{(i)},z^{(i)}|\theta)}{c}=\frac{p(x^{(i)},z^{(i)}|\theta)}{\sum_z p(x^{(i)},z^{(i)}|\theta)}=\frac{p(x^{(i)},z^{(i)}|\theta)}{p(x^{(i)}|\theta)}=p(z^{(i)}|x^{(i)};θ) \]

这时,我们得到了Q函数的一种计算公式,即后验概率 \(p(z^{(i)}|x^{(i)};θ)=\frac{p(x^{(i)},z^{(i)}|\theta)}{p(x^{(i)}|\theta)}\). 在样本x和参数θ已知的情况下,p(z)是可以计算的,如果不理解怎样计算,可以参考《统计学习方法》中掷硬币的例子中的E步.
接下来通过求得的Q继续最大化极大似然估计, M步:

\[\hat \theta =\mathop{\arg \max}_{\theta} \sum_i \sum_{z^{(i)}}Q_i(z^{(i)})\log\frac{p(y_j,z^{(i)}|\theta)}{Q(z^{(i)})} \]

M 步对上式中的\(\theta\)求偏导, 此时的 \(Q_i(z^{(i)})\) 是常数.因此等价于

\[\hat \theta =\mathop{\arg \max}_{\theta} \sum_i \sum_{z^{(i)}}Q_i(z^{(i)})\log {p(y_j,z^{(i)}|\theta)} \]

在《统计学习方法》 和维基百科中将后式定义为\(Q(\theta,\theta^{(i)})\), 是对z的条件概率分布\(p(z^{(i)}|x^{(i)};θ)\)的期望. 在 E 步中求\(Q(\theta,\theta^{(t)})\), 在M步中最大化\(Q(\theta,\theta^{(t)})\).

EM算法的整体流程

EM算法按照如下思想应对含隐变量的问题：

  1. 模型建立: 设置参数\(\theta\)的初始值.
  2. E步: 求Q函数(隐变量的条件概率密度，将其他参数看作常量，猜测样本属于每个类别的概率), 是一个调整隐变量分布函数的过程.
  3. M步: 求极大似然，得到新的参数(利用E步得到的概率值去更新参数)
  4. 收敛判别
    一般情况下，找到两个较小的正数ξ1,ξ2使得两次迭代的差别为:

\[|\theta^{(t+1)}-\theta^{(t)}|<\xi_1 \\ \text{or} \\ |Q(\theta^{(t+1)},\theta^{(t)})-Q(\theta^{(t)},\theta^{(t)})|<\xi_2 \\ (\Delta\ell(\theta)<\xi_2) \]

则停止迭代，否则继续迭代E步与M步，直到收敛。

几点说明

  1. 参数的初值是可以任意选择的, 但是 EM 算法对初值是敏感的. (联想到k-means算法也是对初始值敏感的)
  2. EM 算法不能保证找到全局最优解. 但是每次迭代都会使似然函数增大, 能够达到局部极值. 后文给出证明。
    EM算法的两步都是在最大化, E步是最大化似然函数的下界(通过Jenson不等式等号成立得到最大值), M 步是最大化似然函数, 因此可以看作是一种坐标上升法.[1] 另外, EM算法思想的体现还有: k-means, smo优化.

EM算法的优化过程：

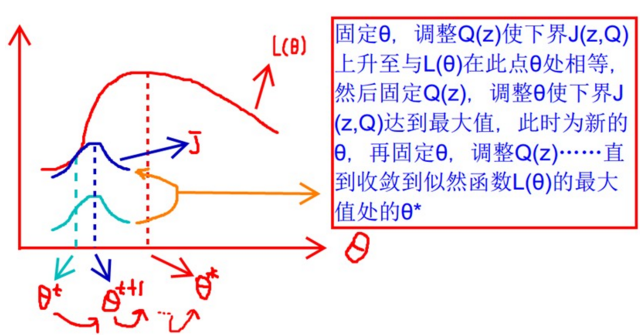
EM算法的优化过程

收敛性证明

如果在迭代过程中极大似然值稳步上升, 那么我们就能证明收敛性.
在第 t 次迭代的 E 步中使不等式中的等号成立, 即

\[\ell(\theta^{(t)})= \sum_i \sum_{z^{(i)}}Q_i^{(t)}(z^{(i)})\log\frac{p(x^{(i)},z^{(i)}|\theta^{(t)})}{Q_i^{(t)}(z^{(i)})} \]

在 M 步中 \(Q_i\) 固定, 对 \(\ell(\theta^{(t)})\) 最大化得到 \(\theta^{(t+1)}\).

\[\begin{align} \ell(\theta^{(t+1)}) &= \mathop{\sum}_{i}\log\mathop{\sum}_{z^{(i)}}Q_i^{(t)}(z^{(i)})\frac{p(x^{(i)},z^{(i)}|\theta^{(t+1)})}{Q_i^{(t)}(z^{(i)})} \\ &\ge \sum_i \sum_{z^{(i)}}Q_i^{(t)}(z^{(i)})\log\frac{p(x^{(i)},z^{(i)}|\theta^{(t+1)})}{Q_i^{(t)}(z^{(i)})} \\ &\ge \sum_i \sum_{z^{(i)}}Q_i^{(t)}(z^{(i)})\log\frac{p(x^{(i)},z^{(i)}|\theta^{(t)})}{Q_i^{(t)}(z^{(i)})} \\ &=\ell(\theta^{(t)}) \end{align} \]

算法应用

EM 算法可用于无监督学习. 如生成式模型由联合概率分布P(X,Y)表示,
X是观测数据,而Y是隐变量(未观测数据). 隐马尔可夫模型的无监督学习也是 EM 算法的一个重要应用.
高斯混合模型的参数估计是 EM 算法的一个重要应用. 高斯混合模型中的每个模型是高斯分布模型, 如果将高斯分布替换成任意的概率分布,那么称为一般混合模型.

附录 - Jensen’s inequality[2]

设 \(f(X)\) 是下凸的函数, 那么有:

\[E[f(X)] ≥ f(EX) \]

下凸函数

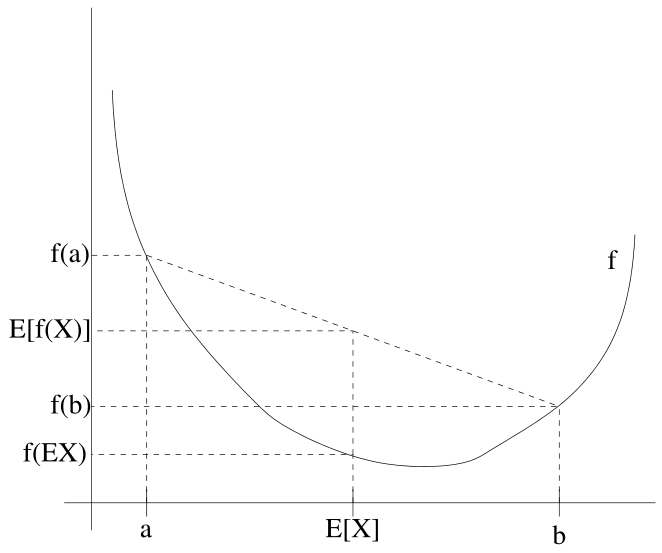
参考

  1. https://en.wikipedia.org/wiki/Expectation–maximization_algorithm ↩︎

  2. http://cs229.stanford.edu/notes/cs229-notes8.pdf ↩︎

posted @ 2018-07-19 00:03  康行天下  阅读(389)  评论(0)  编辑  收藏  举报