决策树

决策树 Decision Tree

类似于流程图,多叉树的结构,每个内部节点表示在一个属性上的测试,每个叶子节点代表类或类分布.其基本思想是以信息熵为度量构造一棵熵值下降最快的树,到叶子节点处的熵值为0.

信息熵

信息熵是对信息平均不确定性的度量,单位为比特(bit):

\[H(X)=-\sum_{x\in X} P(x)\log_2(P(x)) \]

信息量使通信领域中信息含量的概念,\(I=-\log_2 m\),其中m表示事件发生的概率,如m=0.5则信息量为 1 bit.而熵源自物理学中对热力学系统无序程度的度量.
等概率时熵最大：当X集合中各个元素的发生概率相等时熵最大.

平均互信息:得知特征Y的信息而使得对X的信息的不确定性减少的程度:

\[I(X;Y)=\sum_{x\in X,y\in Y} P(x,y)\log\frac{P(x,y)}{P(x)P(y)} \]

ID3归纳算法-(信息增益)

输入: 样本集合D, 属性集合A.
计算所有属性的信息获取量(Information Gain,信息增益):

\[\text{Gain}(D,A)=H(D)-H(D|A) \]

表示通过属性A作为节点分类增加了多少信息,即为训练数据集D和特征A的互信息.

在决策树的每一层中选择属性时选择信息增益最大的那个属性,将属性相同的样本划分到同一子类样本.重复划分过程直到:

• 给定结点的所有样本属于同一类。
• 没有剩余属性可以用来进一步划分样本。在此情况下，使用多数表决.

ID3 是贪心算法递归思想，优点是分类规则易于理解. 缺点有:

• ID3只能处理离散型数据，无法处理连续性数据。
• 无法处理缺失值。
• 选择属性时偏向选择取值多的属性（取值越多，不确定性越强，选择这个属性之后的子树变得更加确定）。比如一个变量有2个值，各为1/2，另一个变量为3个值，各为1/3，其实他们都是完全不确定的变量，但是取3个值的比取2个值的信息增益大。

C4.5-(信息增益率)

C4.5 是 J.Ross Quinlan 对 ID3 算法的改进.

1. 用信息增益率选择属性,克服 ID3 算法选择属性时偏向选择取值多的属性的缺点.
   信息增益率:信息增益与特征熵的比值, gr(D,A) = Gain(D,A) / H(A)
   H(A)为特征熵: \(H(A) = -\sum\limits_{i=1}^{n}\frac{|D_i|}{|D|}\log_2\frac{|D_i|}{|D|}\)
   特征数越多的特征对应的特征熵越大，它作为分母，可以校正信息增益容易偏向于取值较多的特征的问题。
2. 能够对连续属性进行离散化处理.
   将所有样本的属性A的值排序,对相邻两元素取平均作为划分点.
3. 能够对缺失数据进行处理.
   一般的缺失值处理方式有: 如果存在缺失属性的样本对决策树的创建影响不大则可以直接去掉.也可以补充缺失值, 从已知值中概率化分布采样,最后用非缺失值的样本比例作为系数修正信息量.^[1]
4. 构造决策树的过程中进行剪枝,不考虑元素较少的节点.

缺点: 算法效率低,只适合全部放在内存中的数据集.

C4.5 奇怪的名字来源^[2]

• ID3 : "Iterative Dichotomiser 3"
• C4.5 Quinlan 似乎没有做过名字解释, 猜测因为是用C实现的代码,4.5是版本号.ID3一出来，别人二次创新，很快就占了ID4， ID5，所以他另辟蹊径，取名C4.0算法，后来的进化版为C4.5算法。

CART

分类与回归树CART(Classification and Regression Trees) 由 (L. Breiman, J. Friedman, R. Olshen, C. Stone) 提出,是一种二分递归分割的方法, 包括决策树生成和决策树剪枝两部分.
决策树剪枝用验证集对已生成的树进行剪枝并选择最优子树,用损失函数最小作为剪枝的标准.

CART 分类树-(不纯度-Gini指数)

Gini 指数:设有K个类别,样本点属于类别k的概率是 \(p_k\), 则概率分布的 Gini 指数定义为:

\[\rm{Gini}(p)=\sum_{k=1}^K p_k(1-p_k)=1-\sum_{k=1}^K p_k^2 \]

当各类概率相等时概率分布的 Gini 指数取得最大值.
对于给定的样本集合 D, 其 Gini 指数为

\[\rm{Gini}(D)=1-\sum_{k=1}^K p_k^2=1-\sum_{k=1}^K ({|C_k|\over |D|})^2 \]

根据特征值A将集合D划分为D1, D2两部分, 在特征值A的条件下,集合D的 Gini 指数为:

\[\text{Gini}(D,A)={|D_1|\over |D|}\rm{Gini}(D_1)+{|D_2|\over |D|}\rm{Gini}(D_2) \]

ID3 和 C4.5 都是基于信息论的熵模型，涉及大量的对数运算。CART使用基尼指数来代替信息增益(比),简化模型的同时也不至于完全丢失熵模型的优点. 基尼指数代表了模型的不纯度，基尼指数越小，则不纯度越低，特征越好。这和信息增益(比)是相反的。因此CART的划分标准是选择Gini指数最小的.
二分类问题中的基尼指数Gini(p)和熵之半H(p)/2以及分类误差率之间的关系曲线如下图所示，可以看出两个曲线非常接近，都可以近似地代表分类误差率.^[3]

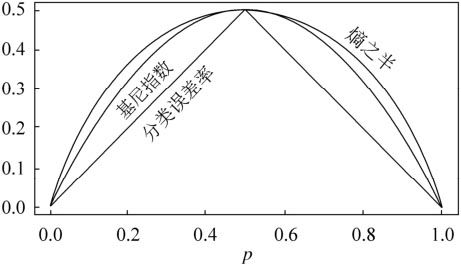
为什么会有这种关系呢?
设二分类问题中样本点属于第一个类别的概率是p,
那么概率分布的 Gini 指数等于 \(\rm{Gini}(p)=\sum_{k=1}^2 p_k(1-p_k)=2p(1-p)\).
概率分布的信息熵等于 \(H(p)=-\sum_{k=1}^2 p_k\log p_k=-p \log p-(1-p)\log (1-p)\).
将 log(p) 在 p=0.5 处泰勒展开, 得到\(\log(p)\approx \log(0.5)+\log'(0.5)\cdot (p-0.5)+O(p^2)\approx 2(p-1)\)
在 p=1 处泰勒展开, 得到\(\log(p)\approx \log(1)+\log'(1)\cdot (p-1)+O(p^2)\approx p-1\)
将 p=0.5 处泰勒展开式代入 H(p) 可得\(H(p)\approx 2\cdot \rm{Gini}(p)\).

CART 回归树(最小二乘回归树)^[4]

对于连续的目标变量,预测方法是找出一组基于树的回归方程.

1. 选择最优切分变量j与切分点s,求解
   \[\min_{j,s}[\min_{c_1}\sum_{x_i\in R_1(j,s)}(y_i-c_1)^2+\min_{c_2}\sum_{x_i\in R_2(j,s)}(y_i-c_2)^2] \]
   其中划分的区域为\(R_1(j,s)=\{x|x^{(j)}\le s\},R_2(j,s)=\{x|x^{(j)}\gt s\}\), \(c_1,c_2\)为均值\(\hat c_m={1\over N_m}\sum_{x_i\in R_m(j,s)}y_i\).
2. 对每个子区域递归调用1.

决策树对比

历史回顾：1984年提出的cart，1986年提出的ID3，1993年提出的c4.5

共同点：都是贪心算法，自上而下(Top-down approach)

ID3, C4.5, CART 三者差异:

• 回归/分类: ID3, C4.5 仅分类, CART即可分类也可回归.
• 属性选择度量方法不同：ID3 (Information Gain), C4.5 （gain ratio), CART(gini index).
• 样本数据: 特征变量的连续性/类别型: ID3只能处理类别型, 而C4.5和CART可以用于两种.
• 样本缺失值: ID3对缺失值敏感，而C4.5和CART对缺失值可以进行多种方式的处理
• 分类差别: ID3和C4.5可以多分(多叉树), 而CART是无数个二叉子节点
• 样本量考虑，小样本建议考虑c4.5、大样本建议考虑cart。c4.5处理过程中需对数据集进行多次排序，处理成本耗时较高，而cart本身是一种大样本的统计方法，小样本处理下泛化误差较大
• 特征变量使用次数: 每个特征分量在ID3和C4.5层级之间只单次使用，CART可多次重复使用
• 决策树产生过程: C4.5是通过枝剪来修正树的准确性，而CART是直接利用全部数据发现所有树的结构进行对比.

ID3算法使用的是信息增益的绝对取值，而信息增益的运算特性决定了当属性的可取值数目较多时，其信息增益的绝对值将大于取值较少的属性。这样一来，如果在决策树的初始阶段就进行过于精细的分类，其泛化能力就会受到影响，无法对真实的实例做出有效预测。
为了避免信息增益准则对多值属性的偏好，ID3算法的提出者在其基础上提出了改进版C4.5，引入了信息增益比指标作为最优划分属性的选择依据。信息增益比等于使用属性的特征熵归一化后的信息增益，而每个属性的特征熵等于按属性取值计算出的信息熵。在特征选择时，C4.5算法先从候选特征中找出信息增益高于平均水平的特征，再从中选择增益率最高的作为节点特征，这就保证了对多值属性和少值属性一视同仁。
ID3和C4.5算法都是基于信息论中熵模型的指标实现特征选择，因而涉及大量的对数计算。CART算法则用基尼系数取代了熵模型。CART分类树每次只对某个特征的值进行二分而非多分，最终生成的就是二叉树模型。

树叶剪枝

为了避免过拟合, 可以对决策树进行剪枝:

• 先剪枝
  到达一点层次后直接终止后面的分支过程,按最多数分类.
• 后剪枝
  决策树构建完毕后进行剪枝

这里介绍剪枝的通用思想, 而不介绍 CART 这种自带的剪枝算法.

1. 计算每个节点的经验熵(特征熵).
2. 递归地从树的叶节点向上回缩.
   比较回缩前与回缩后的整体树的损失函数, 如果回缩使得损失函数变小, 那么进行回缩,也就是剪枝. 其中损失函数定义为叶子节点经验熵的和与正则化项(模型复杂度)两部分.
   \(C_\alpha(T)=\sum_{t}^{|T|}N_t H_t(T)+\alpha |T|\)

通常情况下， 随机森林不需要后剪枝。
另外提高泛化能力,避免过拟合的方法是: 随机森林

优缺点

优点:直观

缺点:

• 难处理连续性变量
• 类别较多时,错误增加的比较快
• 不适合大规模数据集

实践中用 Gini 指数比较多,而 ID3 仅用于教学.

附录 - 信息公式及其属性

名称	公式	相似性?	对称性?
联合熵(Joint Info)	\(H(T,Y)=-\sum_t\sum_yp(t,y)\log_2p(t,y)\)	无法衡量	Y
互信息(Mutual Info)	\(I(T,Y)=\sum_t\sum_yp(t,y)\log_2{p(t,y)\over p(t)p(y)}\)	Y	Y
条件熵(Conditional Entropy)	\(H(Y,T)=-\sum_t\sum_yp(t,y)\log_2p(y|t)\)	N	N
交叉熵(Cross Entropy)	\(H(T;Y)=-\sum_zp_t(z)\log_2p_y{(z)}\)	N	N
KL散度(Divergence)	\(KL(T;Y)=\sum_zp_t(z)\log_2{p_t(z)\over p_y{(z)}}\)	N	N

相对熵（relative entropy）又称为KL散度（Kullback–Leibler divergence，简称KLD），信息散度（information divergence），信息增益（information gain）。

互信息（en:Mutual information）和KL散度之间的关系：

\[I(X;Y)=D_{KL}(P(X,y)\|P(X)P(Y)) \]

互信息衡量的是两个变量之间的独立性。

---

1. 决策树算法原理(上) ↩︎

2. C4.5名字来源 ↩︎

3. 决策树算法原理(下) ↩︎

4. http://www.cnblogs.com/xingshansi/p/6847334.html ↩︎