坐标下降 vs 梯度下降
梯度下降与坐标下降优化方法
梯度下降法:
在每次迭代更新时选择负梯度方向(最速下降的方向)进行一次更新.不断迭代直至到达我们的目标或者满意为止.
坐标下降法:
坐标下降法属于一种非梯度优化的方法，它在每步迭代中沿一个坐标的方向进行搜索，通过循环使用不同的坐标方法来达到目标函数的局部极小值。求导时只对一个维度(坐标轴方向)进行求导,而固定其它维度,这样每次只优化一个分量.
相比梯度下降法而言，坐标下降法不需要计算目标函数的梯度，在每步迭代中仅需求解一维搜索问题，所以对于某些复杂的问题计算较为简便。但如果目标函数不平滑的话，坐标下降法可能会陷入非驻点。为了加速收敛，可以采用一个适当的坐标系，例如通过主成分分析获得一个坐标间尽可能不相互关联的新坐标系（参考自适应坐标下降法）。[1]
平滑与非平滑的函数示例如下图:
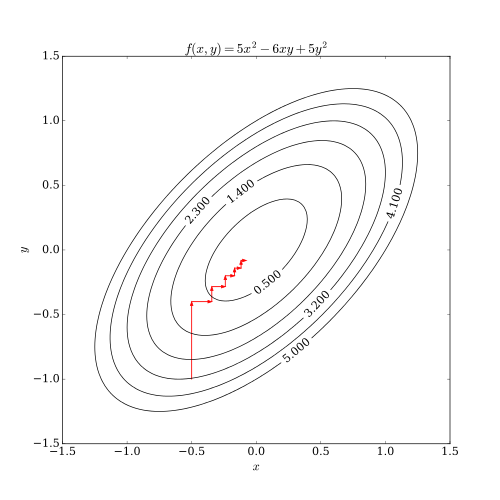
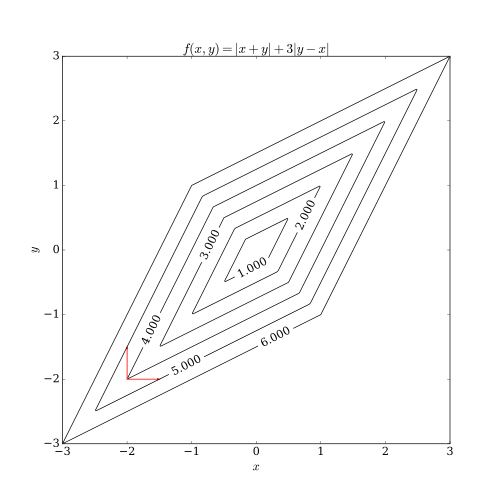
注意事项
关于坐标下降法，有几点需要注意的：
1.坐标下降的顺序是任意的。
2.坐标下降的关键在于一次一个地更新，所有的一起更新有可能会导致不收敛。
3.坐标上升法和坐标下降法的本质一样，只不过目标函数成为求极大值了。
对比
与通过梯度获取最速下降的方向不同，在坐标下降法中，优化方向从算法一开始就予以固定。例如，可以选择线性空间的一组基 \(( e_1, e_2,\dots ,e_n)\)作为搜索方向。 在算法中，循环最小化各个坐标方向上的目标函数值。
期望最大化算法(EM)
可以理解为坐标上升法。
含有隐变量对数似然求导比较复杂，因此先固定参数求隐变量后验分布(E步)，然后固定隐变量求参数(M步)，交替进行。
这里也来说明一下二阶优化方法:
二阶优化方法
- 二阶优化方法可以用到深度学习网络中，比如DistBelief，《Large-scale L-BFGS using MapReduce》.采用了数据并行的方法解决了海量数据下L-BFGS算法的可用性问题。
- 二阶优化方法目前还不适用于深度学习训练中，主要存在问题是： 1. 最重要的问题是二阶方法的计算量大，训练较慢。 2. 求导不易，实现比SGD这类一阶方法复杂。 3. 另外其优点在深度学习中无法展现出来，主要是二阶方法能够更快地求得更高精度的解，这在浅层模型是有益的，但是在神经网络这类深层模型中对参数的精度要求不高，相反 相对而言不高的精度对模型还有益处，能够提高模型的泛化能力。 当然，二阶优化方法也有优点，在凸优化中，训练较SGD这类方法更为稳定更为平滑，不用调参[2]
应用
现在的机器学习和深度学习方法几乎清一色的使用梯度下降方法,比如SGD应用很广泛. 但是坐标下降法也有其用武之地. 比如LASSO回归系数的计算, SVM对偶问题的优化算法SMO.
本文源自http://www.cnblogs.com/makefile/
