生成式模型之 GAN

生成对抗网络（Generative Adversarial Networks，GANs），由2014年还在蒙特利尔读博士的Ian Goodfellow引入深度学习领域。2016年，GANs热潮席卷AI领域顶级会议，从ICLR到NIPS，大量高质量论文被发表和探讨。Yann LeCun曾评价GANs是“20年来机器学习领域最酷的想法”。

Generative Adversarial Nets(GAN)

Generative Adversarial Networks论文提出了一种通过对抗过程来评估生成模型。其训练两个模型：仿照原始数据分布生成数据的模型G和评估数据来源（原始数据/生成数据）的模型D。训练G的目标是最大化D犯错的概率，训练D的目标是最大化区分真实训练样本与G生成的样本的能力。

如果能够知道训练样本的分布\(p(x)\)，那么就可以在分布中随机采样得到新样本，大部分的生成式模型都采用这种思路，GAN则是在学习从随机变量z到训练样本x的映射关系，其中随机变量可以选择服从正太分布，那么就能得到一个由多层感知机组成的生成网络\(G(z;\theta_g)\)，网络的输入是一个一维的随机变量，输出是一张图片。

GAN的优化是一个极小极大博弈问题，公式如下：

\[\underset{G}{\min} \: \underset{D}{\max}V(D,G) =\mathbb E_{x\sim p_{data}(x)}[logD(x)]+\mathbb E_{z\sim p_{z}(z)}[log(1-D(G(z)))] \]

优化这个函数，使\(p_z(x)\)接近\(p_{data}\).下面首先去掉期望符号：

\[\begin{align} V(G,D)&=\int_x p_{data}(x)\log(D(x))dx+\int_zp_z(z)\log(1-D(g(z)))dz \\ &=\int_x [p_{data}(x)\log(D(x))+p_g(x)\log(1-D(x))]dx \end{align} \]

先固定G，求\(\underset{D}{\max}V(D,G)\),令其导数等于0，求得D的最优解

\[D^*_G(x)={p_{data}(x)\over p_{data}(x)+p_g(x)} \]

现在固定D，优化G：将\(D^*_G\)带入目标函数。

\[\begin{align} \underset{G}\min V(G,D^*_G) &= \int_x [p_{data}(x)\log{p_{data}(x)\over p_{data}(x)+p_g(x)}+p_g(x)\log{p_g(x)\over p_{data}(x)+p_g(x)}]dx \\ &= \mathbb E_{x\sim p_{data}}[\log{p_{data}(x)\over p_{data}(x)+p_g(x)}]+\mathbb E_{x\sim p_g}[\log{p_g(x)\over p_{data}(x)+p_g(x)}] \\ &= -\log 4+KL(p_{data}\|{p_{data}+p_g\over 2})+KL(p_g\|{p_{data}+p_g\over 2}) \\ &= -\log 4+2JS(p_{data}\|p_g) \end{align} \]

其中KL散度：\(KL(P\|Q)=\mathbb E_{x\sim P}\log{P\over Q}=\int_xP(x)\log{P(x)\over Q(x)}dx\)

JS散度：\(JS(P\|Q)={1\over 2}KL(P\|{P+Q\over 2})+{1\over 2}KL(Q\|{P+Q\over 2})\)

JS散度具有对称性，而KL没有。

只要P和Q没有一点重叠或者重叠部分可忽略，JS散度就固定是常数，而这对于梯度下降方法意味着——梯度为0！此时对于最优判别器来说，生成器得不到梯度信息；即使对于接近最优的判别器来说，生成器也有很大机会面临梯度消失的问题。

参考 WGAN的介绍。

f-GAN

在GAN中可以使用任意的f-divergency,相关论文f-GAN(Sebastian Nowozin, Botond Cseke, Ryota Tomioka, “f-GAN: Training Generative Neural Samplers using Variational Divergence Minimization”, NIPS, 2016)

f-divergence

P和Q是两个分布,p(x),q(x)是x的分布概率

\[D_f(P||Q)=\int_x q(x)f({p(x)\over q(x)})dx \]

其中f是凸函数且f(1)=0,\(D_f(P||Q)\)衡量了P和Q之间的距离.

当\(\forall x,p(x)=q(x)\)时,\(D_f(P||Q)\)具有最小值0.

当\(f(x)=x\log x\)时,\(D_f(P||Q)=\int_xp(x)\log({p(x)\over q(x)})dx\),即KL divergence.

当\(f(x)=-\log x\)时,\(D_f(P||Q)=\int_xq(x)\log({q(x)\over p(x)})dx\),即reverse KL divergence.

当\(f(x)=(x-1)^2\)时,\(D_f(P||Q)=\int_x{(p(x)-q(x))^2\over q(x)}dx\)为Chi Square divergence.

Fenchel Conjugate

每个凸函数f都有一个与之相对的conjugate function f*:

\(f^* (t)=\max_{x\in dom(f)}\{xt-f(x)\}\),且(f *) * = f.

\(f(x)=\max_{t\in dom(f^*)}\{xt-f^*(t)\}\),带入\(D_f(P||Q)\)得:

\[\begin{align} D_f(P||Q) &=\int_x q(x)f({p(x)\over q(x)})dx \\ &=\int_xq(x)(\max_{t\in dom(f^*)}\{{p(x)\over q(x)}t-f^*(t)\})dx \\ &=\max_D\int_x p(x)D(x)dx-\int_x q(x)f^*(D(x))dx \\ &\text{(t=D(x))} \end{align} \]

因此GAN中

\[D_f(P_{data}\|P_G)=\max_D\{E_{x\sim P_{data}}[D(x)]-E_{x\sim P_G}[f^*(D(x))]\} \]

可以使用任何的f-divergence,如JS,Jeffrey,Pearson.

WGAN

原始版本:weight clipping,改进版本:gradient penalty.

论文:

• Martin Arjovsky, Soumith Chintala, Léon Bottou, Wasserstein GAN, arXiv preprint, 2017
• Ishaan Gulrajani, Faruk Ahmed, Martin Arjovsky, Vincent Dumoulin, Aaron Courville,“Improved Training of Wasserstein GANs”, arXiv preprint, 2017

主要思想:使用Earth Mover's Distance(Wasserstein Distance)来评估两个分布之间的距离.推土机距离表示将一个分布搬运变为另一个分布的最小搬运的量.

之前GAN所采用的JS divergence的缺点是当两个分布没有交集时,距离是0,梯度为0,网络很难学习.Earth Mover's Distance便可以解决这个问题.此时网络能够持续学习,但为了防止梯度爆炸,需要weight clipping等手段.

对抗样本(adversarial examples)

14年的时候Szegedy在研究神经网络的性质时，发现针对一个已经训练好的分类模型，将训练集中样本做一些细微的改变会导致模型给出一个错误的分类结果，这种虽然发生扰动但是人眼可能识别不出来，并且会导致误分类的样本被称为对抗样本，他们利用这样的样本发明了对抗训练(adversarial training)，模型既训练正常的样本也训练这种自己造的对抗样本，从而改进模型的泛化能力[1]。如下图所示，在未加扰动之前，模型认为输入图片有57.7%的概率为熊猫，但是加了之后，人眼看着好像没有发生改变，但是模型却认为有99.3%的可能是长臂猿。

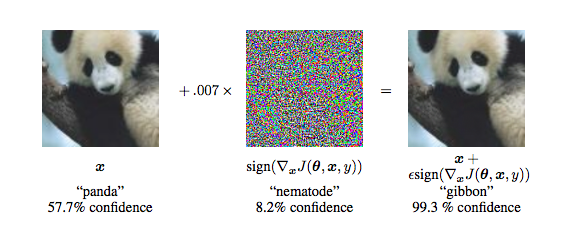
对抗样本跟生成式对抗网络没有直接的关系，对抗网络是想学样本的内在表达从而能够生成新的样本，但是有对抗样本的存在在一定程度上说明了模型并没有学习到数据的一些内部表达或者分布，而可能是学习到一些特定的模式足够完成分类或者回归的目标而已。

GAN生成的图片能否用于CNN训练？

现在来说，应当不可以。由于GAN是从较小的分布中采样生成的，是真实世界的极小的一部分，所以拿来训练没有广泛的适用性。另外，当前的GAN生成较大的图片比较困难（32x32以上）。

参考资料

• GAN作者Ian Goodfellow的教程论文NIPS 2016 Tutorial: Generative Adversarial Networks
• 台大李宏毅 deep learning tutorial
• 简述生成式对抗网络